うなりとは

音には「うなり」という現象があります。
日常生活で「うなり」を聞くことは滅多にないと思うので、実感はないかもしれません。
しかし、私たちの耳は高品質(？)なので、実際に聞いてみると「うなり」を実感することができます。

今回は、「うなり」とは何なのかについて、わかりやすく簡単に解説をしていきます。

うなりとは

うなりとは、振動数が少し違う2つの音を同時に聞くと「ワーン、ワーン」と聞こえる現象のことをいいます。

今回は、実際に音を聴いてみましょう。

まず、これが440Hzの音です。「ラ」の音ですね。
(「ラ」以外の音は振動数が無理数なので、こういう場合は「ラ」の音しか出てこない)

こちらの音は442Hzです。オーケストラでは「ラ」の音を440Hzではなく442Hzに合わせることが多いです。

この2つの音はよく似ているため、2つの音を聴き比べても、音の違いはあまりよく分かりませんよね。
しかし、この2つの音を同時に聴くと、不思議なことに「うなり」という現象を聞くことができます。

この音は、440Hzと442Hzの音を同時に流したものです。
確かに、「ワーン、ワーン」と聞こえてきますよね。

一体なぜ、「うなり」という現象が起こるのでしょうか？

うなりの仕組みと公式

うなりの仕組みは意外にも単純です。

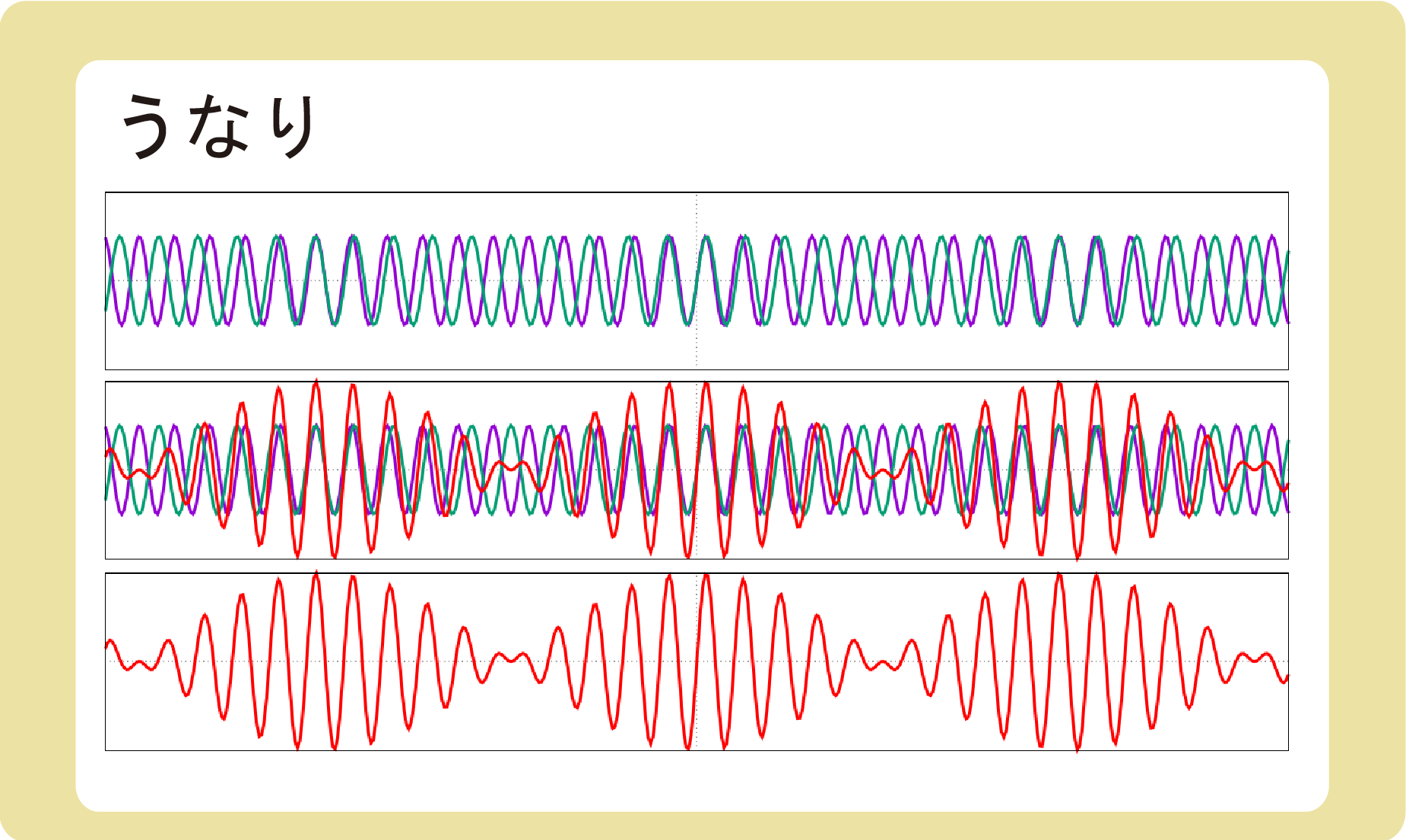
図のように、振動数が少しだけ異なる緑の波と紫の波があるとします。
この2つの波は振動数が少しだけ異なるので、時間が経つと波の位相がズレていきます。
(つまり、このグラフはy-tグラフであるということです)

この2つの波を重ね合わせた波が、赤色の波です。赤色の波が大きくなったり小さくなったりするため、私たちは「ワーン。ワーン」とうなりを聞くことになります。

振動数の差が大きいと波がズレるのも早くなるため、1秒あたりに聞こえるうなりの数が多くなります。

上から順番に、

・440Hzと441Hz
・440Hzと445Hz
・440Hzと450Hz

の音を同時に流した音になります。
確かに、振動数の差が大きいほど、うなりの回数も多くなっていますよね。

従って、うなりの公式は

$$f=|f_1-f_2|$$

(f：1秒間に聞こえるうなりの数［回/s］　f₁, f₂：2つの振動数)

という式で表されます。

絶対値が付いていますが、うなりの回数はマイナスにならないという意味です。
要は2つの振動数の差が1秒当たりのうなりの数であるということだけ分かっていれば大丈夫です。

例題

振動数が440HzのおんさA、振動数が435HzのおんさB、振動数の分からないおんさCがある。おんさAとおんさCを同時に鳴らすと、毎秒2回のうなりが生じ、おんさBとおんさCを同時に鳴らすと、毎秒3回のうなりを生じた。おんさCの振動数は何Hzか。

まとめ

振動数が近い2つの音を同時に聴くと「うなり」という現象が聞こえます。
公式は\(f=|f_1-f_2|\)という、引き算をするだけの式なので、物理基礎ではあまり難しい問題は出題されません。

物理では、ドップラー効果の範囲で急に出てきたり、三角関数の和積を使って公式を求めたりする問題が出てきますが、引き算をするだけなのであまり難しくはないですね。

 

次の内容はこちら

一覧に戻る