・合成速度とは何か
・相対速度とは何か
今回は速度の合成(合成速度)と相対速度についての解説をしていきます。
この2つはそれぞれ別の内容なのですが、一緒に習うことが多いです。
考え方は非常に簡単ですので、しっかり勉強しましょう。
合成速度とは
速度を合成したもの。
例)「エスカレーターの上では速く動ける」
$$v=v_1+v_2$$
エスカレーターの上を歩くと早く動ける、流れている川を泳いで下ったら早く泳げる、このように何かの上で物体が動くと速度が合成される、ということを合成速度と言います。
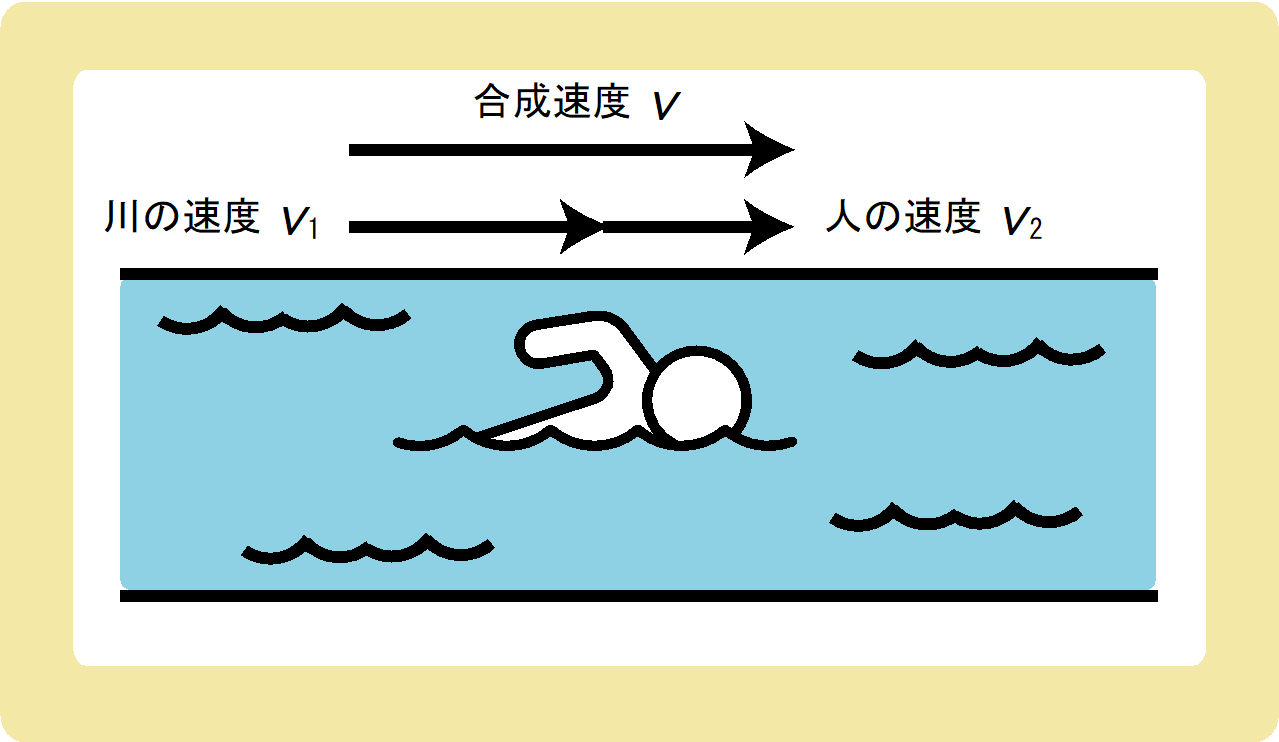
速度の合成の考え方や公式は非常に簡単で、ただ足し算をするだけです。
$$v=v_1+v_2$$
合成速度はただの足し算なので、v1とv2の順番はどちらでも構いません。
(人の速度を必ずv1にする必要などはありません。)
例題
例題1
静水であれば1m/sの速さで泳げる人(流れのない水であれば1m/sの速さで泳ぐことができる人)が、水の流れの速さが3m/sの川を泳いで下っている。
陸にいる人から見ると、この川を泳ぐ人の速さは何m/sか。
“”速度””の合成ということは、速さだけでなく向きも考えないといけないので、どちら向きなのかということに気を付けないといけません。
先程の例題は川の流れと人の泳ぐ方向が同じでしたが、2つの向きが逆の場合もあります。
(物理基礎では同じ向きか逆向きを考えますが、物理では斜め向きの合成速度を考えます。)
速さではなく速度を聞かれた場合は「向き」も答えましょう。
例題2
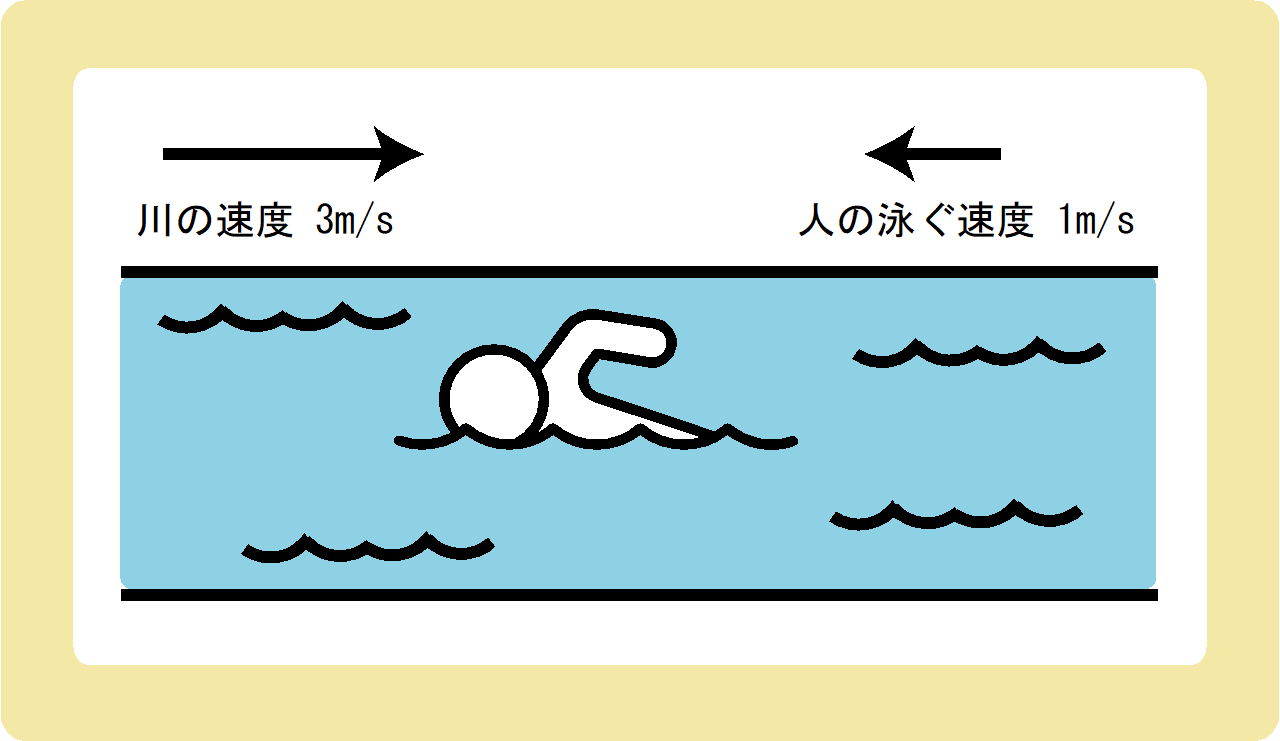
東向きに3m/sの速さで流れる川を、静水であれば1m/sの速さで泳げる人が西向きに泳いでいる。陸にいる人から見ると、この川を泳ぐ人の速度は何m/sか。
相対速度とは
ある観測者から見たときの速度。
例)「電車と電車がすれ違うと速く感じる」「自転車から見たら車が遅く見える」
$$v_{AB}=v_B-v_A$$
相対速度とは「ある観測者から見たときの速度」のことを言います。
簡単に言うと「動いている人から見たときの物体の速度」のことです。
普段、物体の速さは「静止している地面から」見ますが(この場合、わざわざ相対速度という言葉をあまり使いません)、私たちは車や電車に乗りながら景色を見ますし、歩きながら誰かが動いているのを見ることも多いです。
このように、「動いている人から見たときの物体の速度」を考えよう、ということが相対速度の内容になります。
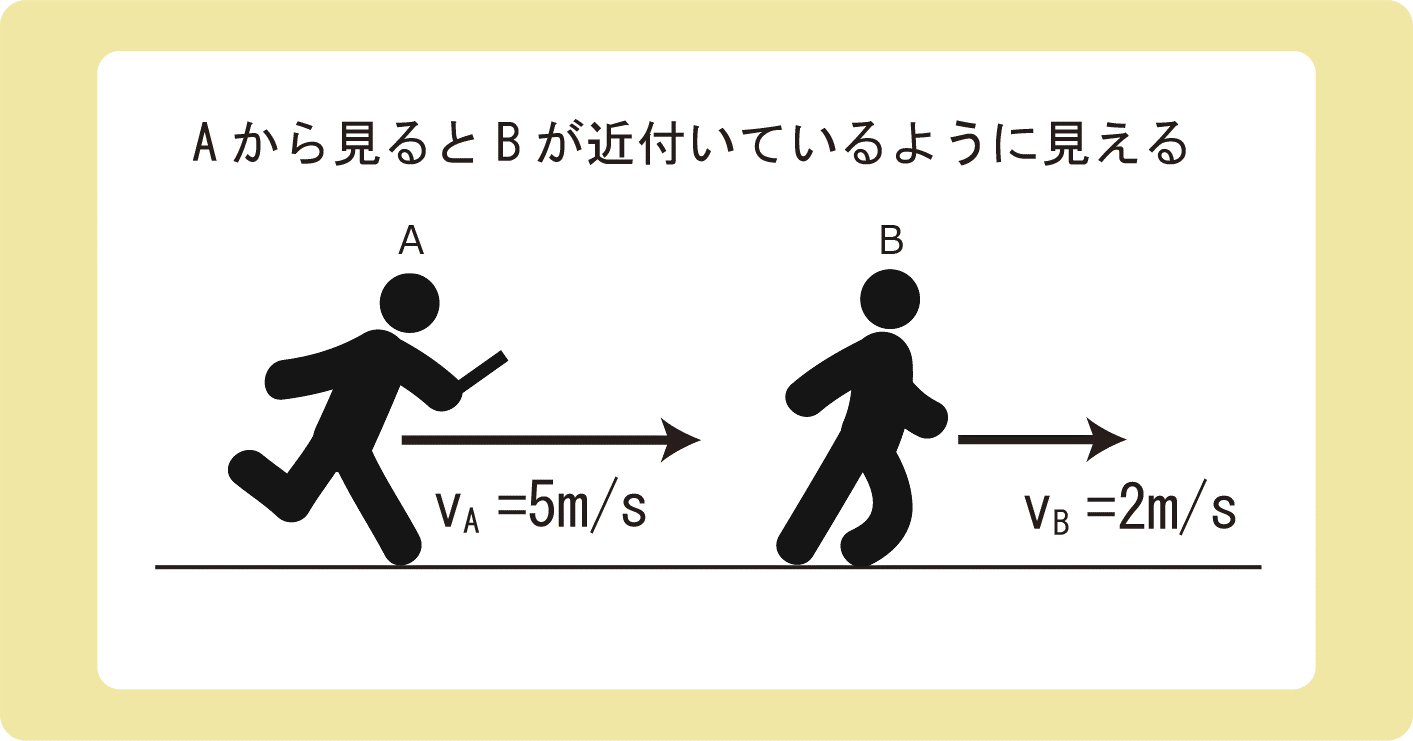
例えば、一直線上を走っているAさんとBさんがいるとします。
地面から見たAさんの速度は5m/s、Bさんの速度は2m/sです。
AさんとBさんは両方とも右向きに進んでいるのですが、AさんとBさんの速さの差は3m/sなので、Aさんから見るとBさんが3m/sで近付いているように見えます。
公式\(v_{AB}=v_B-v_A\)を使うと
$$v_{AB}=2-5\\
v_{AB}=-3$$
∴左向きに3m/s
で近づいてくるという計算になります。
(※右向きを正としています)
vABとは「Aに対するBの相対速度」(「Aから見たBの速度」)のことであり、見ている方をA、見られている方をBにしないといけません。
相対速度は引き算なので、順番が逆になると計算結果も変わってしまいます。合成速度とは違って順番を間違えないようにしましょう。
例題
例題3

同一直線上を赤い車と青い車が進んでいる。赤い車が右向きに50km/h、青い車は左向きに50km/hの速さで進んでいるとき、赤い車に対する青い車の相対速度を求めなさい。
例題4
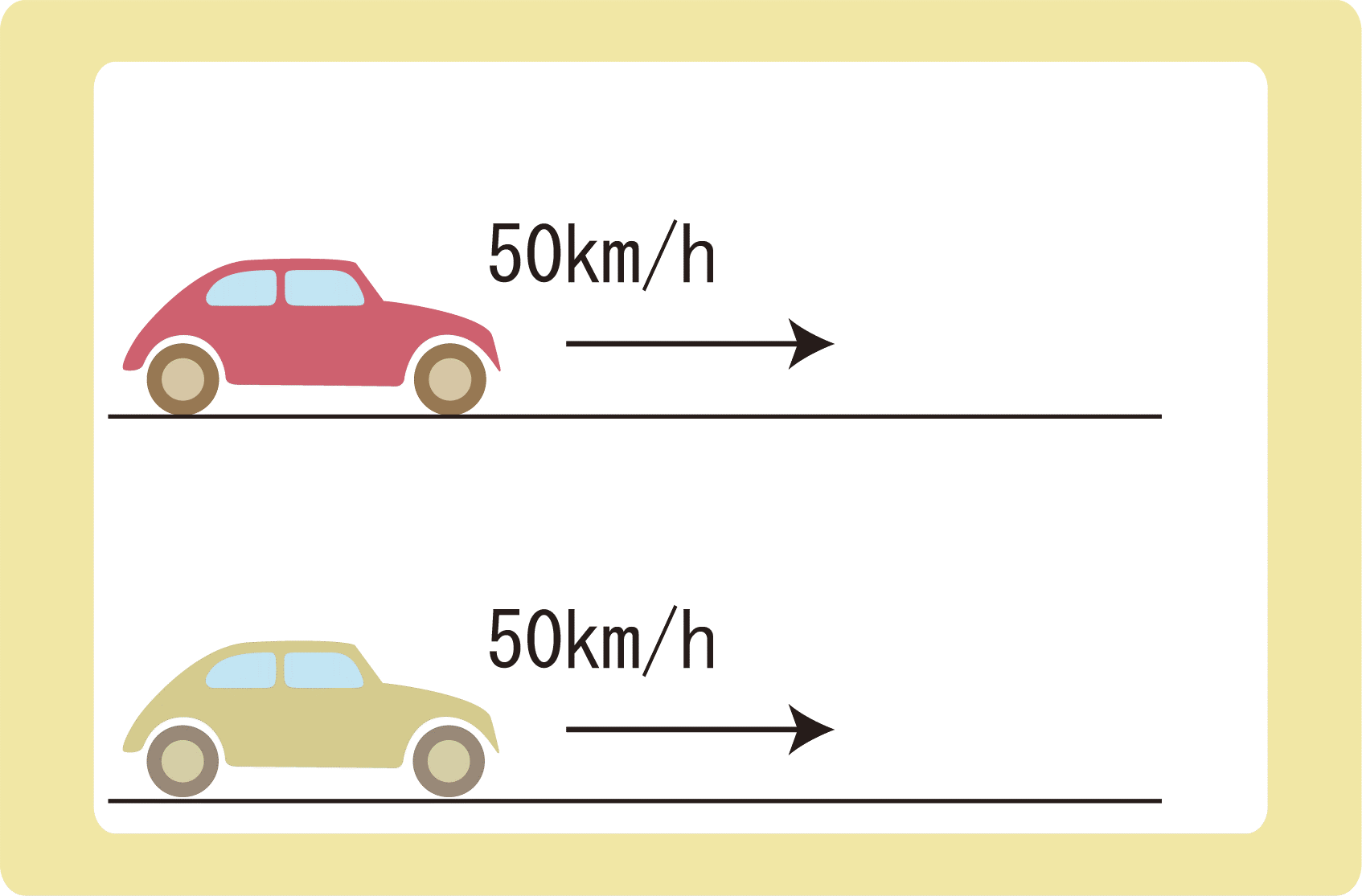
右向きに50km/hの速さで走っている赤い車と同じ向きに、黄色い車が50km/hで走っている。赤い車に対する黄色い車の速度を求めなさい。
例題5
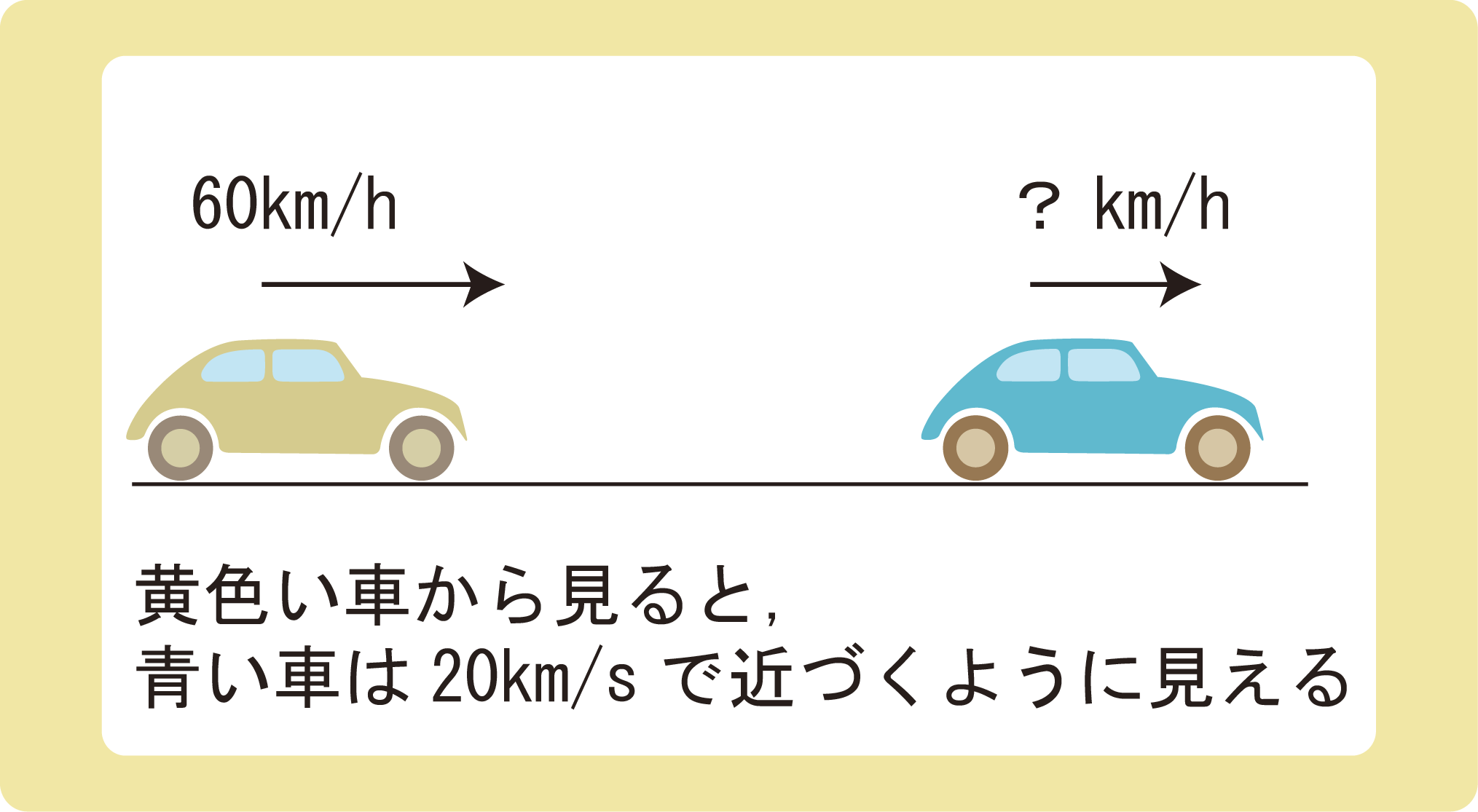
同一直線上を黄色い車と青い車が走っている。黄色い車が右向きに60km/hで走っており、黄色い車から見ると、黄色い車の前方にある青い車が20km/hで近付いているように見えた。このとき、青い車の速度を求めなさい。
まとめ
合成速度は「エスカレーターの上を歩く」「川の上を船が進む」のような、速度を合成するものであり、公式は
$$v=v_1+v_2$$
になります。
一方、相対速度は「車から見た別の車の運動」「電車の中から見た雨の動き」のような、動いている観測者から見る物体の速度のことで、公式は
$$v_{AB}=v_B-v_A$$
となります。
2つは名前が似ているので混同しないように注意しましょうね。
応用として縦横斜めの合成速度と相対速度もありますが、詳しくは物理の方で勉強することになります。












