・加速度とは何か
・加速度の公式の導出と、問題の解き方
・加速度のグラフの考え方
物理基礎を習う前までは、物体の運動を等速直線運動として扱うことが普通でした。
しかし、物体の運動は早くなったり遅くなったりするのが普通です。
物理では、物体が速くなることを「加速」と言います。
今回は、物体が速くなる運動(加速運動)について、可能な限りわかりやすく簡単に解説を行いたいと思います。
加速度とは
単位時間あたりの速度変化。つまり、1秒でどれくらい速く(遅く)なったか。
記号は「a」、単位は[m/s2]
加速度とは「単位時間あたりの速度変化」のことであり、aという記号を使います。
単位は［m/s2］(メートル毎秒毎秒)です。
加速度を簡単に説明すると、1秒でどれくらい速くなったか、という意味です。
なお、遅くなることは減速と言わず、負の加速(加速度がマイナス)と言います。
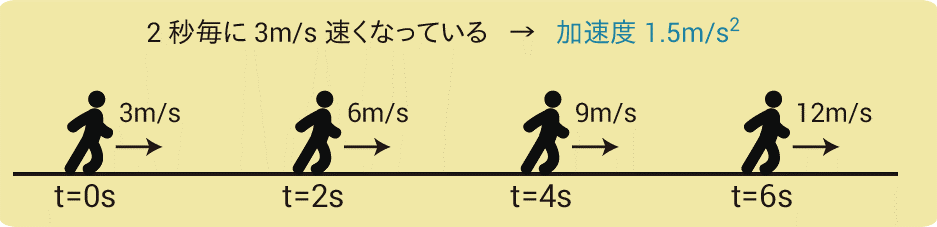
例えば、2秒毎に速さが3m/sずつ速くなっている人がいたとします。
加速度とは「1秒でどれくらい速くなった」のことを言うため、この人の加速度はa=1.5m/s2となります。
どのように計算したかと言うと、
$$3÷2=1.5$$
というふうに計算しています。
1秒あたり、どれくらい速度が変化したか、なので、速度を時間で割っているということですね。(分数よりも少数で表すことが多いです。分数が間違いというわけではありません。)
ちなみに、速度[m/s]を時間[s]で割っているため、
$$m/s÷s=m/s^2$$
という単位になっています。
m/sの「 / 」の部分は分数のように考えることができるので、
$$\frac{m}{s}÷s=\frac{m}{s^2} $$
と考えることができます。
このとき、
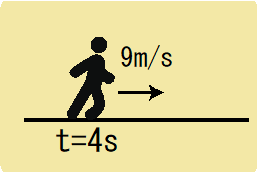
この図のように、運動の一部だけを見て
$$9÷4=…$$
のように計算してはいけません。
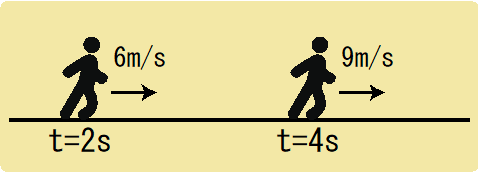
運動のある2つの部分を見比べて、「2秒で3m/s速くなった！」ということを確認しなければならないのです。
加速度aを求める計算式は
$$a=\frac{9-6}{4-2}\\
=\frac{3}{2}\\
=1.5$$
となるので、
公式としては
$$a=\frac{v_2-v_1}{t_2-t_1}=\frac{Δv}{Δt}$$
と表されますが、正直あまり使わない公式なので分からなくても問題は解けます。
（Δ(でるた)：変化を表す Δv：速度変化 Δt：時間変化 という意味になる）
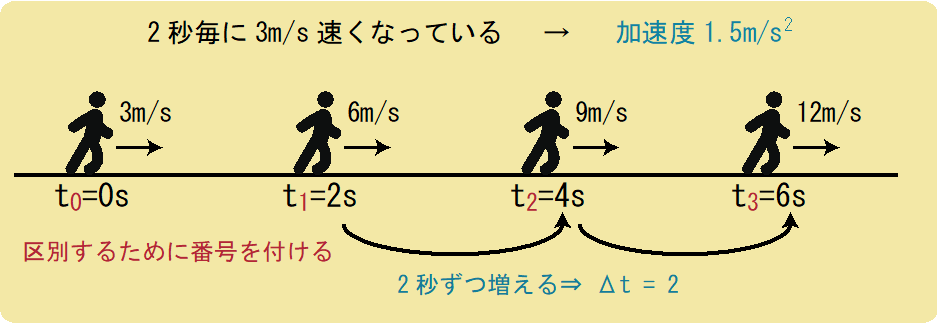
今回のように、速度や時間が複数回登場している場合は、t1やt2のように右下に数字を付けることで区別をします。
特に、最初の(t=0秒のとき、つまりスタート地点の)vのことをv0と表し、初速度と言います。
ｖはただの速度、v0は初速度（最初の速度）と区別することが多いですね。
ちなみに、読み方は「ぶいおー」ではなく「ぶいぜろ」です。0秒のときのｖなので「ぶいぜろ」。
（これを読んでる貴方も数日後にはきっとv0を「ぶいおー」と読んでいると思いますが、計算に影響はないのでそれでもいいです。）
なお、本来であれば、このような加速度のことを平均の加速度と言い、瞬間の加速度とは区別して考えるのですが、あまり気にせず、どちらも共通して「加速度」と呼んでいます。
このように、加速度が一定である直線上の運動のことを等加速度直線運動と言います。
加速度とグラフ
等加速度直線運動では
傾き⇒加速度a
面積⇒距離x
この加速度運動をv-tグラフにしてみましょう。
v-tグラフとは、縦軸が速度ｖ、横軸が時間tのグラフのことです。
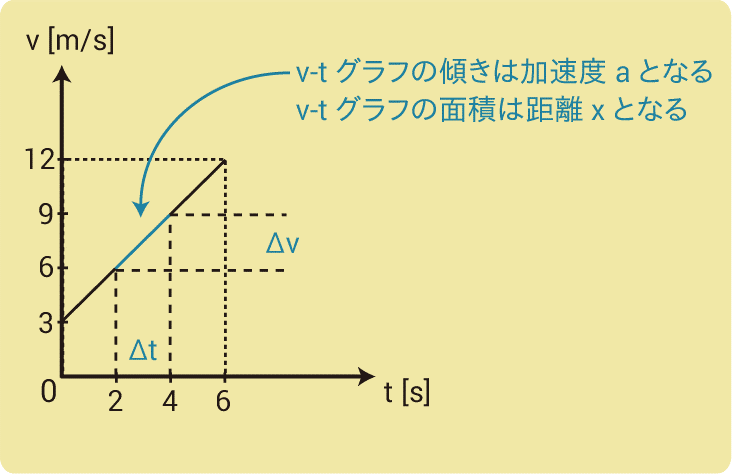
等速直線運動では速さが変わらない真横のグラフでしたが、等加速度直線運動は速さが増えているので右上がりのグラフになります。
(もちろん、遅くなっているときは右下がりのグラフです。)
このとき、v-tグラフでは傾きが加速度aとなり、等速直線運動のときと同様に、グラフと軸で囲まれた面積が距離ｘとなります。
等速直線運動のv-tグラフが真横なのは、傾いていない＝加速度が0＝等速ということですね。
等加速度直線運動の公式の導出
等加速度直線運動の3公式
$$①v=v_0+at\\
②x=v_0t+\frac{1}{2}at^2\\
③v^2-{v_0}^2=2ax$$
次に、文字だけでもう一度加速度について考えてみます。
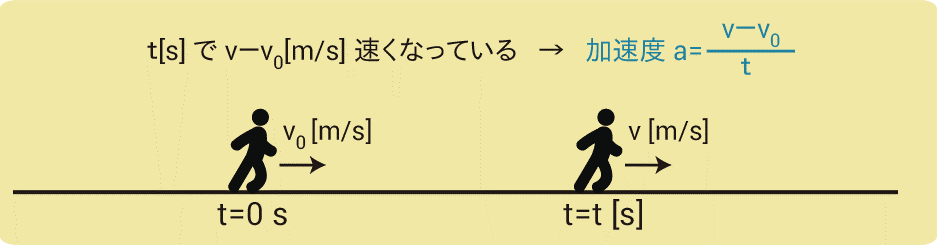
初速度v0 [m/s]の人がt[s]で速度v[m/s]になる場合を考えましょう。
加速度は単位時間あたりの速度変化のことなので、先程の公式に当てはめると、$$a=\frac{v-v_0}{t}$$となります。
この式をさらに変形をすると、$$①v=v_0+at$$という式ができますね。
数字で考えたときと同様にv-tグラフを考えましょう。
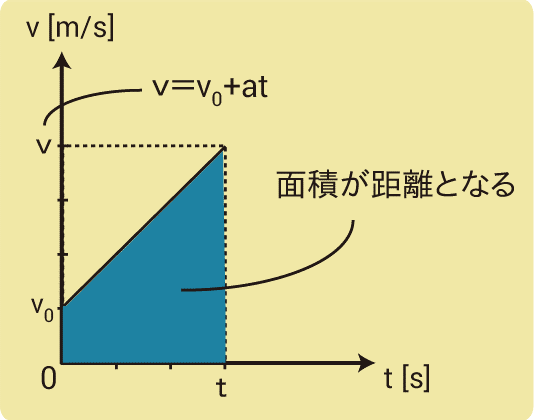
この運動が等加速度直線運動だと考えると、グラフは数字で考えたときと同じ形になります。
(分かりやすさのため、加速度はプラスとします)
ここで、グラフと軸で囲まれた面積が距離ｘとなるのを利用して面積を求めてみましょう。
青色の部分を横から見ると台形に見えるので、
x=(v_0+v)×t×\frac{1}{2}$$
となります。
ここに\(v=v_0+at\)を代入すると
$$x=(v_0+v_0+at)×t×\frac{1}{2}$$
となり、展開すると
$$②x=v_0t+\frac{1}{2}at^2$$
となります。
最後に、
\begin{cases}
v=v_0+at &…①\\
x=v_0t+\frac{1}{2}at^2 &…②
\end{cases}
を連立して t を削除すると3つ目の公式が出てきます。
(①をt=… の形に式変形して、そのtを②に代入するという意味です)
①より
$$t=\frac{v-v_0}{a}$$
を②に代入
$$x=v_0×\frac{v-v_0}{a}+\frac{1}{2}×a×(\frac{v-v_0}{a})^2\\
x=\frac{v_0v-{v_0}^2}{a}+\frac{v^2-2v_0v-{v_0}^2}{2a}\\
x=\frac{v^2-{v_0}^2}{2a}$$
$$③v^2-{v_0}^2=2ax$$
と公式を導きだせます。
この3つの式のことを等加速度直線の3公式といい、よく使う重要な公式となっています。とりあえず、この3つの公式を使いこなせれば、定期試験での赤点はないでしょう。
加速度の問題はこの3つの公式を使うのですが、最初の頃はどの公式を使えばいいか分からない人が多いと思います。
$$①v=v_0+at\\
②x=v_0t+\frac{1}{2}at^2\\
③v^2-{v_0}^2=2ax$$
①の式は、時間tと速度vがあるときに用いる
②の式は、時間tと変位（距離）xがあるときに用いる
③の式は、時間tが全く出てこないときに用いる
また、必ず正の向きを決めてから公式を用いる必要があります。（右向きを正とするなら左向きはマイナスとなる）
問題を多く解き、公式の扱いに慣れていきましょう。
例題
例題1
初速度3m/sで右方向に進んでいた物体が一定の加速度で加速し、2秒後に速さが右方向に15m/sになった。
（1）物体の加速度は何m/s2か。
（2）2秒間で何ｍの距離を進むか。
例題2
東向きに6m/sで運動していた物体が、等加速度運動をして、3ｓ後に西向きに速さ18m/sとなった。
(1)この物体の加速度はどちら向きに何m/s2か。
(2)この10秒間における変位は何mか。
例題3
右向きに15m/sで走行していた物体が等加速度直線運動をして、100ｍ移動したあとに、右向きに25m/sになった。この自動車の加速度は何m/s2になるか。
例題4
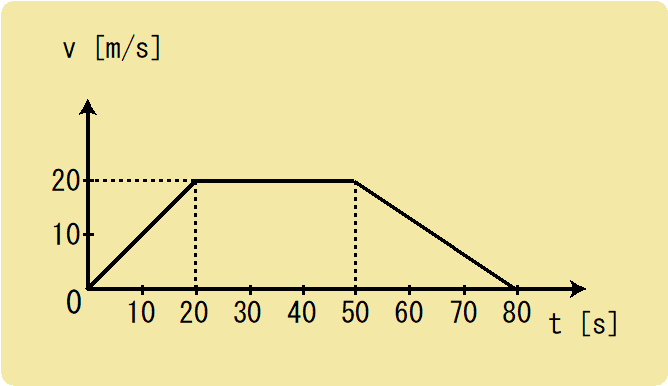
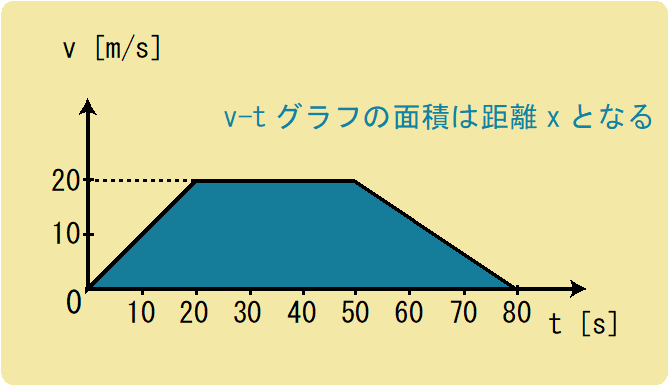
この図は、直線上を運動するある物体のｖ－ｔグラフです。物体の進行方向を正の向きとして、次の問いに答えなさい。
(1)
(i) t＝0～20ｓにおける加速度a1は何m/s2か。
(ii) t＝20～50ｓにおける加速度a2は何m/s2か。
(iii) t＝50～80ｓにおける加速度a3は何m/s2か。
(2) 80秒間に進んだ距離は何ｍか。
v-tグラフにおいて、傾きが加速度になるということを用います。
傾きとは、\(\frac{どれくらい上に増えたか}{どれくらい右に進んだか}\)であるため
(i)
$$a_1=\frac{20}{20}=1$$
∴1m/s2
(ii)
$$a_2=\frac{0}{30}=0$$
∴0m/s2
※そもそも、グラフが傾いていないので等速⇒加速度は0ということと考えても大丈夫です。
(iii)
$$a_3=\frac{-20}{30}=-\frac{2}{3}$$
\(∴-\frac{2}{3} m/s^2\)
(2)v-tグラフにおいて、面積が進んだ距離となるので、
$$台形の面積S=(上底+下底)×高さ×\frac{1}{2}$$
を使うと
$$x=(30+80)×\frac{1}{2}\\
x=1100m$$
∴1100m
となります。
まとめ
加速度とは、1秒でどれくらい速く(遅く)なったかのことで、記号はaで単位は［m/s2］です。
等加速度直線運動の3公式
$$①v=v_0+at$$
$$②x=v_0t+\frac{1}{2}at^2$$
$$③v^2-{v_0}^2=2ax$$
この3つの公式をどれくらい使いこなせるかが、加速度の問題を解けるかどうかのポイントになっています。
数多くの問題を解くことが、加速度の問題を解くことができる近道であるため、ここにある例題以外の問題もたくさん解くことをオススメします。
以上で加速度の説明とさせていただきます。
