弦の固有振動とは

前回は、どんな物体にも「固有振動」というものが存在している、という話をしました。
机やスマホを叩くといつも同じ音が鳴るのは、スマホにも固有振動というものが存在しているからです。

そんな固有振動ですが、計算することで固有振動数を求めることができます。

計算で求めることができる固有振動の中で最も簡単なのが弦についてなので、今回は弦の固有振動についてわかりやすく簡単に解説をしていきます。

弦の固有振動とは

ギターやバイオリンのように、弦を弾くと一定の高さの音が出ます。この音が弦の固有振動となります。

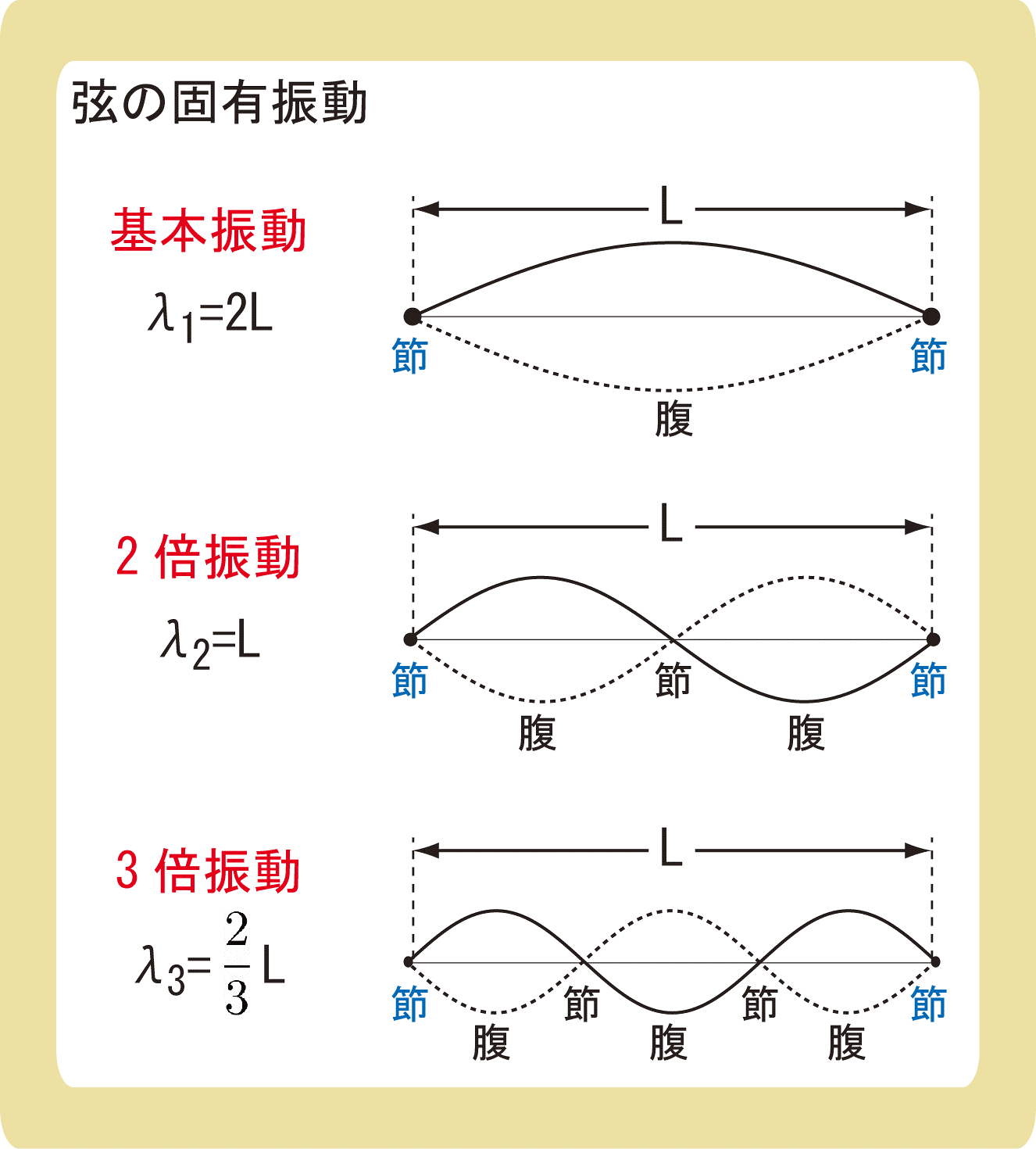
弦を振動させると、弦の両端で何度も反射をし、定常波が発生します。
このとき、弦の両端は固定端であるため、上図のような定常波ができます。

弦の固有振動のうち、腹の数が1つできるような振動のことを基本振動、腹が2つだと2倍振動、腹が3つだと3倍振動といいます。(4倍、5倍と続きます。)

弦の長さをL［m］とすると(LengthのL)、基本振動での波長は\(λ_1=2L\)、2倍振動では\(λ_2=L\)、3倍振動では\(λ_3=\frac{2}{3}L\)となります。

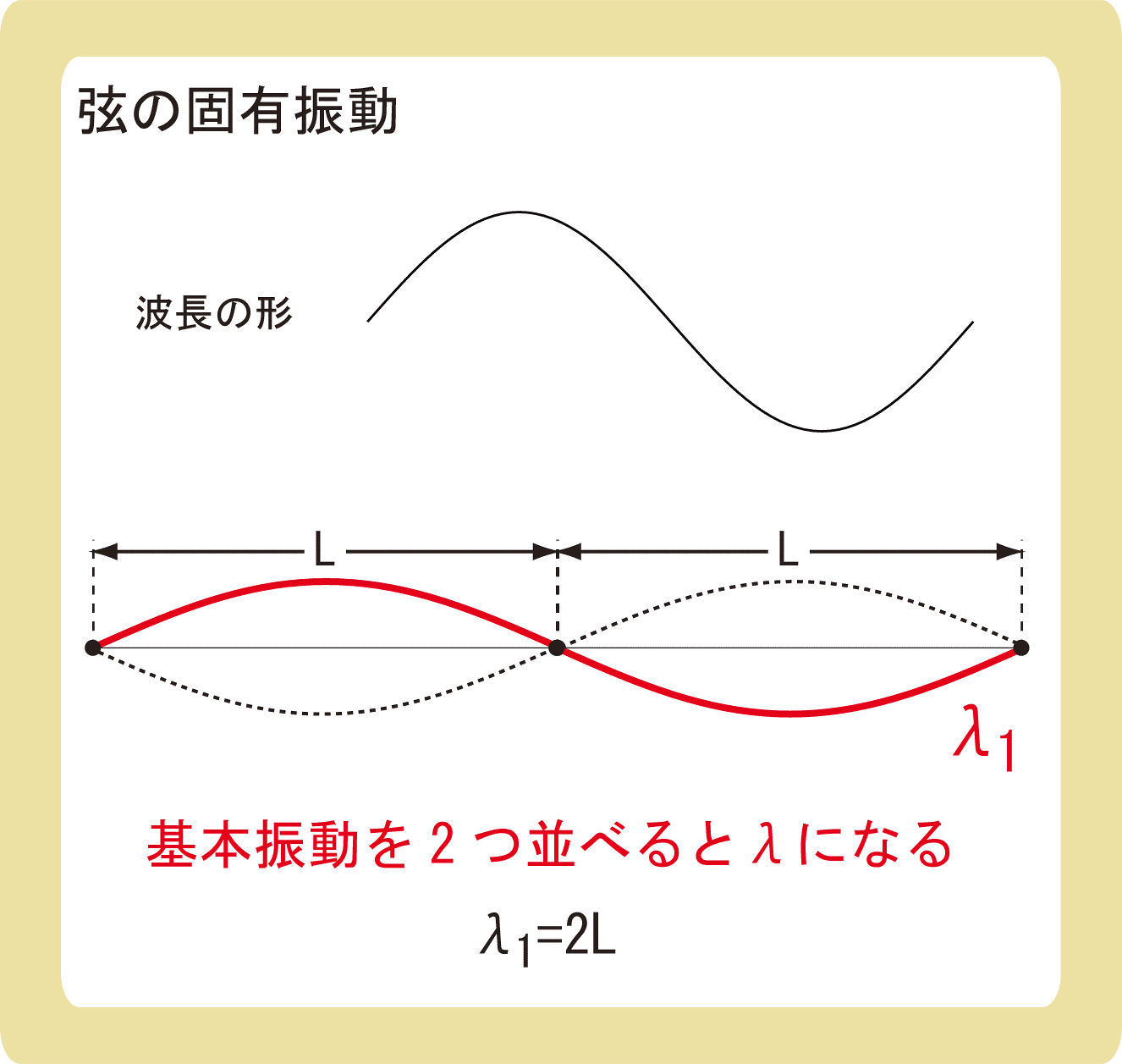
なぜ基本振動での波長が\(λ_1=2L\)になるのかは、図を見ると分かります。
波長λの形は、山と谷がくっついているような形として考えることができます。

基本振動は波長の半分しか入っていないため、基本振動の波を伸ばしてあげると、弦の長さLの2倍である2Lが波長の形になっていることが分かります。
つまり、\(λ_1=2L\)になるということです。

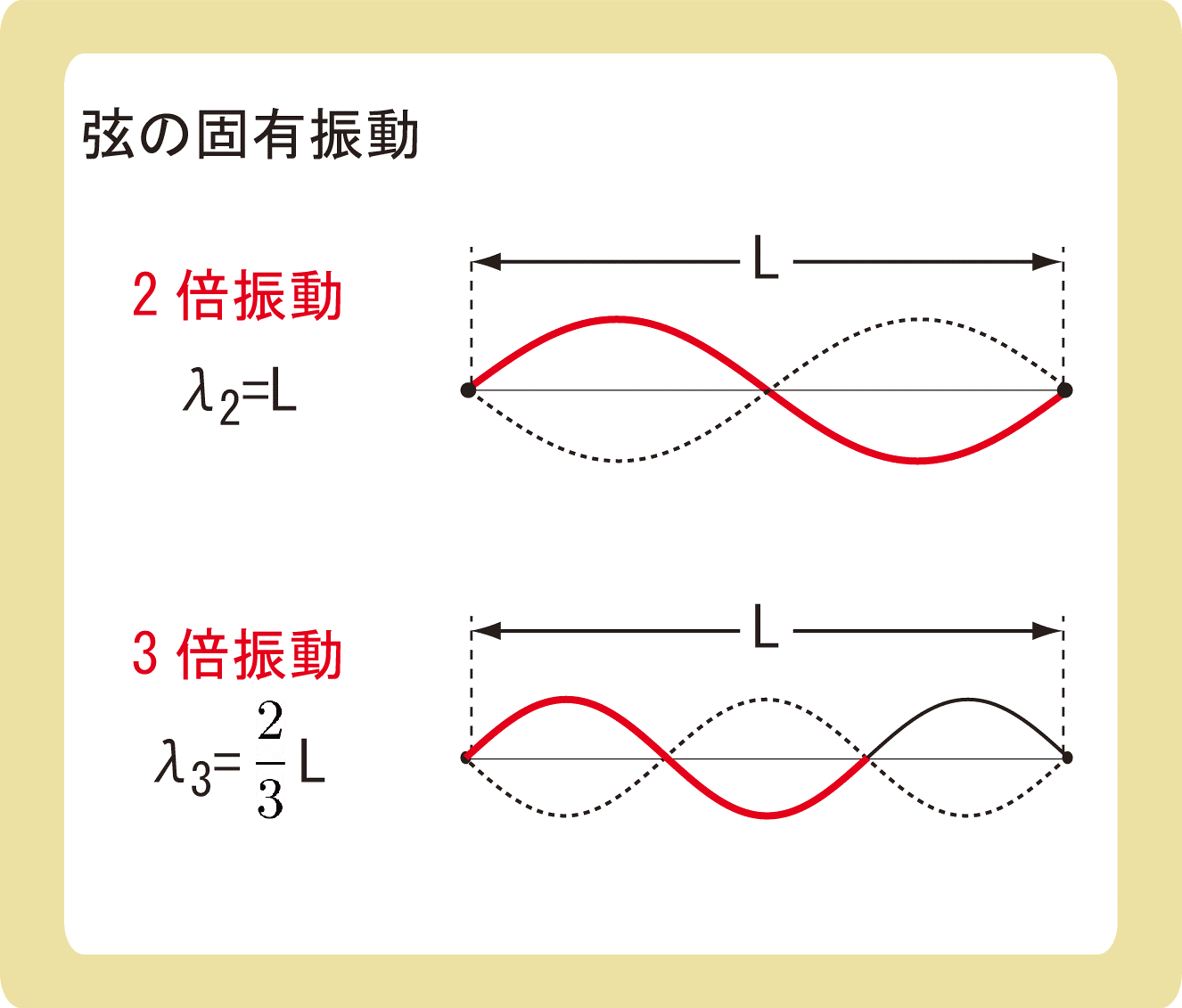
同様に、2倍振動と3倍振動でも、山と谷がくっついたようなλの形を探します。
上図の赤線の部分が波長λになるため、2倍振動では\(λ_2=L\)、3倍振動では\(λ_3=\frac{2}{3}L\)となります。

定常波の腹の数をmとすると、m倍振動での波長\(λ_m\)は

$$λ_m=\frac{2L}{m}$$

と表すことができます。(mは整数、m=1, 2, 3, ……)

正直、この公式を覚えていなくても、基本振動・2倍振動・3倍振動の形さえ覚えていれば、λの値を図から読み取ることができるはずです。
頑張って式を1つ暗記するくらいなら、基本振動・2倍振動・3倍振動の形を覚えた方が簡単であると思います。

また、\(v=fλ\)より、

$$v=f_mλ_m\\
v=f_m×\frac{2L}{m}\\
f_m=\frac{mv}{2L}$$

という式もあるのですが、この式を暗記するくらいなら他のことを覚えた方がよいでしょう。なぜなら、\(v=fλ\)で簡単に求めることができるのですから。

弦を伝わる波の速さ

弦を伝わる波の速さは

$$v=\sqrt{\frac{S}{ρ}}$$

で表されます。
Sは張力［N］、ρ(ロー)は線密度［kg/m］です。

力学をしっかり勉強した人は、「張力はTじゃないの？」と思うかもしれませんが、Tは周期Tとして使ってしまっているので、仕方なくSを使っています。
また、浮力にも登場したρは、密度［kg/m³］ではなく、線密度［kg/m］として使います。弦1mあたりの質量という意味ですね。

ギターやベースを触ると分かるのですが、弦を強く張ると音は高くなり、弦が太くなると音は低くなります。

\(v=fλ\)を考えましょう。
弦の長さが変わらない場合、λの大きさは変わりません。(同じλじゃないと大きく振動しません。)
音が高くなるということは振動数fが大きくなるということです。

fが大きくなりλが一定なままということは、\(v=fλ\)を考えると速さvは大きくなるといえます。

逆に、音が低くなる＝fが小さくなるということは、速さvは小さくなるということです。

$$v=\sqrt{\frac{S}{ρ}}$$

この式は、弦を強く張ると波が速くなる＝音が高くなる、弦が太くなると(線密度が大きいと)波が遅くなる＝音が低くなる、ということを表しています。

なお、問題によっては「弦を伝わる波の速さは、張力の大きさの平方根に比例し、線密度の平方根に反比例する」と書いてある場合もあります。

例題

例題1

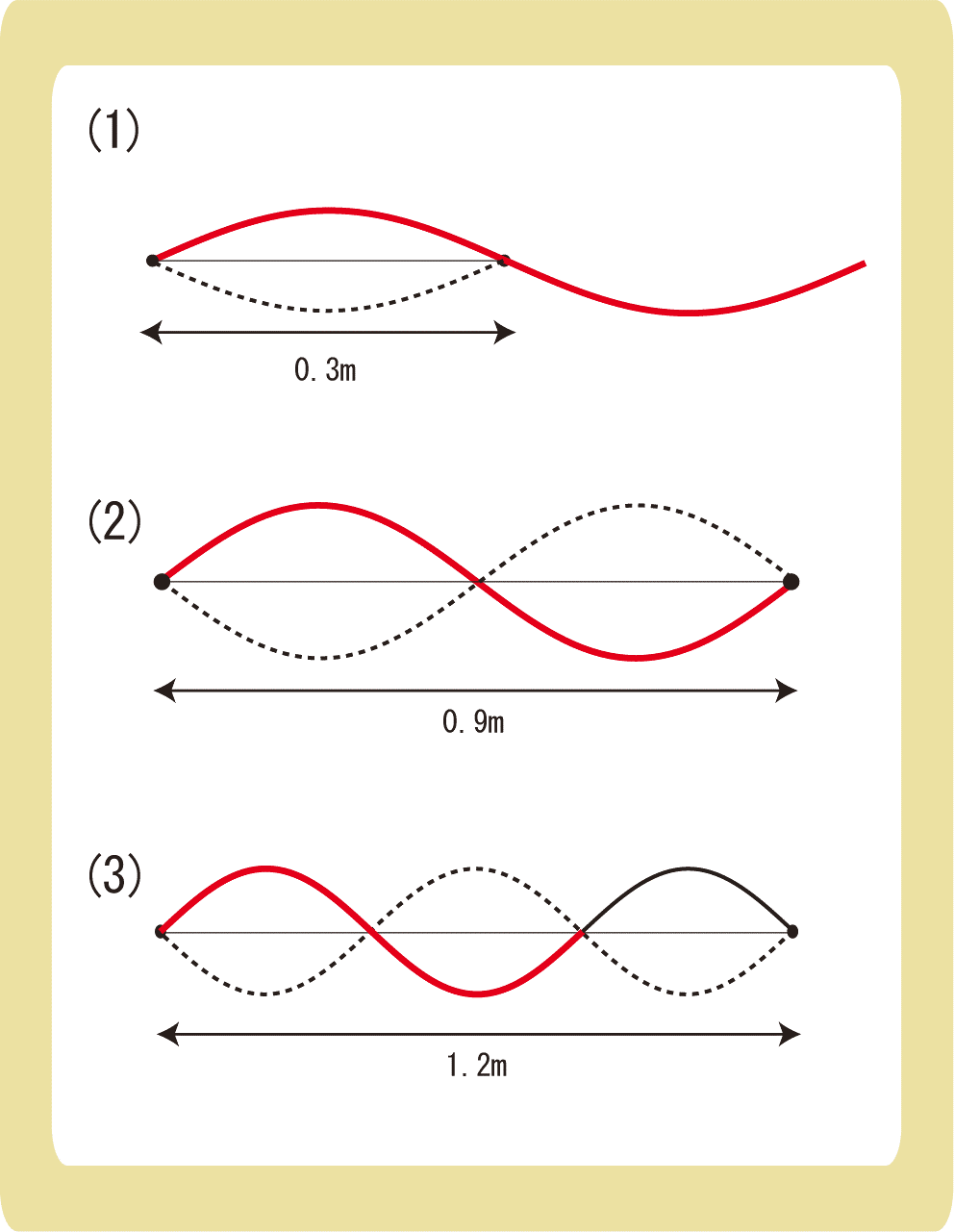
下図のように、両端を固定した弦を下図のように振動させた。弦を伝わる波の波長は何ｍか。

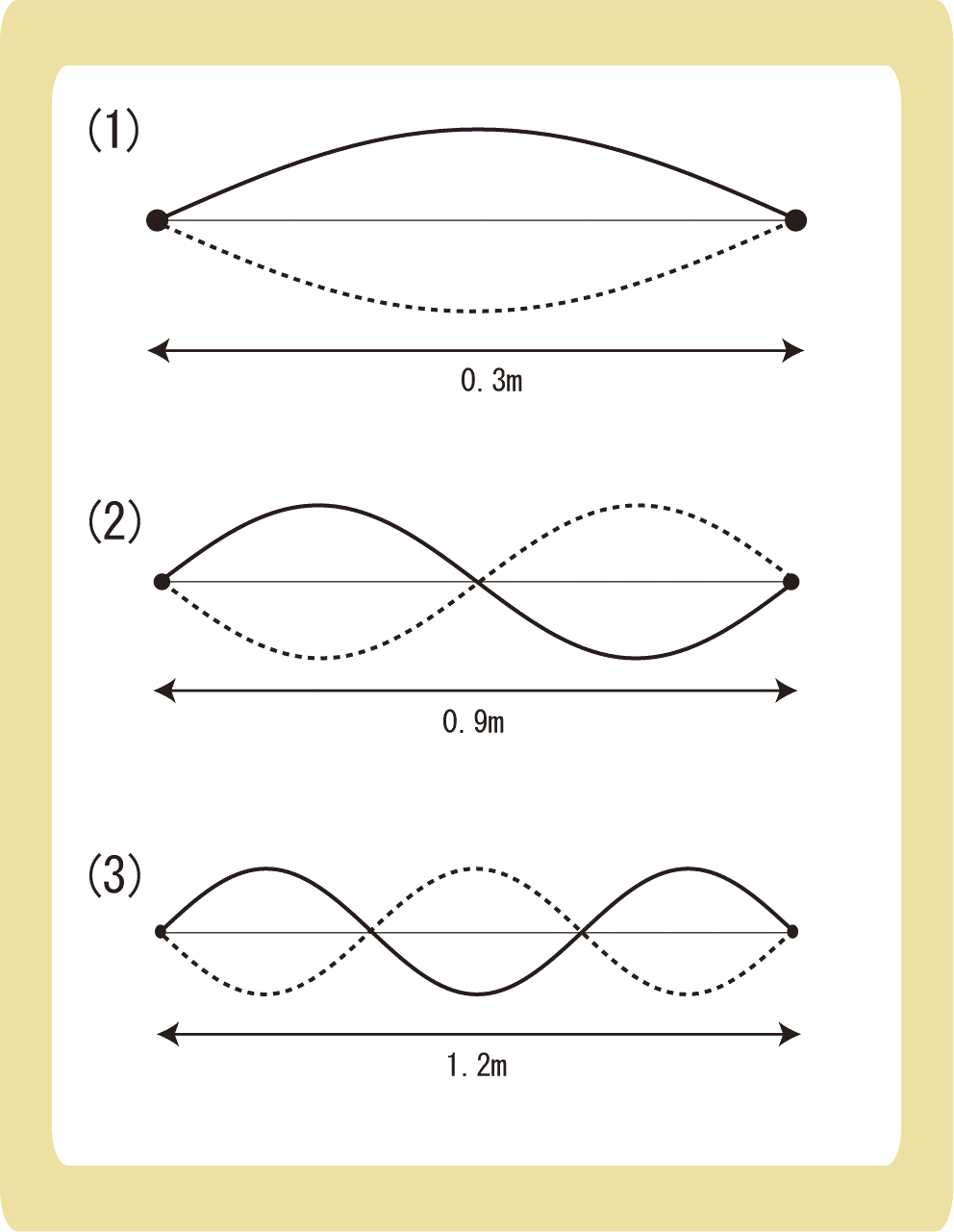
例題2

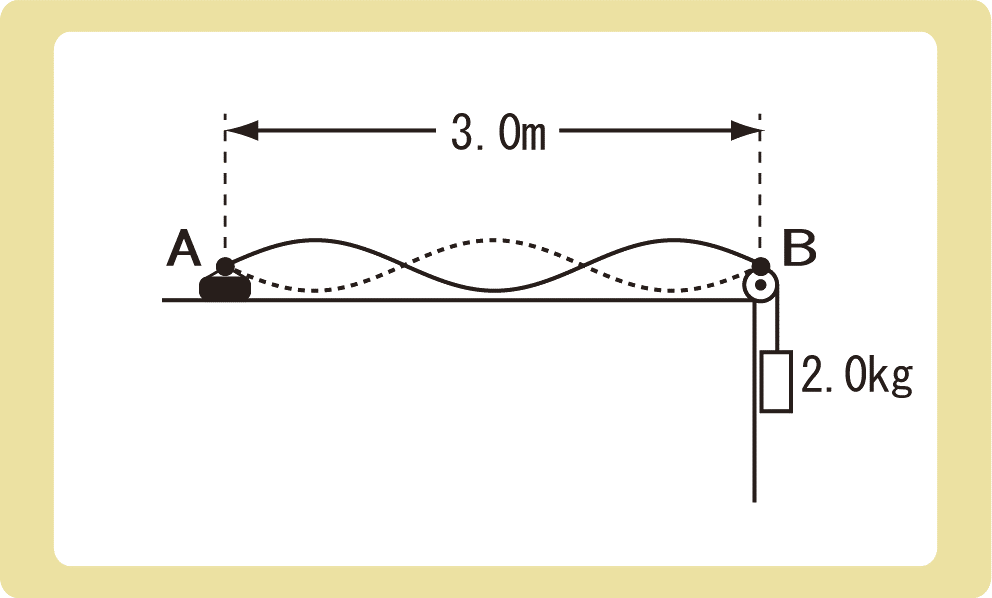
下図のように、弦の一端にスピーカーを取り付け、滑車を通して質量2.0kgのおもりをつるした。スピーカーの振動数が10Hz、ABの長さが3.0mのとき、弦に腹が3つの定常波ができた。以下の問に答えなさい。ただし、重力加速度の大きさを9.8m/s²とする。
(1)弦を伝わる波の波長を求めなさい。
(2)弦を伝わる波の速さを求めなさい。
(3)この弦の線密度を求めなさい。

まとめ

弦を弾くと一定の高さの音が鳴ります。
一定の高さの音が鳴るということは、その音が弦の固有振動ということですね。

弦の固有振動には、定常波の腹の数に応じて、基本振動・2倍振動・3倍振動と名前がついています。
それぞれの振動における波長は

$$λ_m=\frac{2L}{m}$$

という式で表されるのですが、図から波長を読み取った方が良いでしょう。

また、弦を伝わる波の速さは

$$v=\sqrt{\frac{S}{ρ}}$$

という式で表されます。余裕がある場合は、この式は覚えておきましょう。

 

次の内容はこちら

一覧に戻る