・気柱の共鳴とは
・閉管と開管とは
・開口端補正とは
物理基礎の波動の範囲も今回で最後です。
今回は，フルートやトランペットなどの管楽器の音の仕組みに関係する気柱の共鳴について，わかりやすく簡単に解説をしていきます。
気柱の共鳴とは
貝殻を耳に当てると海の音が聞こえる，なんてことを聞いたことはありますか？
貝殻だけでなく，お茶碗やトイレットペーパーの芯を耳に当てても，「ゴーッ」という音が聞こえてきます。
実は，この音は海の音ではなく，貝殻やお茶碗の中にある空気の柱(気柱)が，外のノイズと共鳴して大きくなった音なのです。
管の中の空気の長さによって，どんな音が鳴るのか決まるため，気柱は固有振動を持っていると考えることができます。
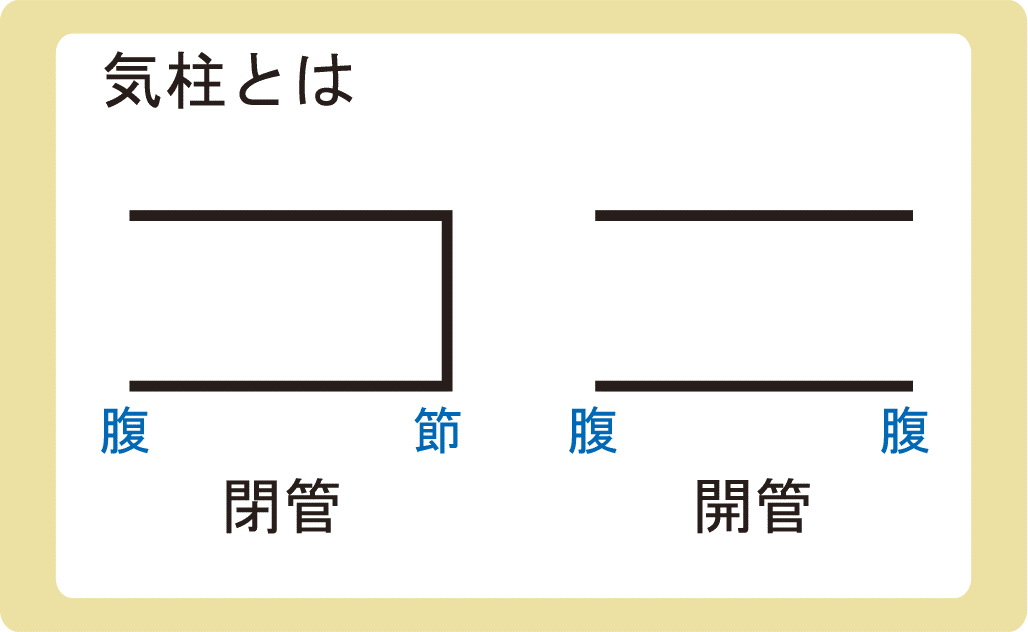
気柱の中でも，コップのように片方が閉じている管のことを閉管，トイレットペーパーの芯のように両端が開いている管のことを開管といい，別々に考えます。
閉管とは
管の片方が閉じている管
閉じている端は節，開いている端は腹となる
$$λ_m=\frac{4L}{2m-1}$$
(L：弦の長さ［m］
m=1, 2, 3, ……)
閉管とは，管の片方が閉じている管のことをいいます。
管の中に定常波ができるとき，閉じている端は節に，開いている端は腹になります。
気柱を振動させると，管の両端で何度も反射をし，定常波が発生します。
このとき，上図のように，管の底では節，開口端では腹になるように定常波ができます。
閉管では，節の数が1つできるような振動のことを基本振動，節が3つだと3倍振動，節が5つだと5倍振動といいます。(7倍，9倍と続きます。)
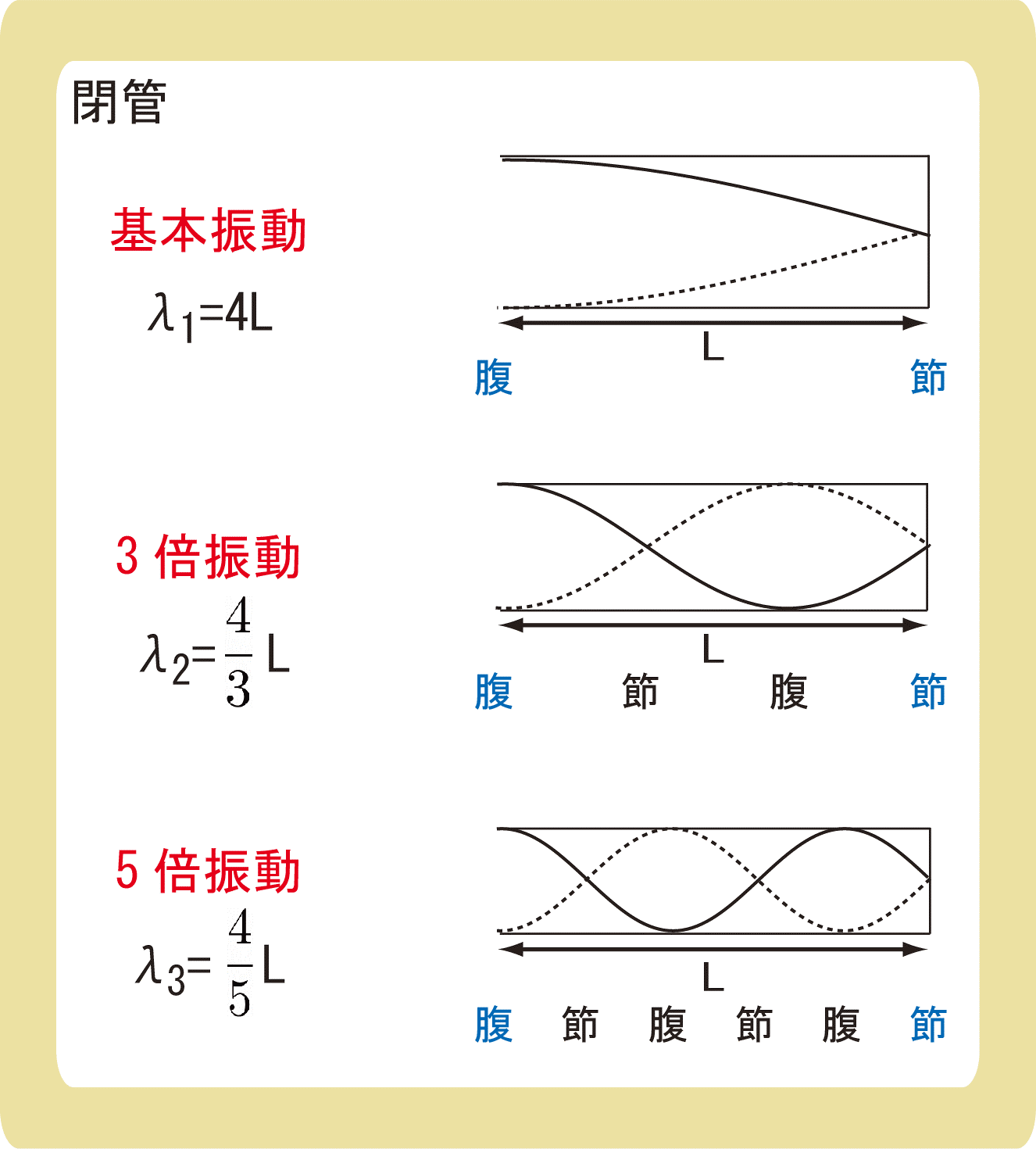
管の長さをL［m］とすると，基本振動での波長は\(λ_1=4L\)，3倍振動では\(λ_2=\frac{4}{3}L\)，5倍振動では\(λ_3=\frac{4}{5}L\)となります。
基本振動・3倍振動・5倍振動と，奇数倍の振動しか存在しないため，λ2は3倍振動，λ3は5倍振動なのがややこしいですが，そればかりは仕方ありませんね。
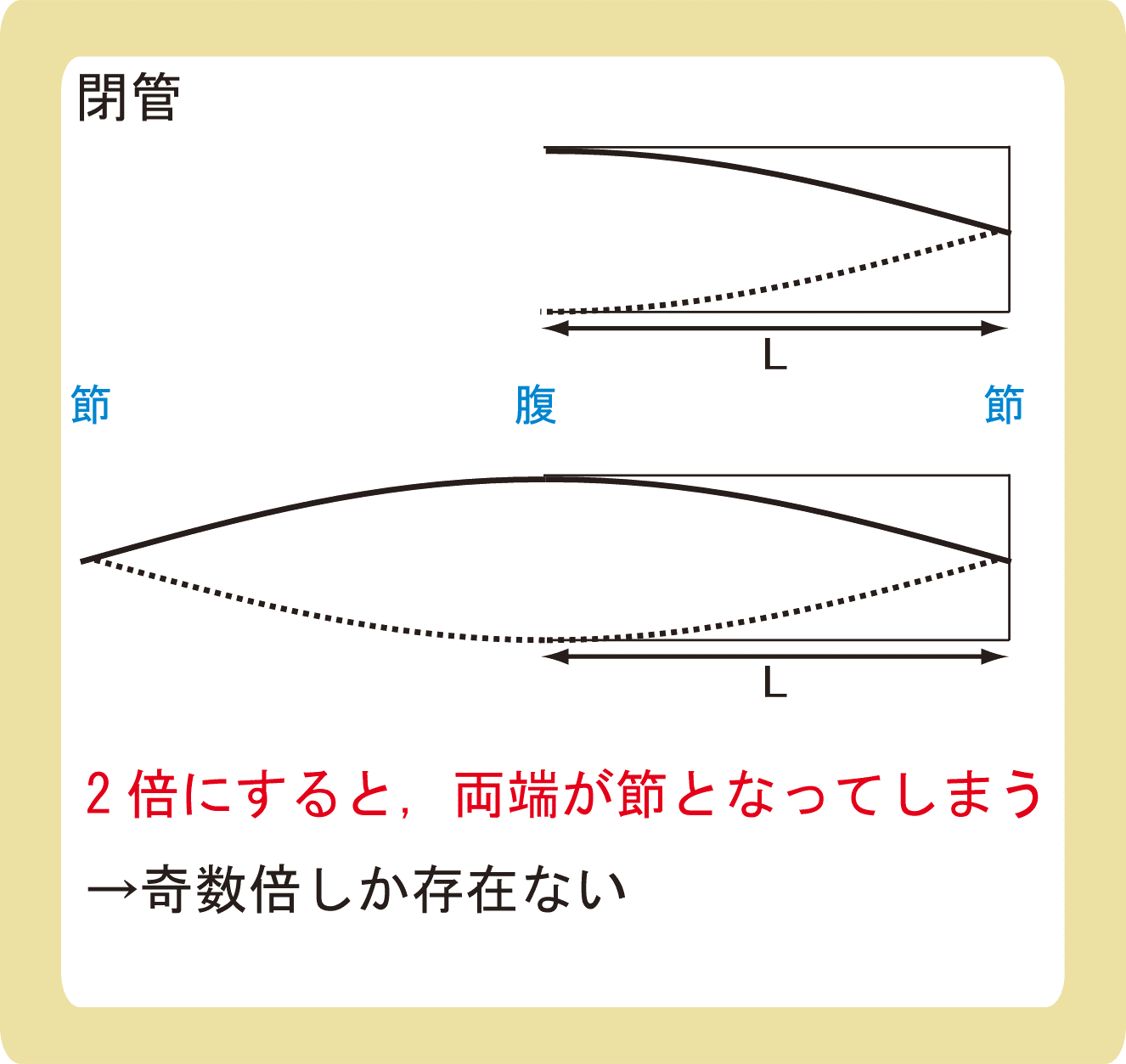
閉管では，2倍振動や4倍振動などの偶数倍では大きく振動しません。
もし2倍振動があったとすると，2倍振動では両端が節となるような振動になってしまうため，閉管では共鳴しないのです。
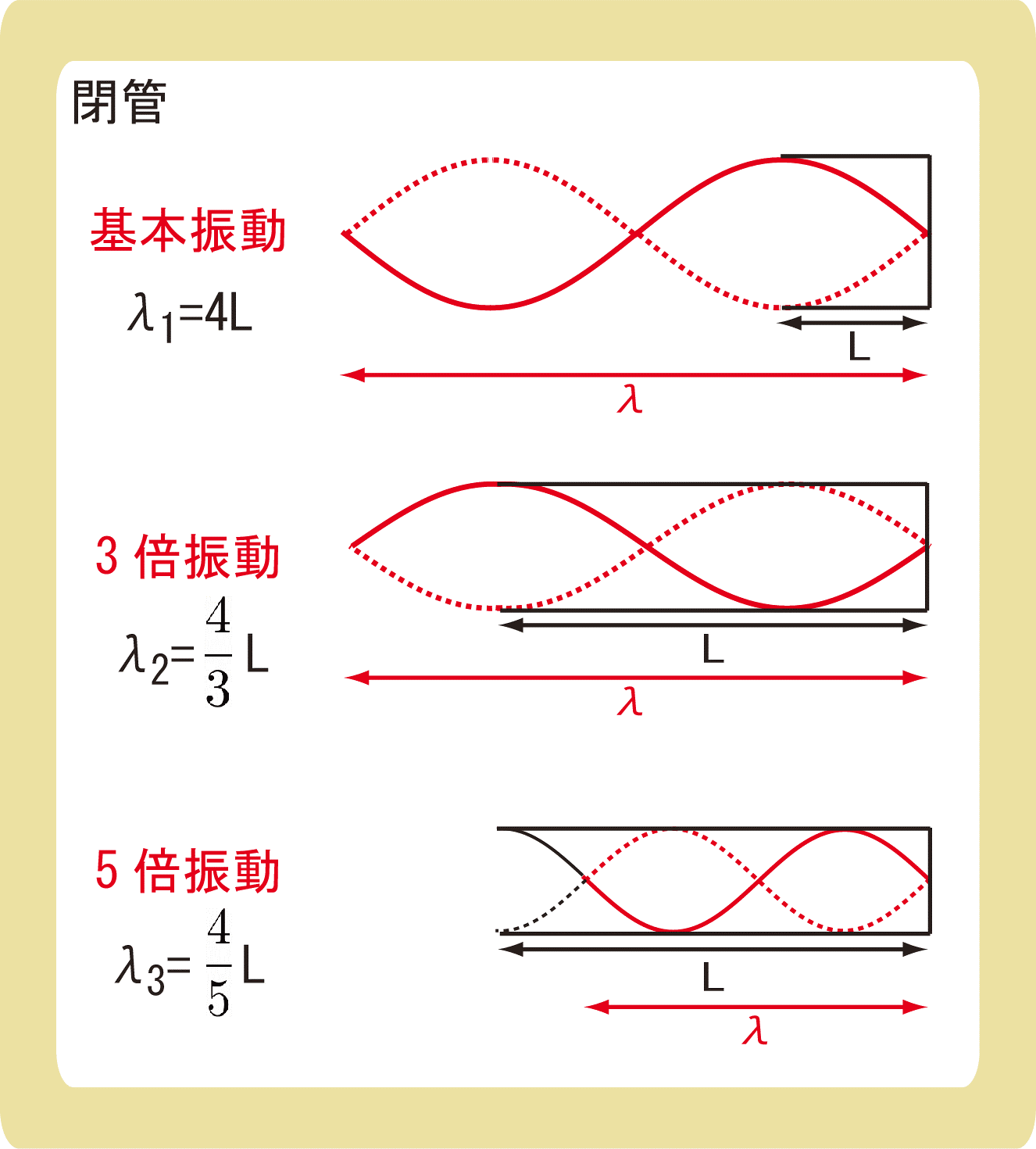
基本振動での波長は\(λ_1=4L\)，3倍振動では\(λ_2=\frac{4}{3}L\)，5倍振動では\(λ_3=\frac{4}{5}L\)になる理由は上図の通りです。
基本振動では，管の中に波長の\(\frac{1}{4}\)しか入っていないため，管の長さLの4倍がλになります。
同様に，3倍振動では，管の中に波長の\(\frac{3}{4}\)しか入っていないため，管の長さLの\(\frac{4}{3}\)倍がλになり，
5倍振動では，管の長さLの\(\frac{4}{5}\)倍が波長となります。
これらをまとめて
$$λ_m=\frac{4L}{2m-1}$$
と表すこともありますが，図からλが分かるのであれば，わざわざ覚えなくても大丈夫です。
開管とは
両端が開いている管
両端が腹となるように定常波ができる
$$λ_m=\frac{2L}{m}$$
(L：弦の長さ［m］
m=1, 2, 3, ……)
開管とは，両端が開いている管のことをいいます。
管の中に定常波ができるとき，どちらも開いているため，両端が腹になります。
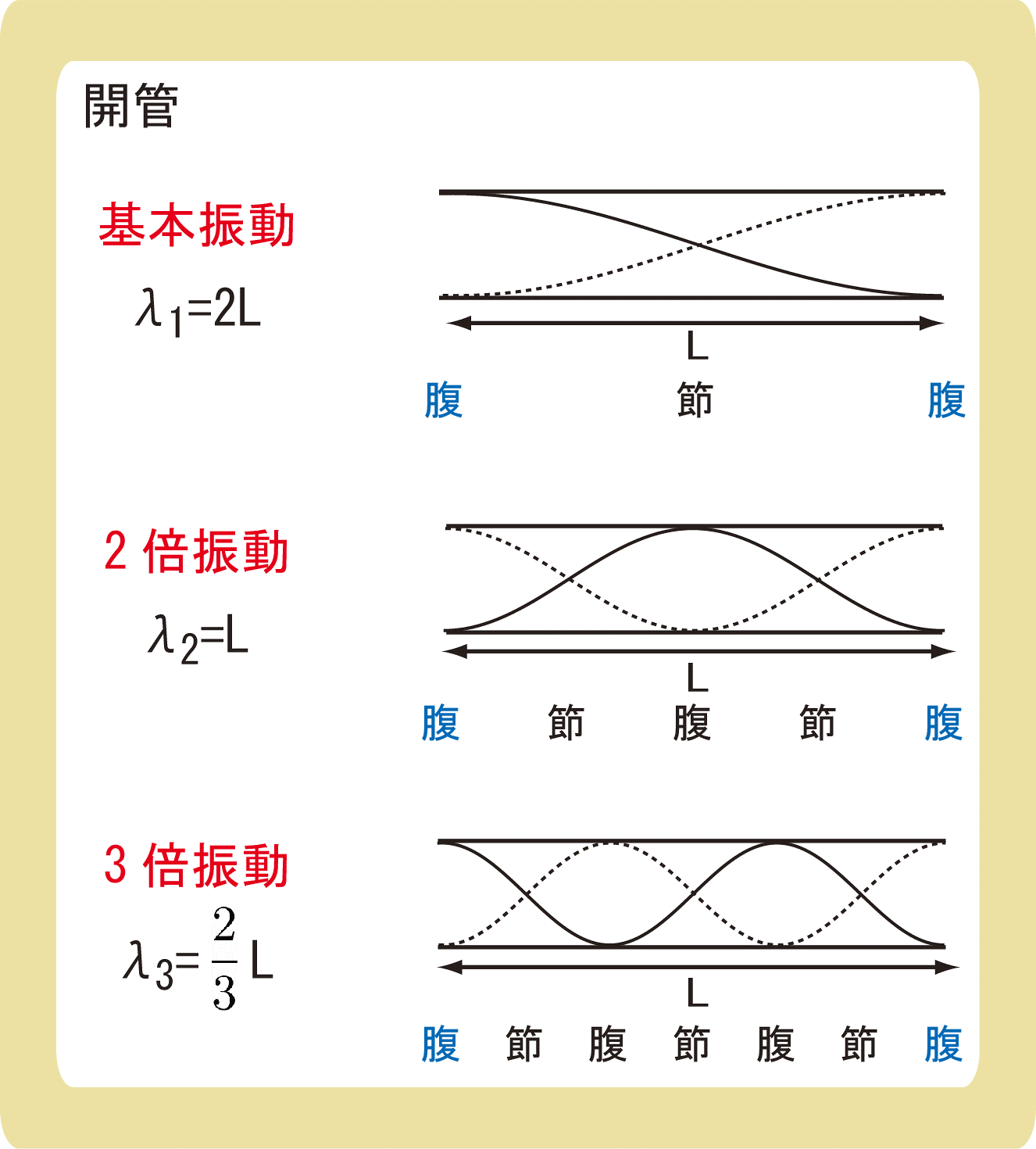
開管では，両端が腹になるような定常波ができます。
偶数倍の振動もあるので，閉管よりも分かりやすいですね。
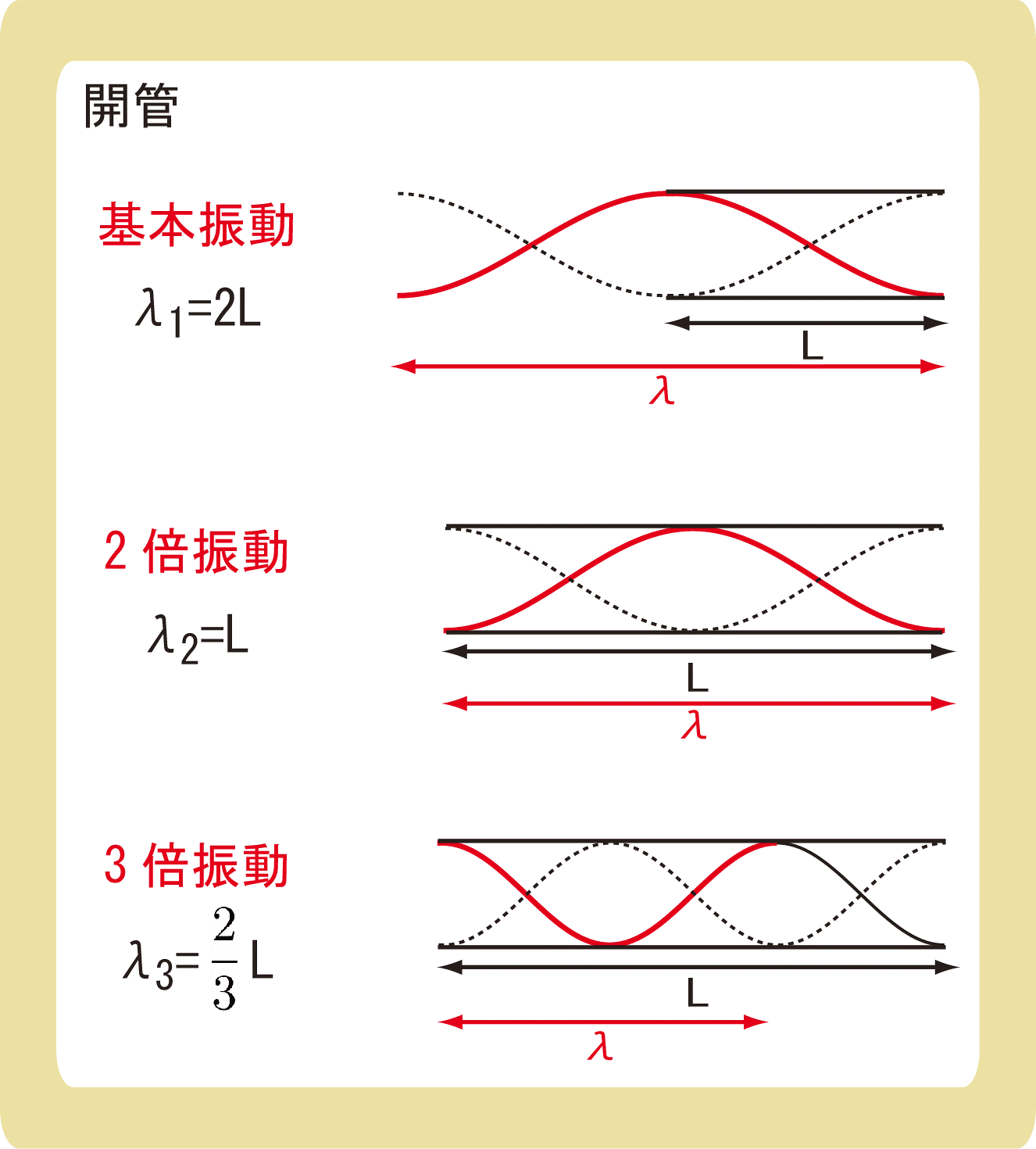
それぞれの波長λの大きさがどれくらいなのかは，上図を参照してください。
波長は山から山・谷から谷の長さでもあるので，図の赤で描いた波が波長になります。
基本振動での波長は\(λ_1=2L\)，2倍振動では\(λ_2=L\)，3倍振動では\(λ_3=\frac{2}{3}L\)となります。弦の固有振動の波長と同じですね。
開口端補正とは
開口端では定常波の腹が少しはみ出てしまいます。
開口端補正とは，定常波の腹が管口からはみ出た長さのことをいいます。
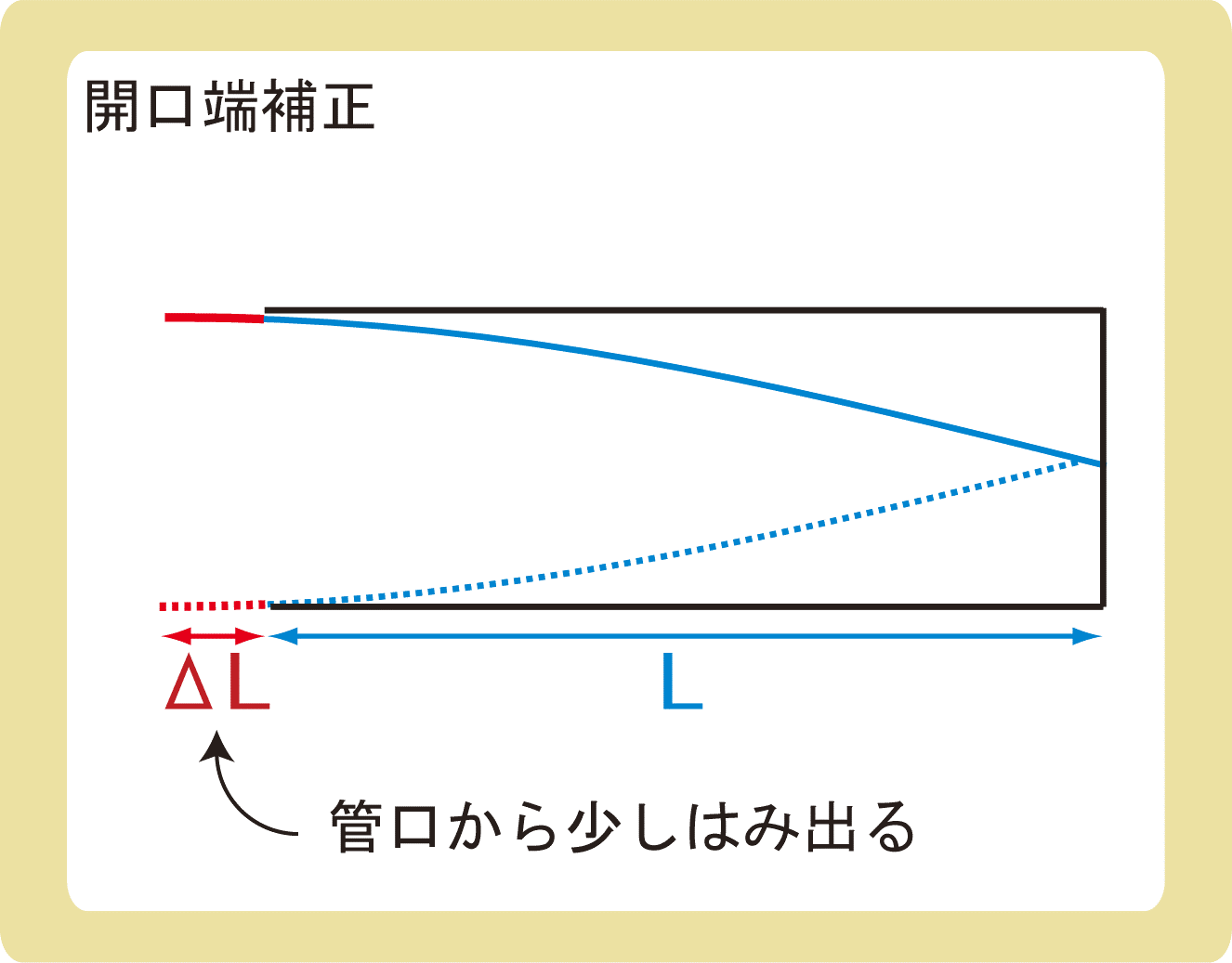
開口端補正を無視するか無視しないかは，問題文に必ず書いてあります。
「開口端補正を無視する」「定常波の腹を開口端の位置とする」のようなことが書いてあった場合は，開口端補正を無視しましょう。
例題
例題1
閉管に音を出し，下図のように振動させた。このとき，音の波長はそれぞれ何ｍか答えなさい。ただし，開口端を腹の位置とする。
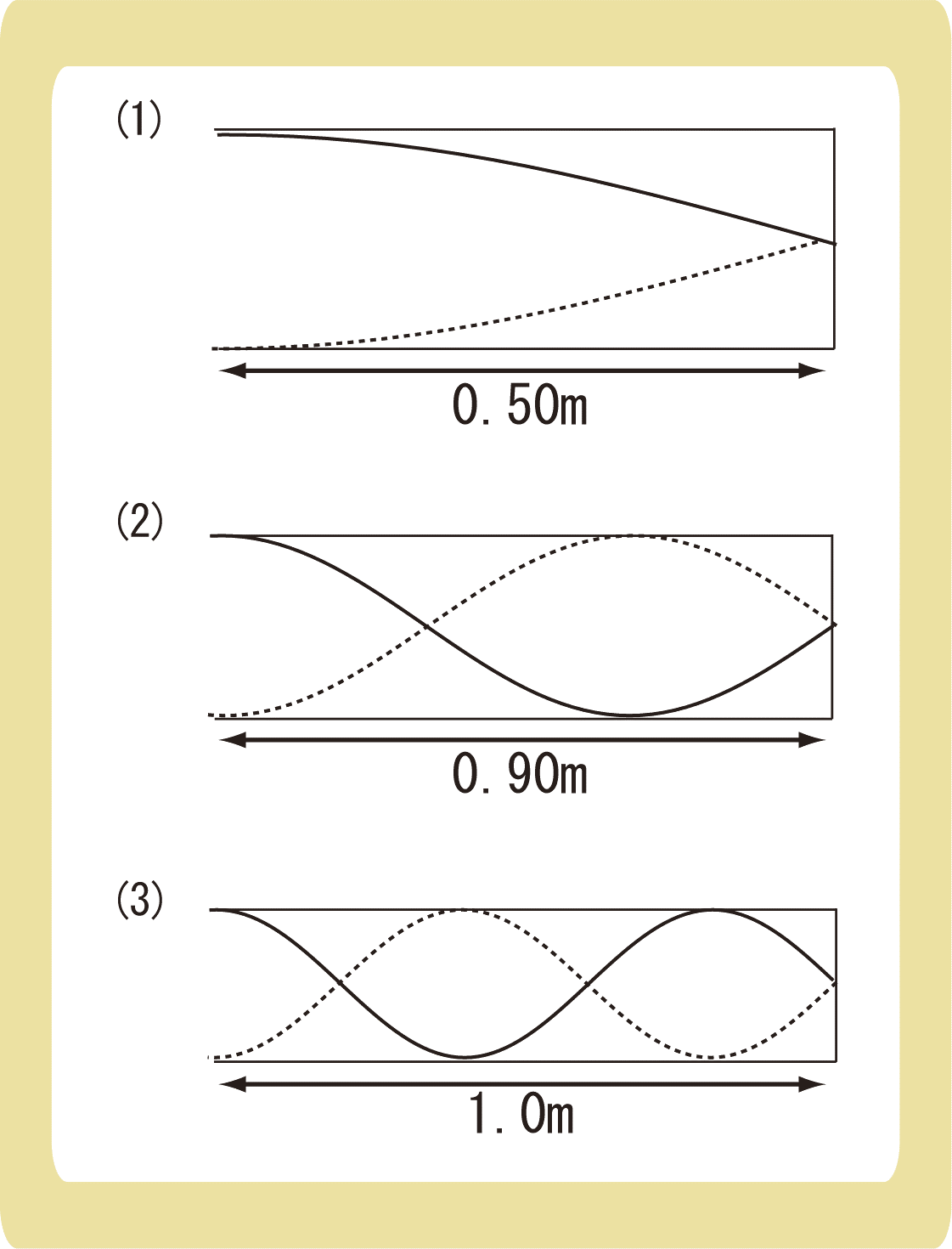
例題2
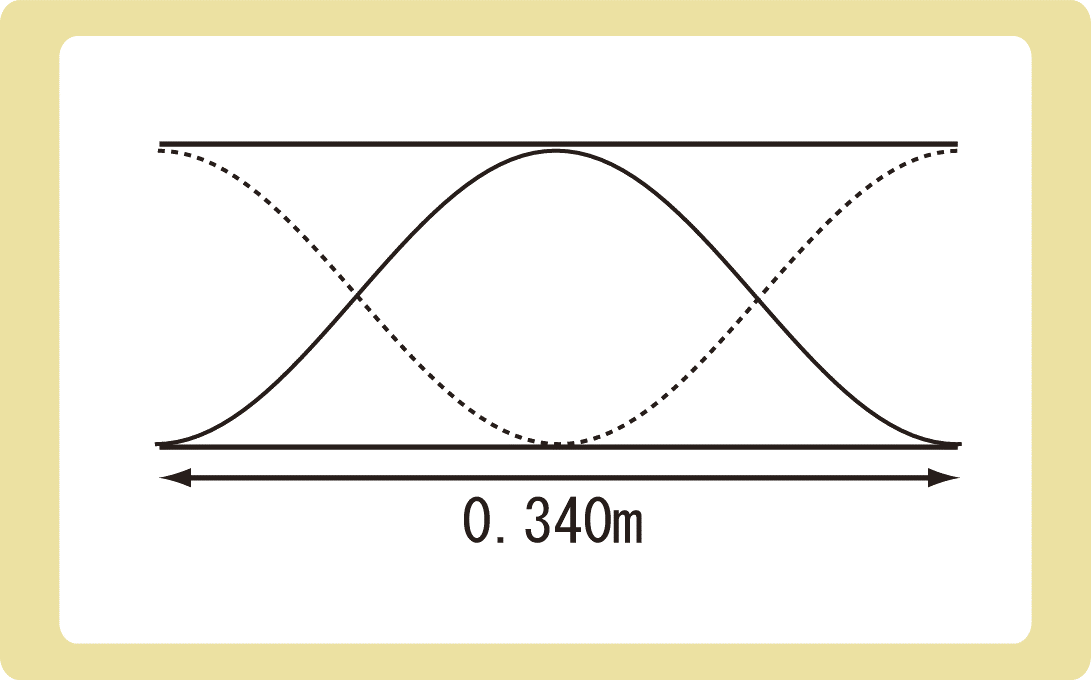
長さが0.340mの開管の管口付近におんさを近づけ管を共鳴させると，下図のような定常波が生じた。以下の問に答えなさい。ただし，音速を340m/sとし，開口端補正は無視できるものとする。
(1)この音波の波長は何mか。
(2)この音波の振動数は何Hzか。
(3)同じ長さの管に3倍振動を起こすためには何Hzの振動数が必要か。
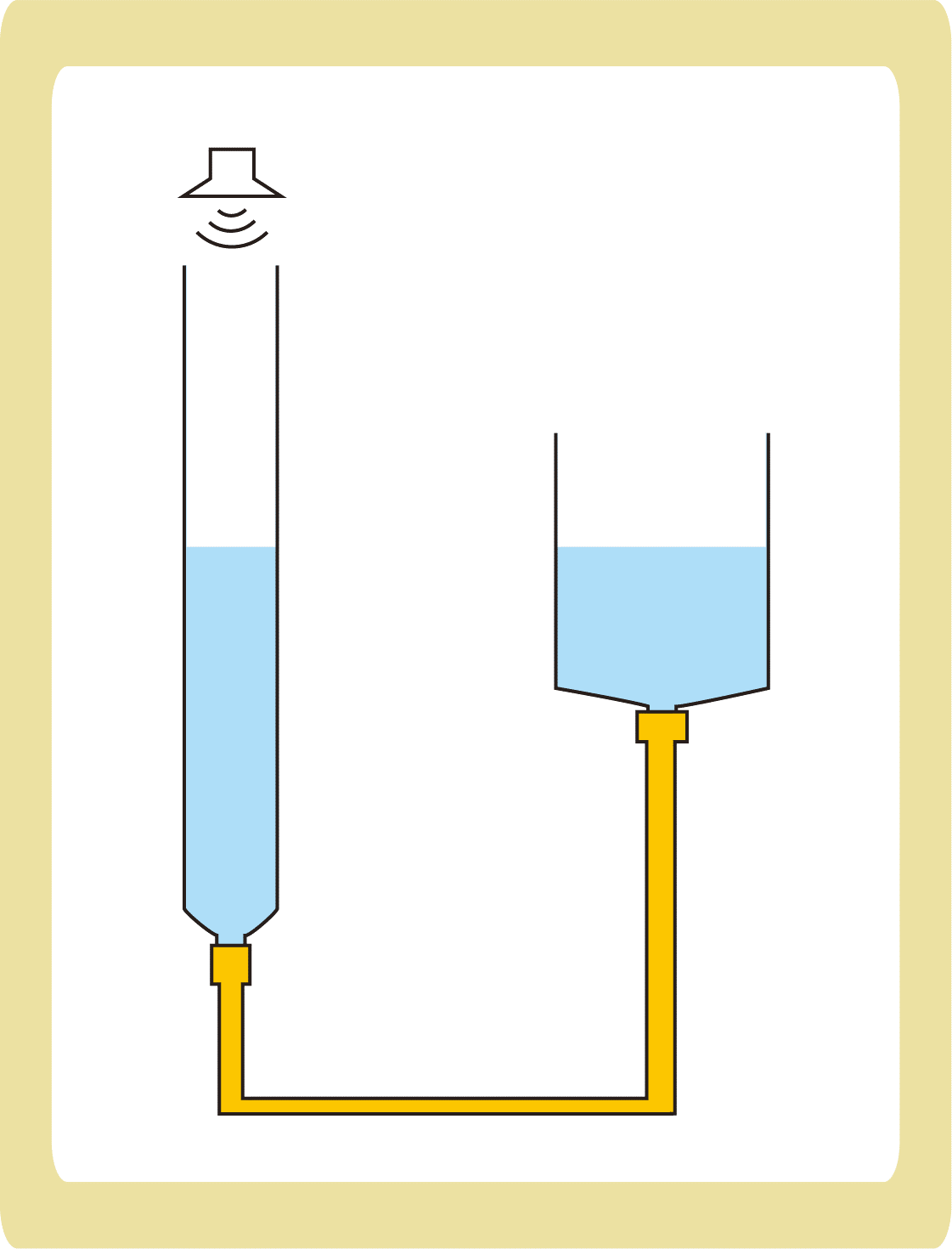
例題3
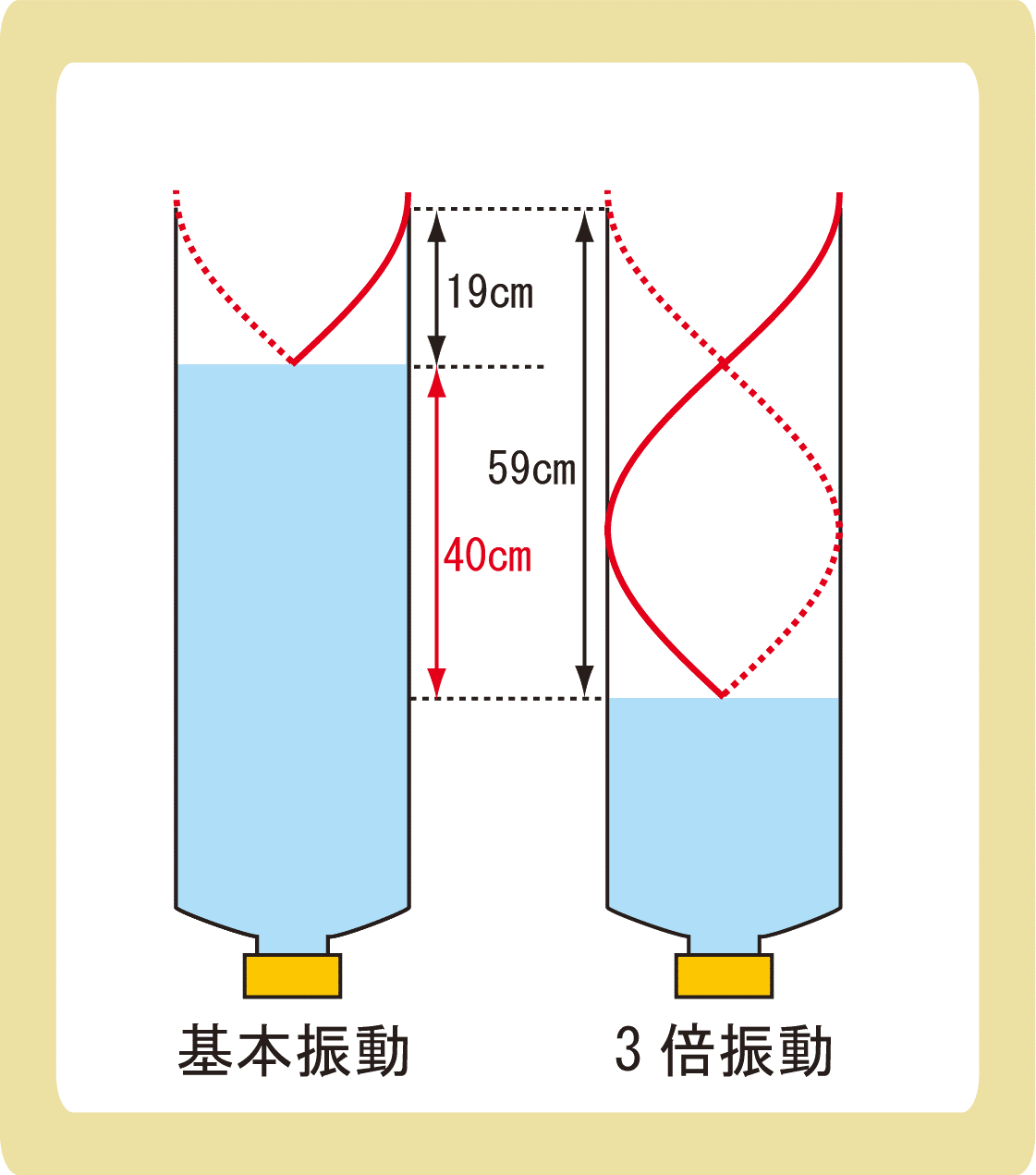
下図のような気柱共鳴装置を用いて実験を行った結果，水面が管口から19cmと59cmのところで音が大きくなった。次の各問に答えなさい。ただし，音速を340m/sとする。
(1)音波の波長は何mか。
(2)音波の振動数は何Hzか。
(3)閉口端補正は何cmか。
気柱の共鳴実験とは，水面を上下させ管の長さを変化させ，音が大きくなる(共鳴した)ときの管の長さを測る実験です。
図の右側にある器具を上下に動かすことにより，左側にある管の水面を調節することができます。
水面は固定端となるため，閉管の共鳴となっています。
また，(3)でも聞かれていますが，今回は開口端補正があることに気を付きましょう。
(1)
21cmと61cmで共鳴したときの様子はこの図のようになります。
閉管には2倍振動がないため，2回目の共鳴での水面の位置は，1回目の共鳴での水面の位置の約3倍の長さになっています。
閉管なので基本振動の波長\(λ_1=4L\)や3倍振動\(λ_2=\frac{4}{3}L\)を使いたいところですが，今回はこの式を使ってはいけません。
基本振動では管の長さが19cmですが，開口端補正のせいで定常波の腹がはみ出ている状態なので\(λ_1=4L\)が使えないのです。
じゃあどうするのかというと，図から波長を見つけるしかありません。
上図のように，基本振動と3倍振動での水面の位置の差を考えます。
2つの差である40cmの部分は，管からはみ出ていないため，ちょうど波長の半分であると考えることができます。
つまり，
$$\frac{λ}{2}=0.40\\
λ=0.80$$
∴0.80m
なお，cmはmに直して計算をします。
(2)λが分かれば\(v=fλ\)を使います。
$$ v=fλ\\
340=f×0.80\\
f=425$$
∴425Hz
(3) (1)より，波長は80cmであることが分かりました。
開口端補正が無ければ，基本振動の管の長さは波長の\(\frac{1}{4}\)倍であるはずなので，今回なら20cmのはずです。
しかし，開口端補正のせいで，1回目の共鳴は19cmの位置となっており，これは20cmのうち1cmがはみ出たことといえますよね。従って，開口端補正は1cmとなります。
∴1cm
まとめ
気柱の共鳴には，片方が閉じている閉管と両端が開いている開管というものがあります。
どちらの管も，図から波長を見つけられるかどうかが大事になっています。
また，定常波の腹が管からはみ出る開口端補正というものを考えるときもあります。その場合，はみ出ていないところの波の様子から波長を見つけましょう。
