モンティホール問題は、「答えを教えてもらってもどうしても納得ができない!」ことで超有名な数学の問題です。
モンティ・ホールが司会を務めるアメリカのテレビ番組『Let’s make a deal』で出題された問題で、「答えが納得できない!」と数多くの反響があったようです。
私も子供の頃、この問題を理解するのにかなり時間がかかりました。
今回は、モンティホール問題とは何かについて、分かりやすく簡単に解説していこうと思います。
モンティホール問題とは
まずはモンティホール問題を見てみましょう。




プレーヤーの前に閉じた3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。
ここでプレーヤーはドアを変更すべきだろうか?
以上がモンティホール問題です。
※注意
・司会者は正解のドアを知っている
・司会者は必ずはずれのドアを開ける
・正解の位置が変わることはない(司会者がはずれのドアを選んだ後、正解の位置がランダムに変更されることはない)
よくある誤答
モンティホール問題では、多くの人が以下のように考えてしまいます。

答えは①!
だって、残りのドアは2つなんだから、どっちのドアを選んでも当たる確率は\(\frac{1}{2}\)だよね?



答えは①!
そもそも正解する確率は\(\frac{1}{3}\)だから!
答えを知ってもどうしても納得できない人が多いようです。
モンティホール問題の正解と解説
モンティホール問題の正解と解説
正解は、「②残ったもう一つのドアを選んだ方が高くなる」です。
なんと、同じドアを選んだままにするよりも、残ったもう一つのドアを開ける方が車の当たる確率は2倍になります。



上の図で書いた通りなのですが、
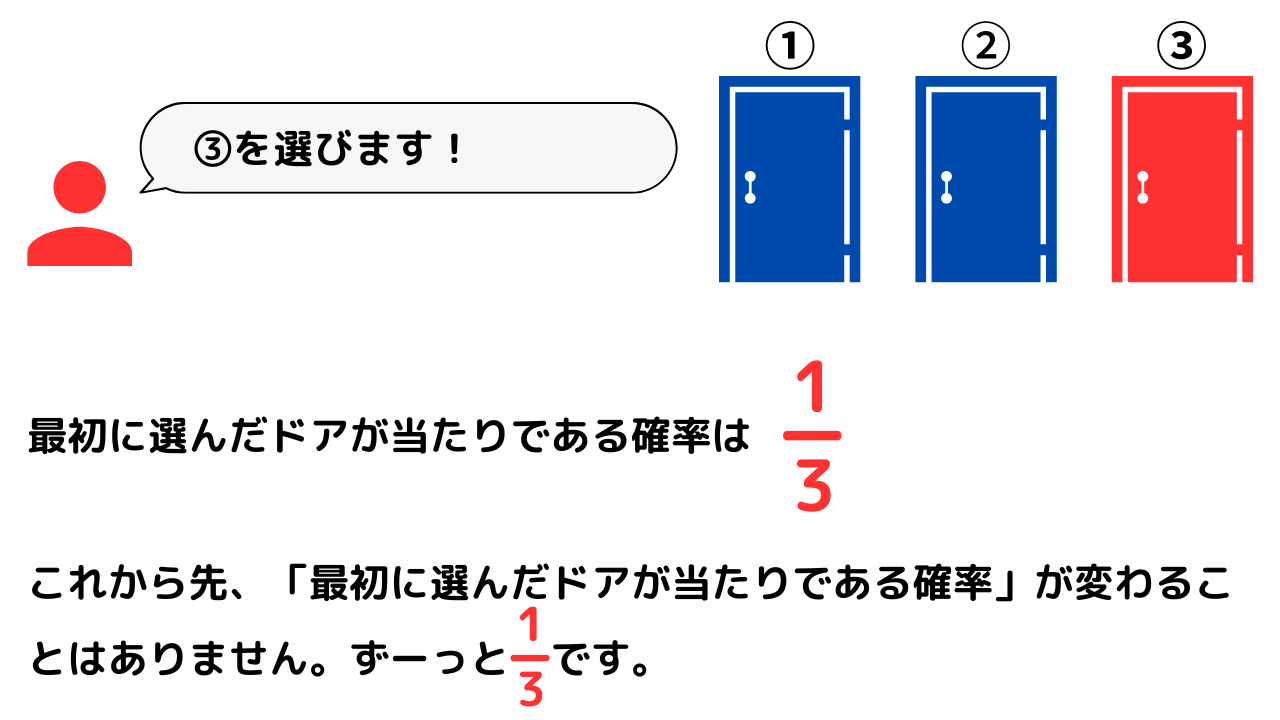
まず、最初に選んだドアが当たりである確率は\(\frac{1}{3}\)です。
これから司会者がはずれのドアを開けるのですが、司会者がはずれのドアを開けようが開けまいが、最初に選んだドアが当たりである確率は\(\frac{1}{3}\)から変わることはありません。
司会者がはずれのドアを開け、残りのドアが2つになってからもう一度最初に選んだドアを選び直したとしても、最初に選んだドアが当たりである確率は\(\frac{1}{3}\)です。
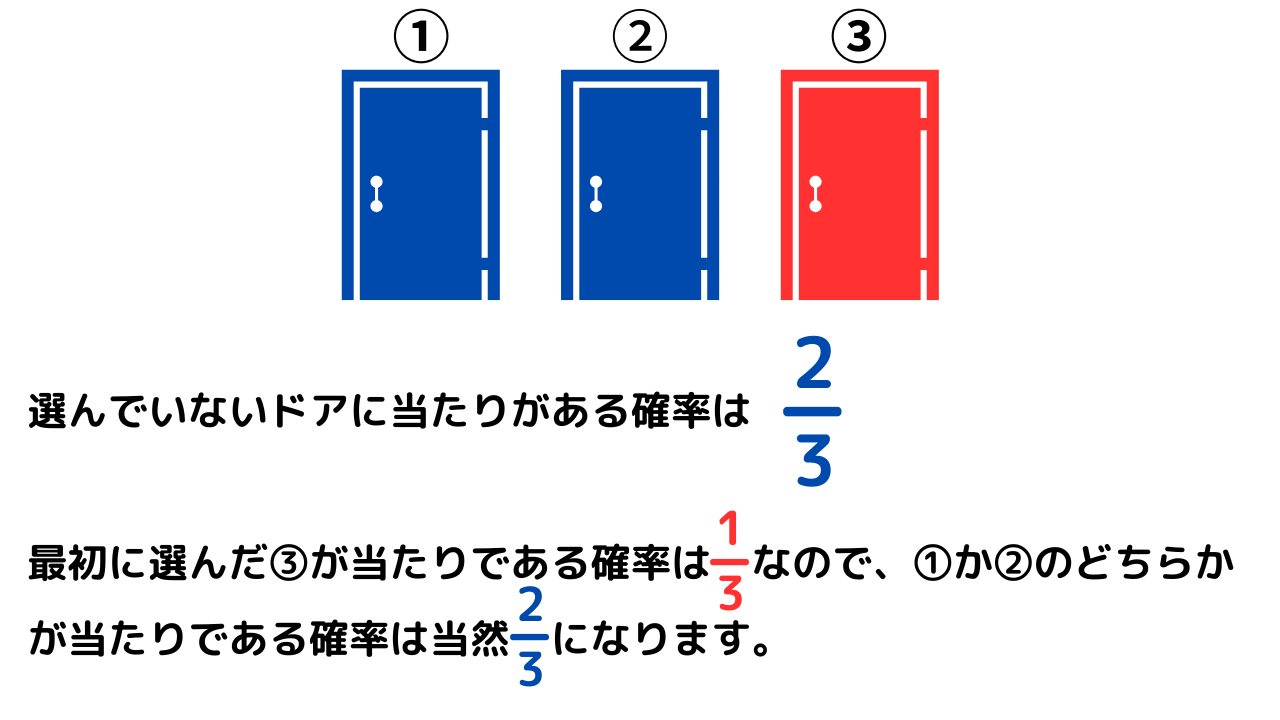
次に、最初に選ばなかった2つのドアが当たりである確率はそれぞれ\(\frac{1}{3}\)なので、2つ合わせると\(\frac{2}{3}\)です。
言い換えると、最初に選んでいないドアが当たりである確率は\(\frac{2}{3}\)と言えます。
ここまでは大丈夫ですよね。
ここで、司会者がはずれのドアを一つ開けます。
司会者は答えを知っているので確実にはずれのドアを開けます。最初に選んだドアが当たりの場合、選ばなかった2つのドアからランダムで片方のをドアを開けます。
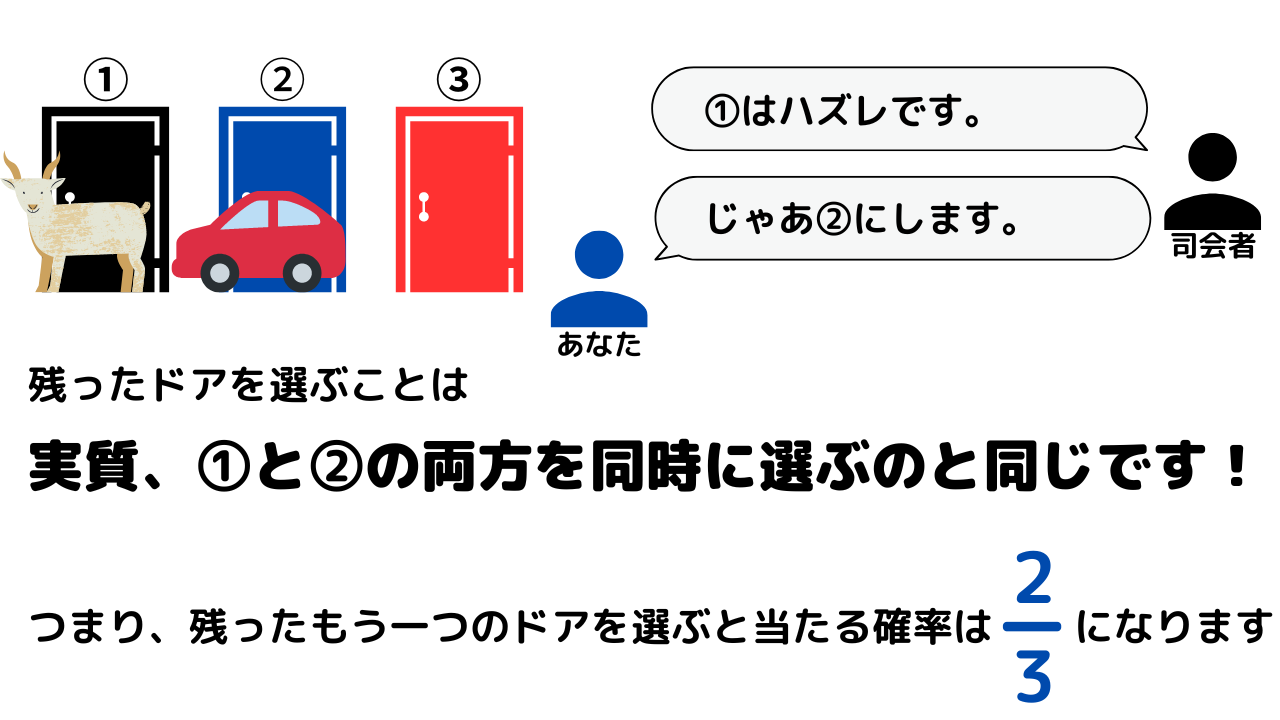
司会者は「ドアを変更しますか?」と聞いてくるのですが、もしドアを変更した場合、実質2つのドアを開けることになります。
最初に選んだドアが当たりの確率は\(\frac{1}{3}\)から変わりませんが、残った最後のドアが当たりの確率は\(\frac{2}{3}\)になっているのです。



最初に司会者がはずれを1つ見せます。
さあ、残った2つのうちどちらを選んだ方がいいか?
と聞かれたら、そりゃ\(\frac{1}{2}\)です。



そこから変わるわけないですよね?
簡潔に
司会者がはずれのドアを開けたら、残りのドアは2つだから確率は50%じゃね?
じゃないのよ。
最初に選んだドアが当たりなのは\(\frac{1}{3}\)で、残りの2つのどちらかが当たりの確率が\(\frac{2}{3}\)。
残りの2つのうちの片方がはずれだと分かったら、残った最後のドアが当たりの確率が\(\frac{2}{3}\)になる。
最初に選んだ\(\frac{1}{3}\)のドアよりも、最後に残った\(\frac{2}{3}\)のドアを選んだ方が良いよねって話。
ドアを100個にする説明
モンティホール問題のよくある説明で、「ドアが3個ではなく100個の場合を考えよう!」というものがあります。
ドアが100個あります。当たりは1つです。
あなたが1つドアを選びます。
司会者が残りの99個の内、98個のドアを開けてはずれだと示します。
さあ、今選んでいるドアと残ったドア、どっちの方が当たる確率が高いでしょうか?
というものです。
なんで98個も開けてるねーんというツッコミはさておき、ここまで極端な例を出されたら、流石に最後の2つのドアの価値が等しくないって分かりますよね。
最初に選んだドアが当たりの確率は1%ですが、残ったドアが当たりの確率はめっちゃ高いです。
これと同じ現象がドア3つのモンティホール問題で起こっているのです。
まとめ
分かりやすく説明できていたでしょうか?
モンティホール問題は納得できない人が多い問題であるため、ある程度解説しても納得できない人は多いままなのではないかと思います。
1対1で会話をしながらであれば簡単に説明できるのですが、サイト上だと、読者の理解できていない部分が分からないので難しいです。
様々な説明が各サイトで行われているので、この記事だけでは分からなかった人は他のサイトを参考にしてみてください。
もちろん、コメント等での質問を行っても良きです。












