・重力とは
・張力とは
・垂直抗力とは
・弾性力とは
力学の目的は「物体の位置と速度」を求めることです。
位置を求めるためには速度が必要であり、速度を求めるためには加速度が必要であるため、前回と前々回で加速度について学習しました。
これで力学は終了!
と言いたいところなのですが、物体の加速度の値はどうやって求めればいいのでしょうか?
今回は、物体の加速度を求めるために必要な「力」というものについて説明をしたいと思います。
力とは
物体を加速させたり、変形させたりするもの。
力の単位は全て[N](ニュートン)。
その向きと大きさを矢印で表す。
力とは”物体を加速させたり変形したりするもの”のことをいいます。
物理基礎では物体の形が変わることを考えないので、物体を加速させるもののこと、つまり、物体を動かすようなもののことを力と呼ぶことにします。
物理には色々な力が登場するので、どんな力があるのか1つ1つ覚えていきましょう。
重力と質量
地球から引っ張られる力。重さとも言う。
質量mが大きいほど重力も大きくなる。
$$W=mg$$
物体固有の量、場所によって変化しない。
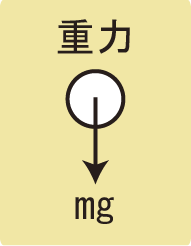
地球に引っ張られる力のことを重力といい、記号Wで表します。Weightの頭文字ですね。
図で表すときは、物体の中心(重心)から下向きに矢印を描きます。
重力は質量m [kg]と重力加速度g [m/s2]に比例するので、mg [N]で表されます。
力の単位は全てニュートンNなので、単位はもちろん[N]です。
一方、質量とは物体固有の量のことを言います。記号はmで表し、単位は[kg]です。massの頭文字ですね。
「重力と質量って何か違うの?」
と思うかもしれませんが、重力と質量は同じではないため、重力と質量の違いについても詳しく説明します。
重力(重さ)と質量の違いは何か
宇宙空間のような無重力の世界には「重さ」というものは存在しません。
宇宙では身体が浮くイメージがありますが、宇宙では重力が存在せず、重さが0Nとなってしまいます。
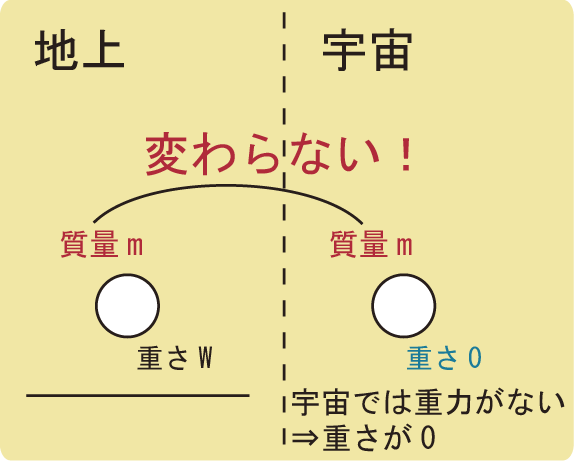
しかし、重さがなくなっても体の肉や骨は存在しているので質量は0kgになりません。
このような、地球でも宇宙でも変わらないような物質の量のことを質量と呼びます。
ボールやお米など、物体に対しては質量という言葉を使うのですが、人間に対しては質量という言葉ではなく体重という言葉を使います。
そのせいでよく勘違いしてしまうようですが、体重とは質量のことであり、重さではありません。
体重が60kgである人の質量は60kgですが、重さは60kgではないのです。
じゃあ体重60kgの人の重さはどれくらいなの??
というと、公式W=mgを使います。
Wが重力(重さ)、mが質量、gが重力加速度(地球では9.8m/s2)なので、
\begin{eqnarray}
W&=&mg\\
W&=&60×9.8\\
W&=&588
\end{eqnarray}
となります。
体重という言葉から重さというものをイメージしてしまいますが、体重の単位は[kg]であるため、体重は重さではなく質量であるということを勘違いしないようにしましょう。
また、重力はWであると説明したのですが、公式W=mgという式があるためWよりもmgを使って表すことが圧倒的に多いです。
重力Wとは言わず、重力mgと言うことの方が多いので、重力といったらmgと覚えておきましょう。
重力は月や宇宙に行くと変化するが、質量は月や宇宙でも変わらない
体重は重さではなく質量のこと
張力とは
糸が引っ張る力。
糸があったら必ずTを使うと考えよう。
糸が引っ張る力のことを張力といい、記号はTを使います。もちろん単位は[N]です。
Tはtensionの頭文字です。tensionは緊張という意味であり、糸がピンと張っている状態が緊張状態であることからTという記号を使います。
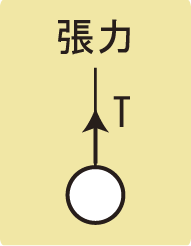
糸がピンと張っているとき、糸が物体を引っ張る方向に矢印を描きます。
糸と物体がくっついているところが矢印のスタート地点です。
図に糸がある場合、ほぼ100%の確率で張力が関係している問題なので、糸があるかどうかを必ず確認しましょう。
糸があったら張力T[N]を絶対に使う!
と思っておくこと
垂直抗力とは
壁や地面など、面から受ける垂直な力。
垂直抗力がない=面と触れていない(もしくは、面から離れる瞬間) ということ。
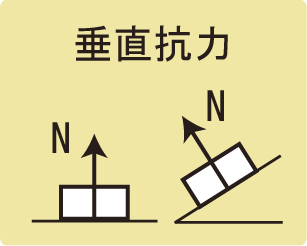
面から受ける垂直な力のことを垂直抗力と言います。記号はNで、単位も[N]です。
垂直抗力のNはNormal forceの頭文字のNになります。私たちは垂直に立っていることが普通なので、垂直はノーマルということですね。
垂直抗力は面(主に地面や壁)から受ける力なので、垂直抗力が0ということは地面とくっついていない(離れる瞬間を含む)ということです。
「地面から離れるときの○○を求めよ」と聞かれたときは、垂直抗力N=0としましょう。
垂直抗力は地面や坂から垂直な力
地面から離れるとき、垂直抗力N=0となる。
弾性力とは フックの法則と公式
バネやゴムが元に戻ろうとする力。
自然の長さ(元の長さ)から伸び縮みした長さと弾性力は比例すること。
$$f=kx$$
f…弾性力[N]
k…バネ定数[N/m]
x…バネの伸び縮み[m]
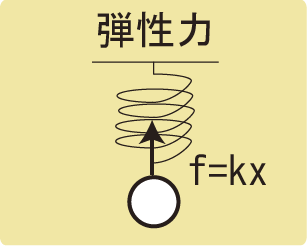
バネやゴムが元に戻ろうとする力を弾性力といい、記号はf(大文字のときもある)、単位は[N]で表します。
fはforceの頭文字です。forceは力という意味であり、その他の力は全部fで表します。
バネやゴムは、伸ばせば伸ばすほど元に戻ろうとする力も大きくなります。
2倍長く伸ばせば、元に戻ろうとする力も2倍に
3倍長く伸ばせば、元に戻ろうとする力も3倍になります。
このような関係を比例関係と言い、バネの弾性力と伸び縮みした長さは比例するという法則をフックの法則と言います。
中学校1年生の数学では、比例の簡単な例として
$$y=ax$$
という式を習います。
比例の式では
\begin{cases}
y…変数\\
a…定数\\
x…変数
\end{cases}
のように、変化する数2つと、決まった数が1つありますよね。
$$フックの法則 f=kx$$
では、
\begin{cases}
f…変数\\
k…定数\\
x…変数
\end{cases}
となっており、このときの定数kのことをバネ定数といいます。
バネ定数kはバネによって決まっている値であり、バネの計算をするとき以外には出てきません。
とりあえず、kがバネ定数だと覚えておけば大丈夫です。
まとめ
物理では様々な力が登場します。
今回勉強した重力、張力、垂直抗力、弾性力だけではなく、
摩擦力、浮力、万有引力、遠心力、静電気力、磁力など、様々です。
力は目に見えないため、どんな力がはたらいているのか想像するしかありません。
力がどのようにはたらくのか、少しずつ慣れていきましょう。
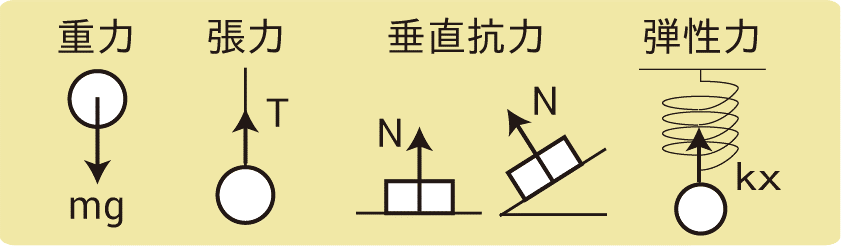
また、力は全てベクトル(矢印)で表すので、どこから始まっているのか(重力なら重心、糸やバネは接触している部分、垂直抗力なら面)と大きさ(矢印の長さ)を正しく描くことを心がけましょう。












