・力の合成と分解とは
前回と前々回で色々な力について紹介しました。
重力，張力，垂直抗力，弾性力，浮力がそれぞれ何の記号で表され，どのような公式があったか覚えていますか？
勉強ができるようになる秘訣は，一度見た内容を忘れないように思い出すことです。
もし忘れている場合は，軽くでもいいのでもう一度読み直してみましょう。
力は「向き＋大きさ」のベクトル(矢印で表すもの)なので，合成と分解をすることができます。
中学三年生の理科の内容でもあるので，知っている人も多いかもしれませんね。
今回は，力の合成と分解について，わかりやすく簡単に解説をしていきます。
力の合成とは
複数の力を1つの力として扱うこと。合成した力のことを合力という。
2つの力を合成した場合，合力は平行四辺形の対角線の大きさと向きとなる。
力の合成とは，物体に複数の力がはたらいているとき，複数の力を合わせて1つの力とすることです。
また，1つに合わさった力のことを合力といいます。
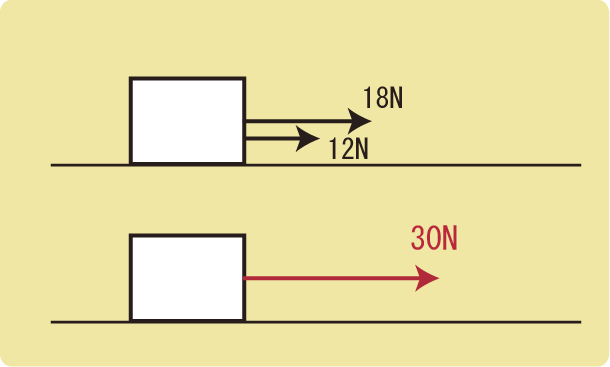
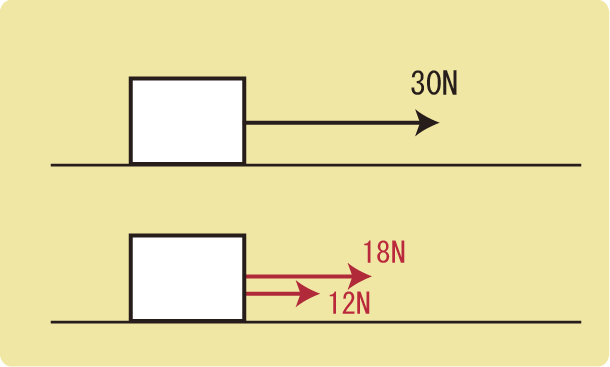
例えば，物体に18Nと12Nの力がはたらいているとします。
物体には2つの力がはたらいているのですが，この2つの力を合わせて30Nの力とすることができます。
これが力の合成です。
引っ張られる側からすると，18Nと12Nの力で同時に引っ張られることと，30Nの力で引っ張られることの違いを感じることができないため，力の合成をすることができるということになっています。
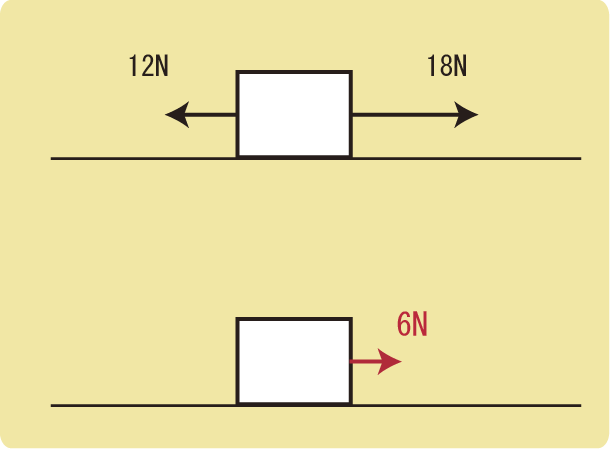
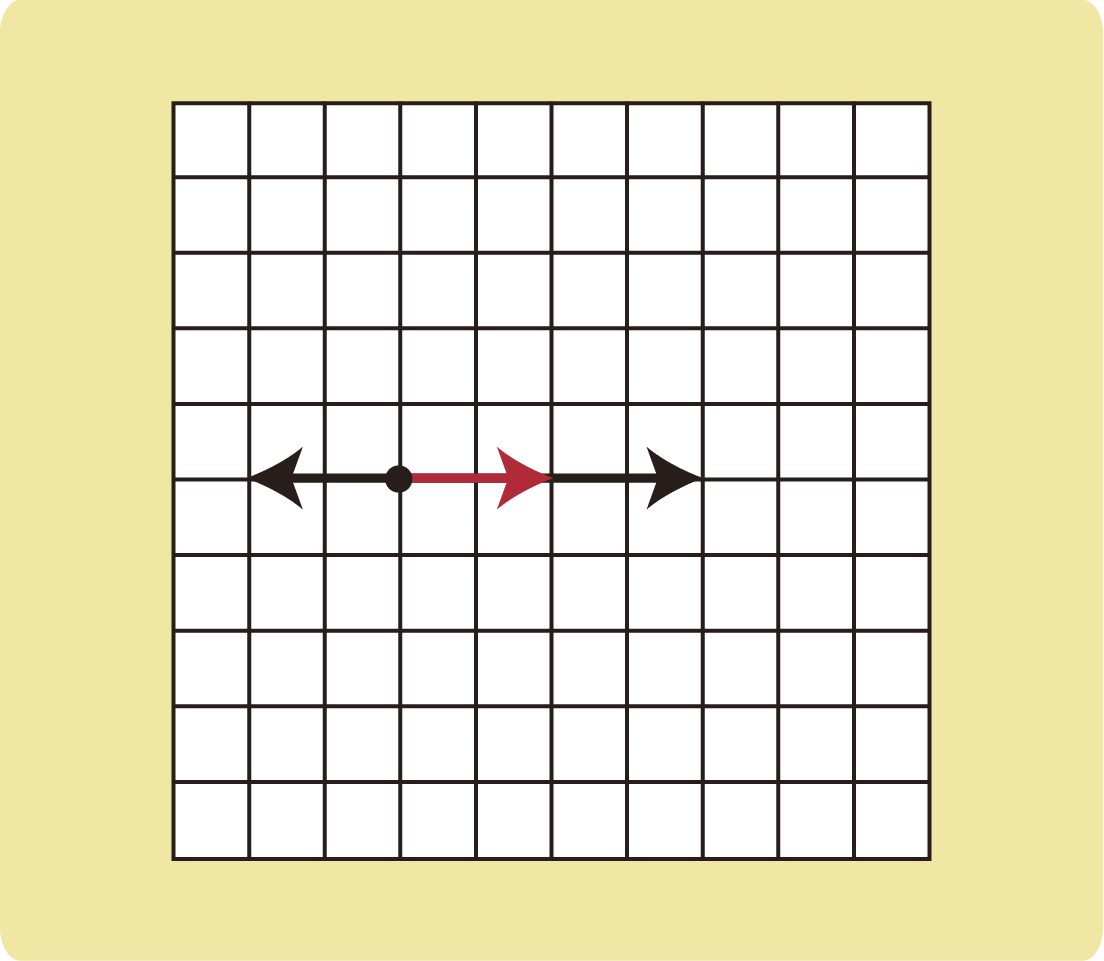
力はベクトルであるので，単純な数字の足し算とは限りません。
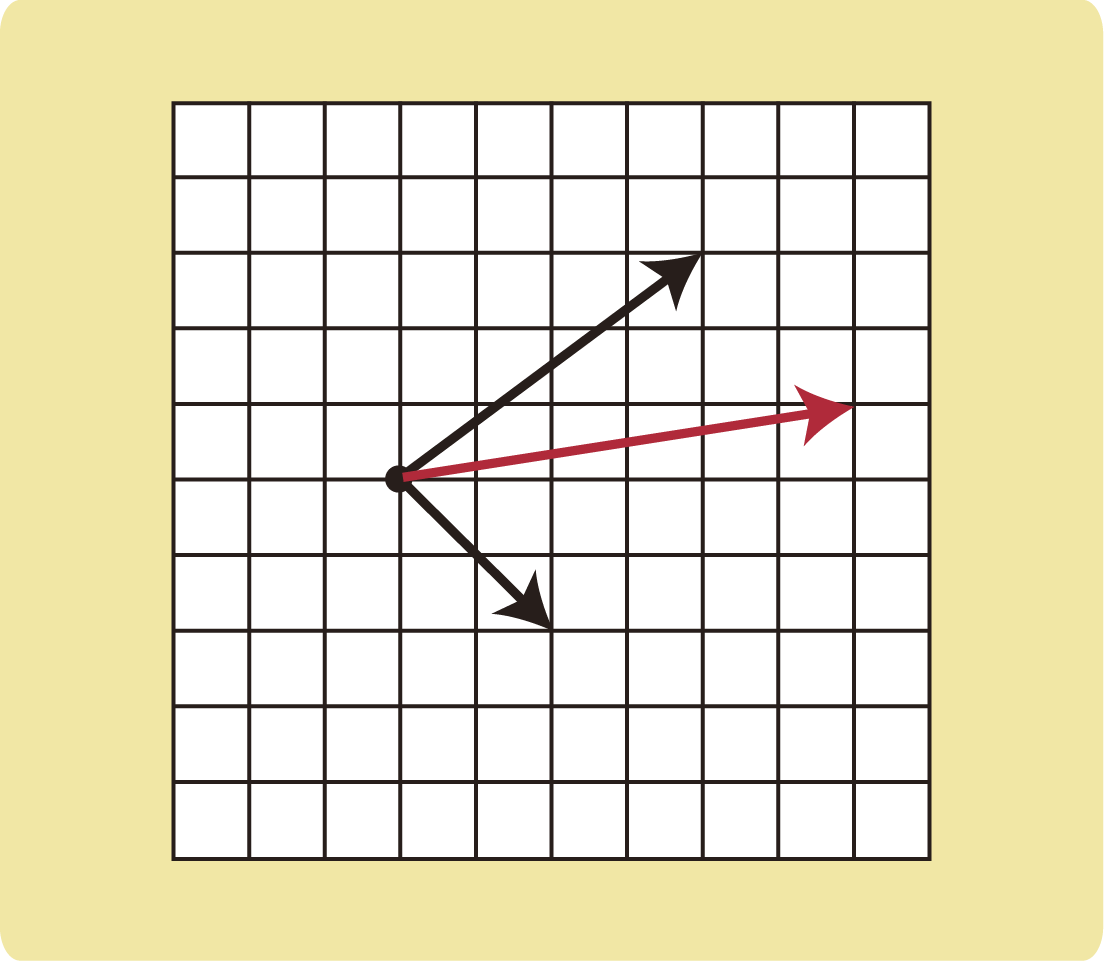
力の方向が逆向きであれば，引き算になるかもしれませんし(+と－の足し算)，2つの力が同じ向きでも逆向きでもない場合，合力の向きと大きさは，2つの力の矢印が辺となっている平行四辺形の対角線の向きと大きさになります。
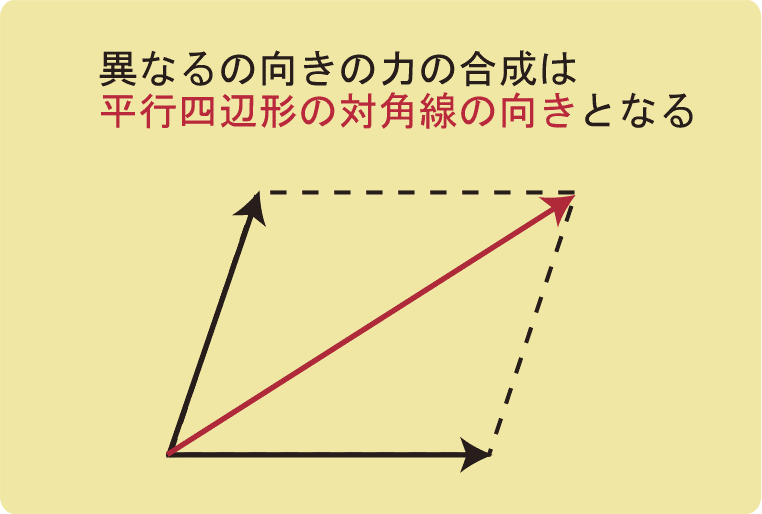
実際に，図のような2つの力で引っ張ると，図の赤い矢印の向きに物体が動きます。
スマホを手に取って上向きの力と右向きの力を同時に加えてみてください。右上に動きましたよね？
右上に引っ張ることと，上と右に同時に引っ張ることは同じなのです。
同じ方向か，逆向きの方向であれば力の合成をすることが多いため，一直線上であれば力の合成を使うかもしれないと考えましょう。
また，合成することができるということは分解することもできます。
むしろ，力の合成より力の分解の方がよく使うので，今回の内容は力の分解がメインとも言えます。
とりあえず，力の合成の例題を解いてみましょう。
例題
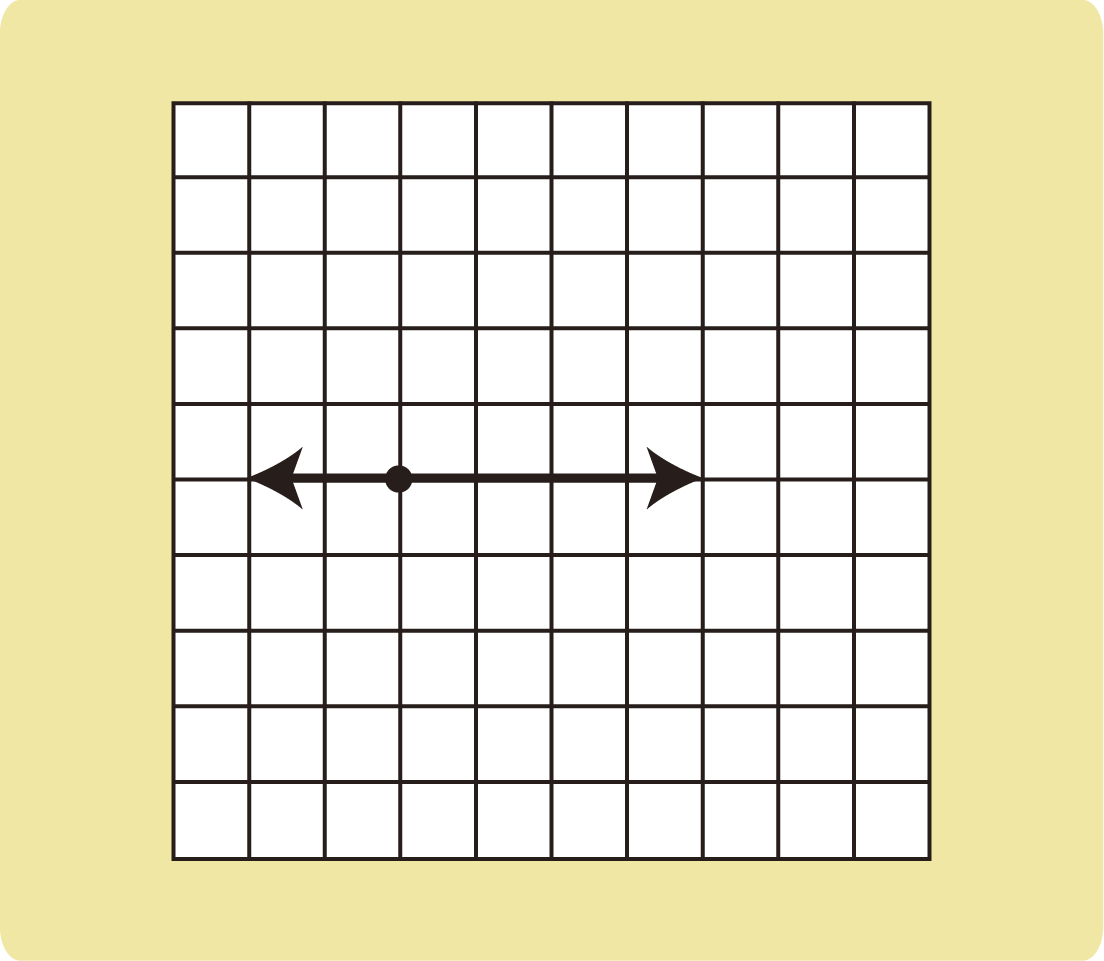
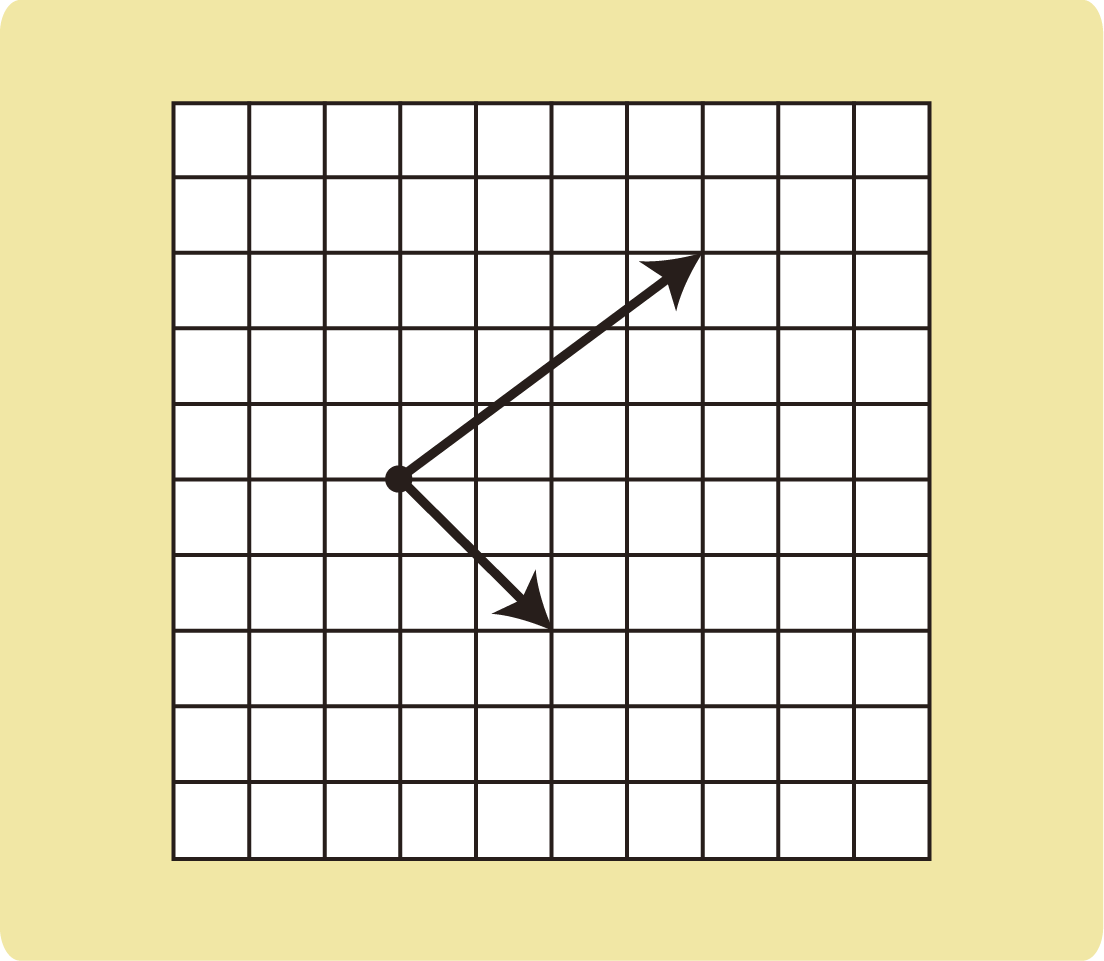
例題1
図の2つの力の合力を図示せよ。
(1)
(2)
同一直線上であればそのまま足し，同一直線上でないのであれば平行四辺形の対角線の向きに合成する。
(1)
(2)
力の分解とは
1つの力を複数の力に分けること。
力の分解とは，1つの力を複数の力に分けることです。
複数の力に分けられたそれぞれの力のことを分力と言います。
力の分解の考え方は，力の合成の逆です。
力の合成とは反対に，1つの力を複数の力に分けるという考えが力の分解です。
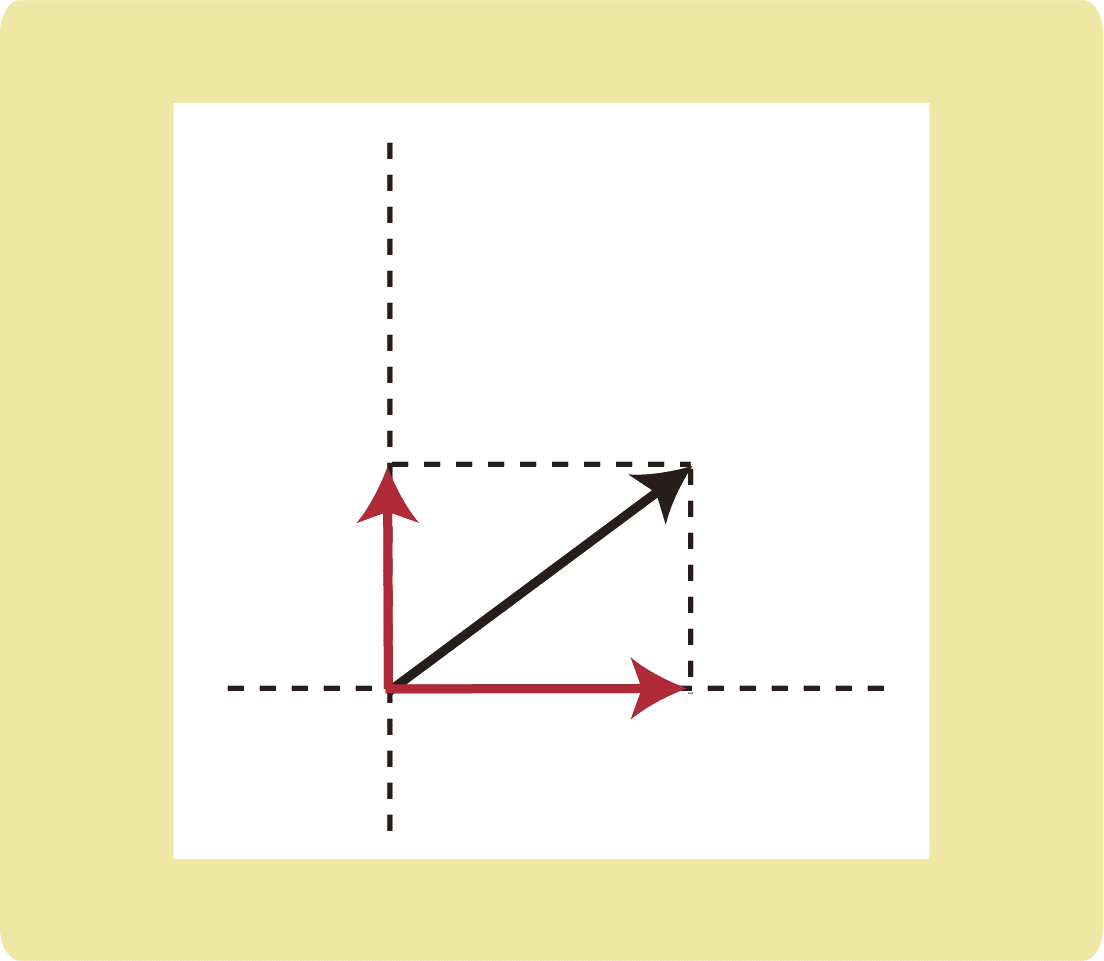
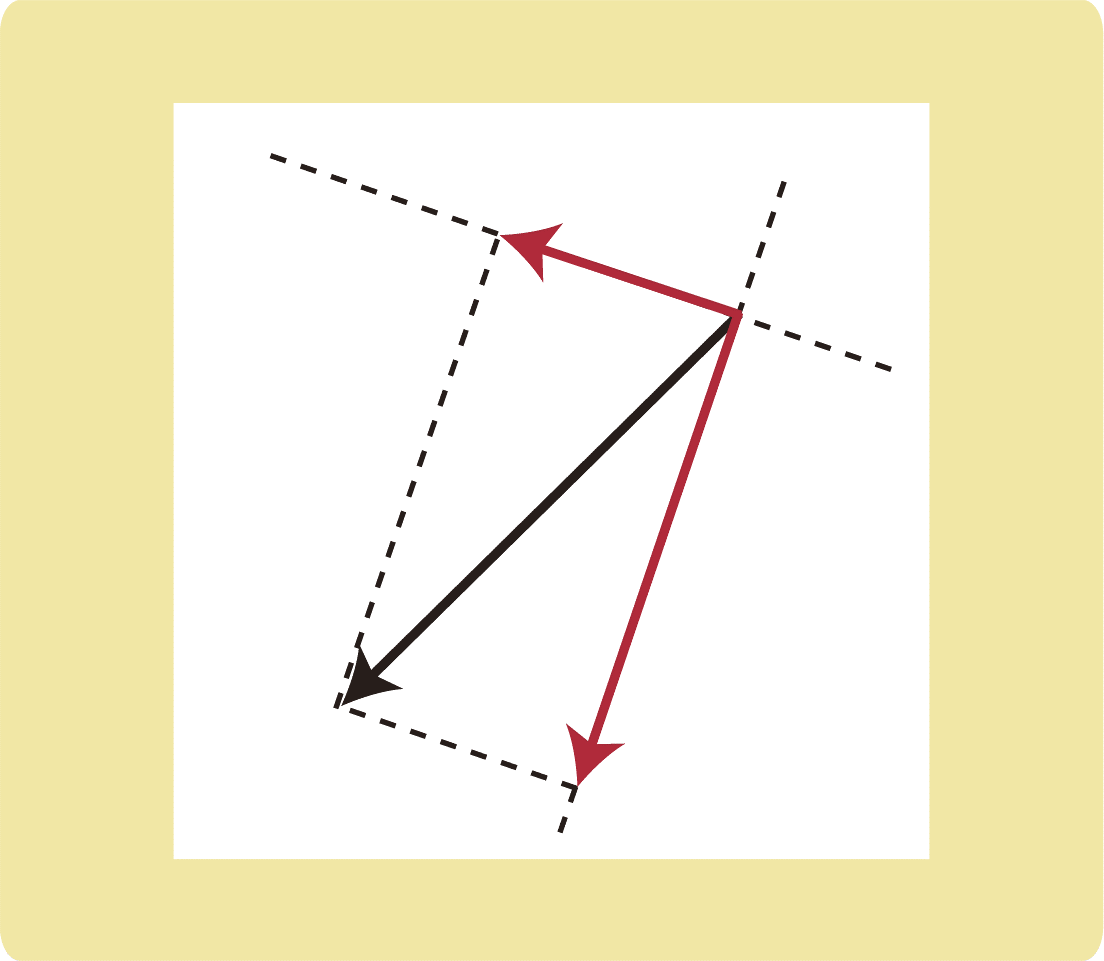
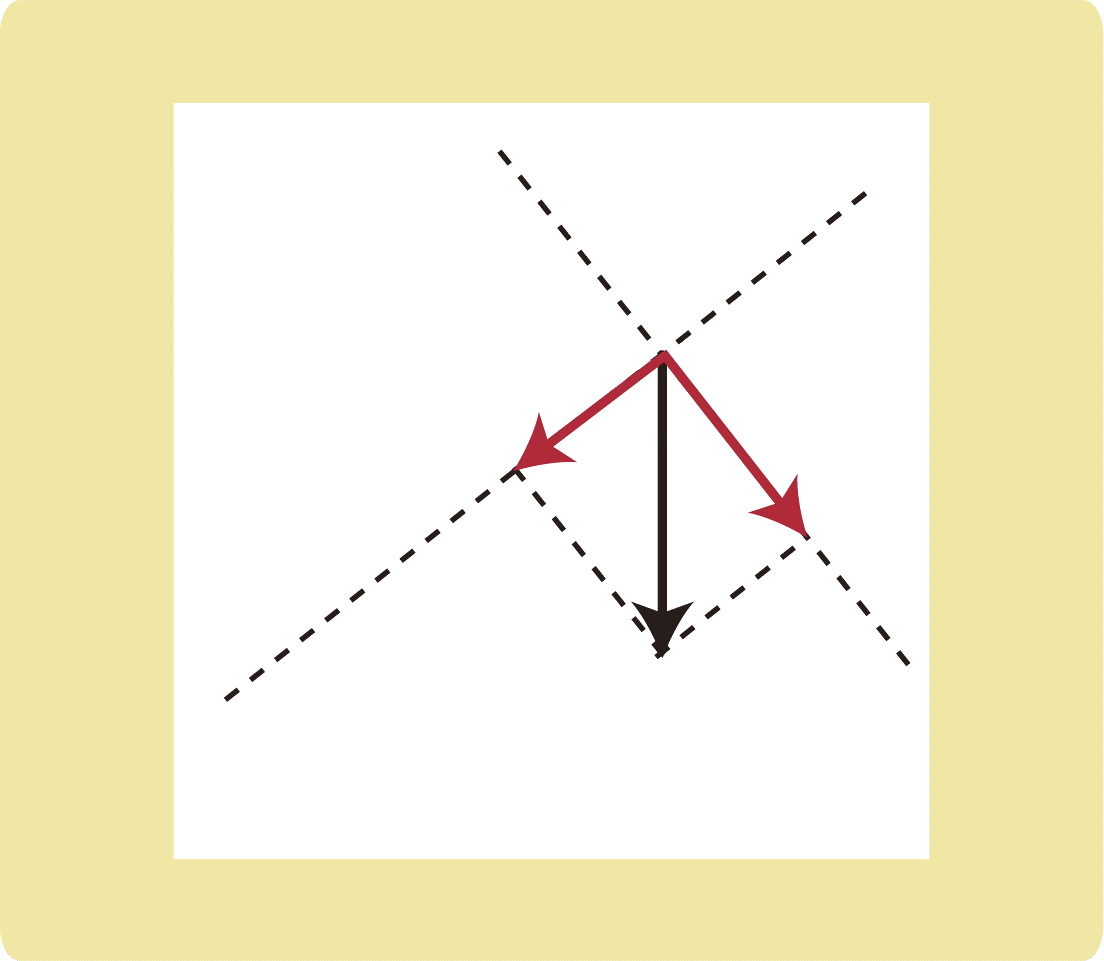
しかし，図のように力を分解することはまずありません。
物理では，斜め向きの力をよく分解します。
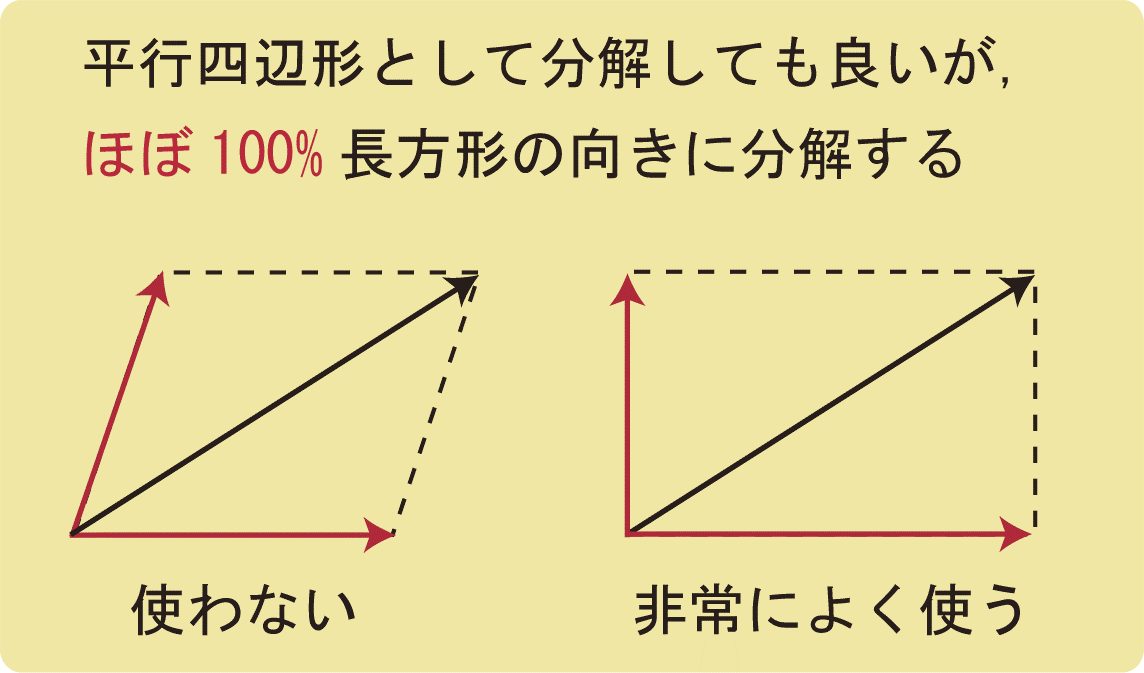
斜め方向の力は分かりにくいため，上下左右に分解して考えることが多いです。
このとき，平行四辺形のように分解しても斜め向きの力がまた現れるだけなので，分解するときは長方形の向きに分解をします。
さらに，物理基礎の簡単な問題では，力の分解をするときに30° 45° 60°の直角三角形を使うことが多々あります。
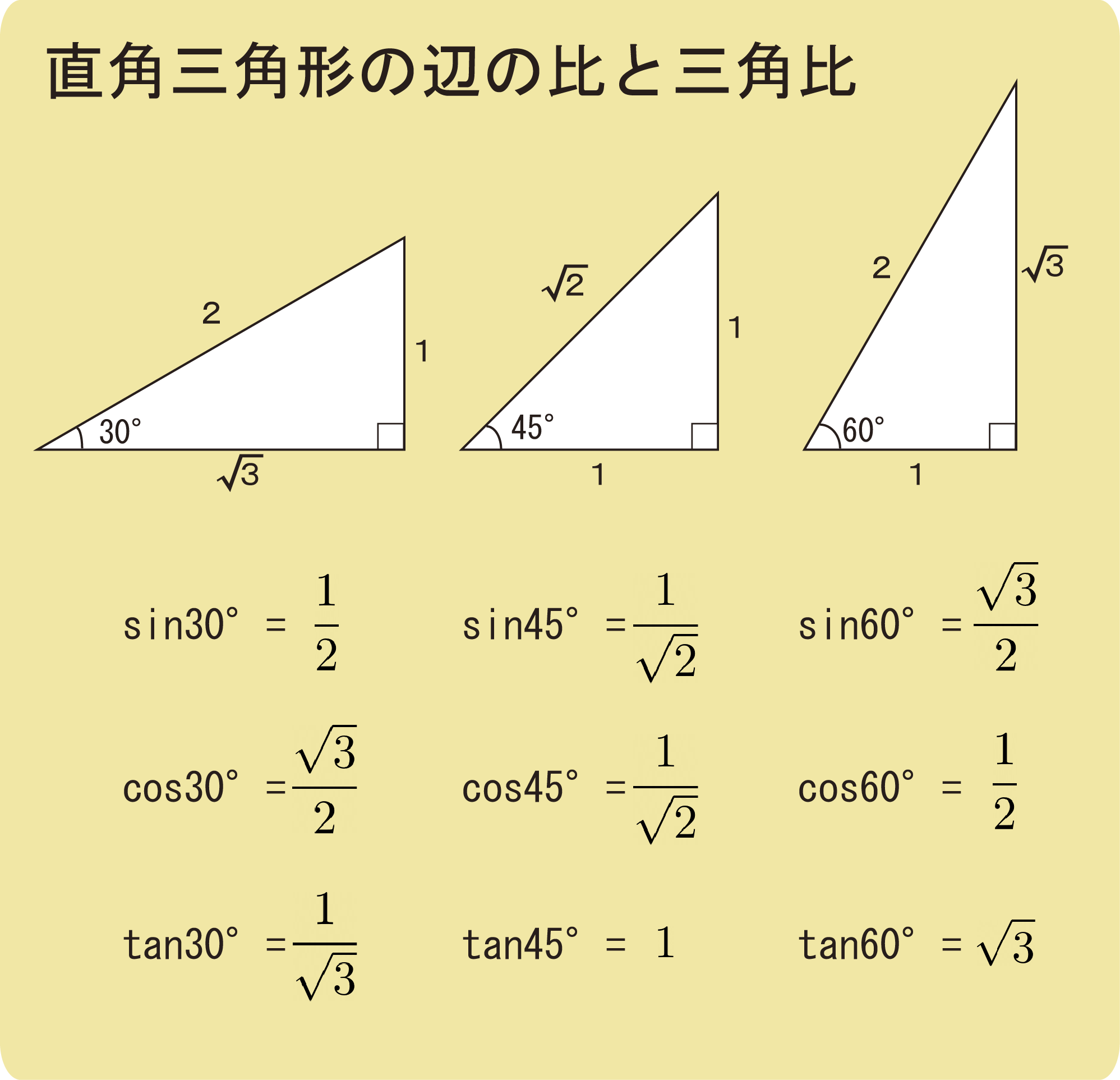
これは物理ではなく数学の範囲なのですが，物理や物理基礎で非常によく使う内容なので，必ず覚えておきましょう。
sinやcosを習っていない場合は，三角形の辺の比だけを覚えておけば大丈夫です。
例題
例題2
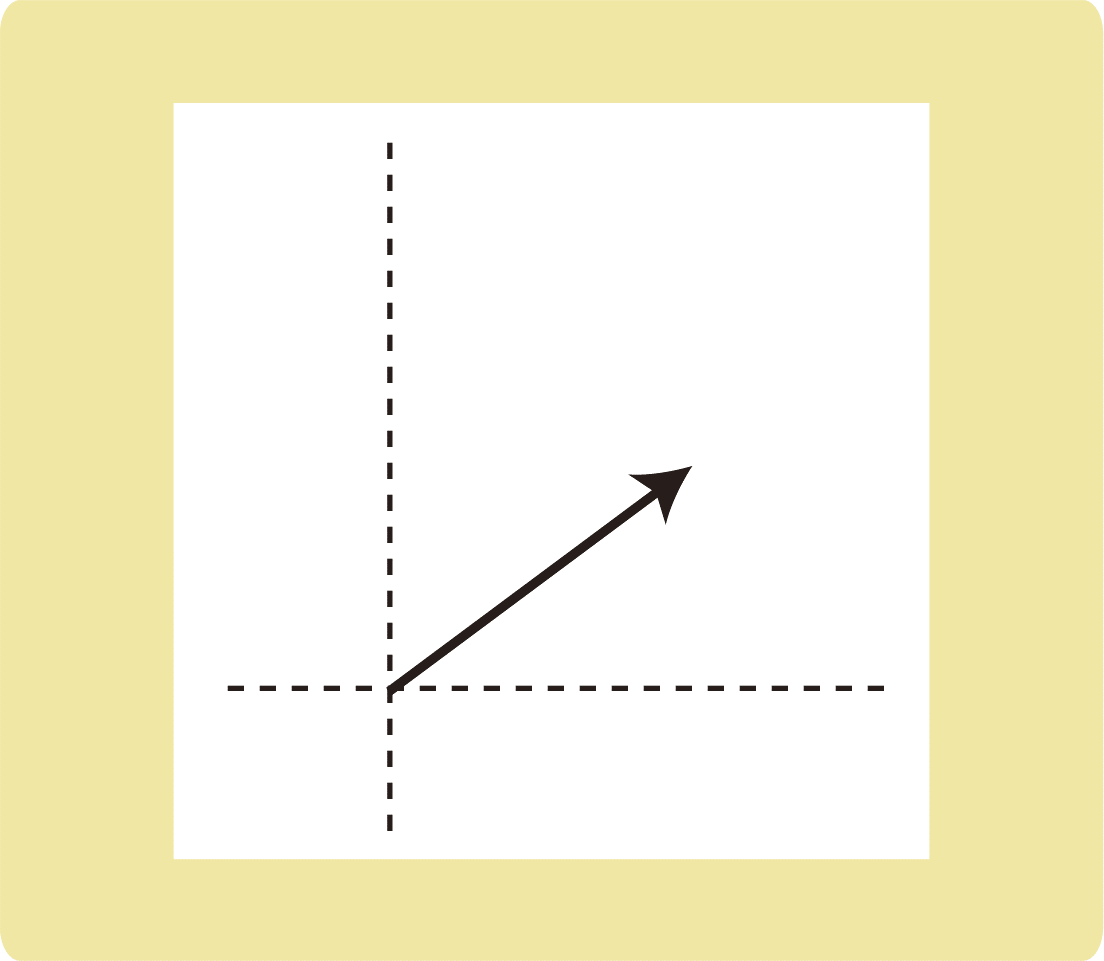
次の図に示された力を，破線の方向に分解し，図示せよ。
(1)
(2)
(3)
破線で長方形を作り，その長さの矢印をそれぞれ描きましょう。
(1)
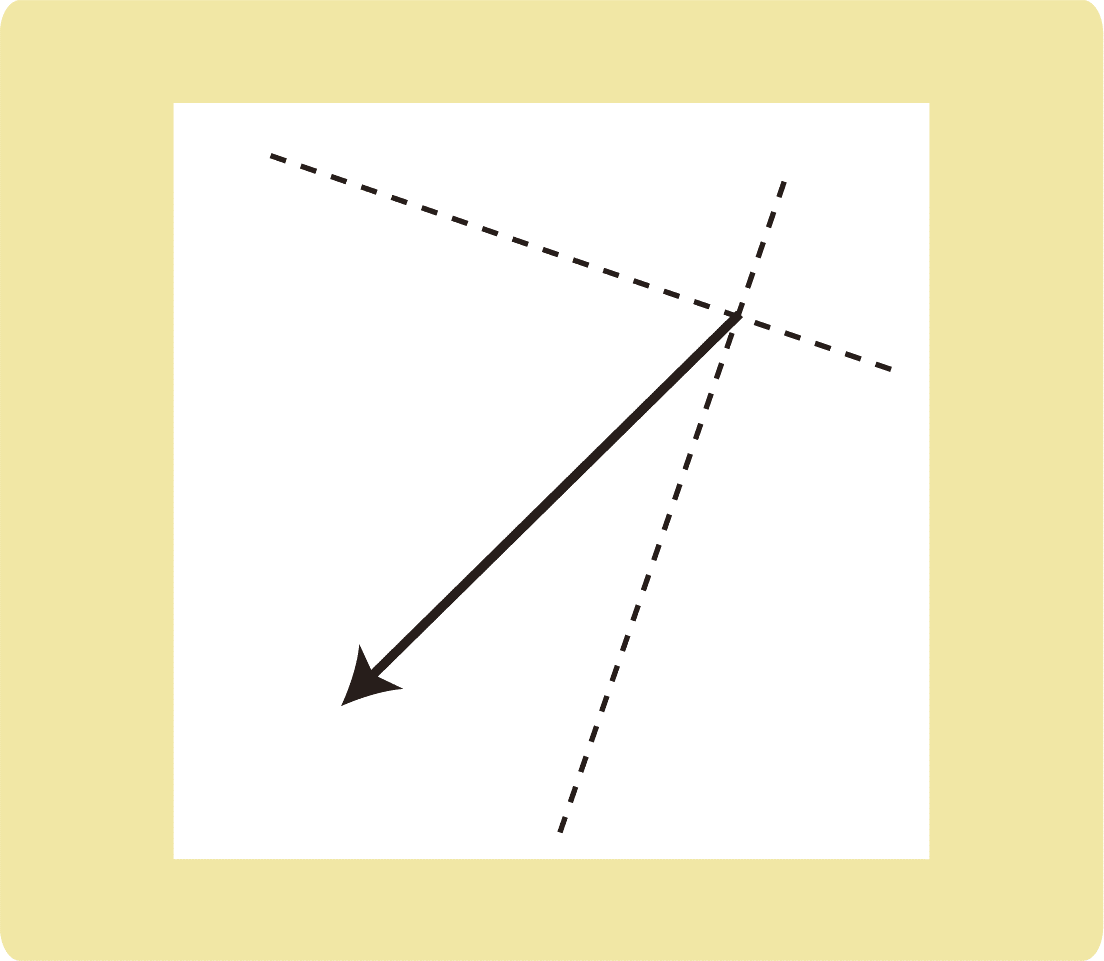
(2)
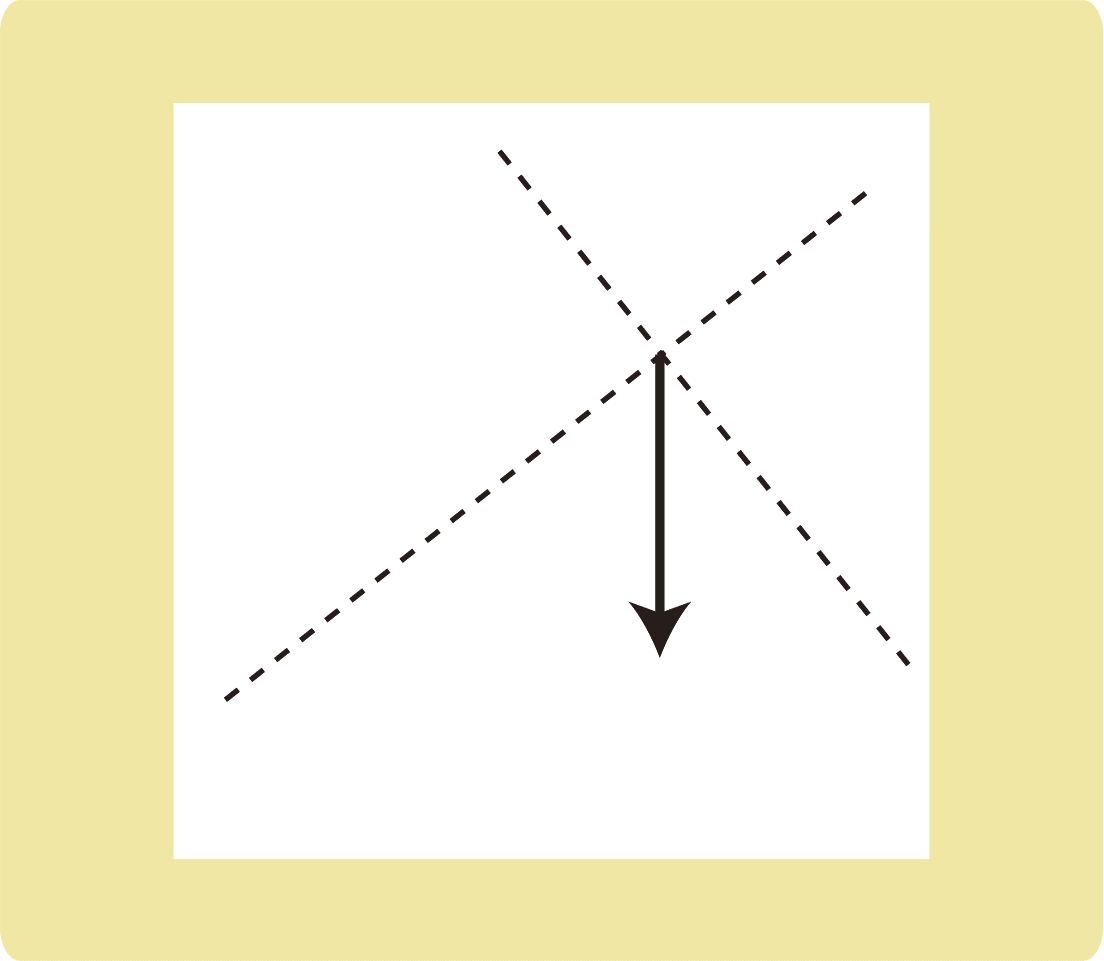
(3)
例題3
図の力のx成分とy成分はそれぞれ何Nになるか。
(1)
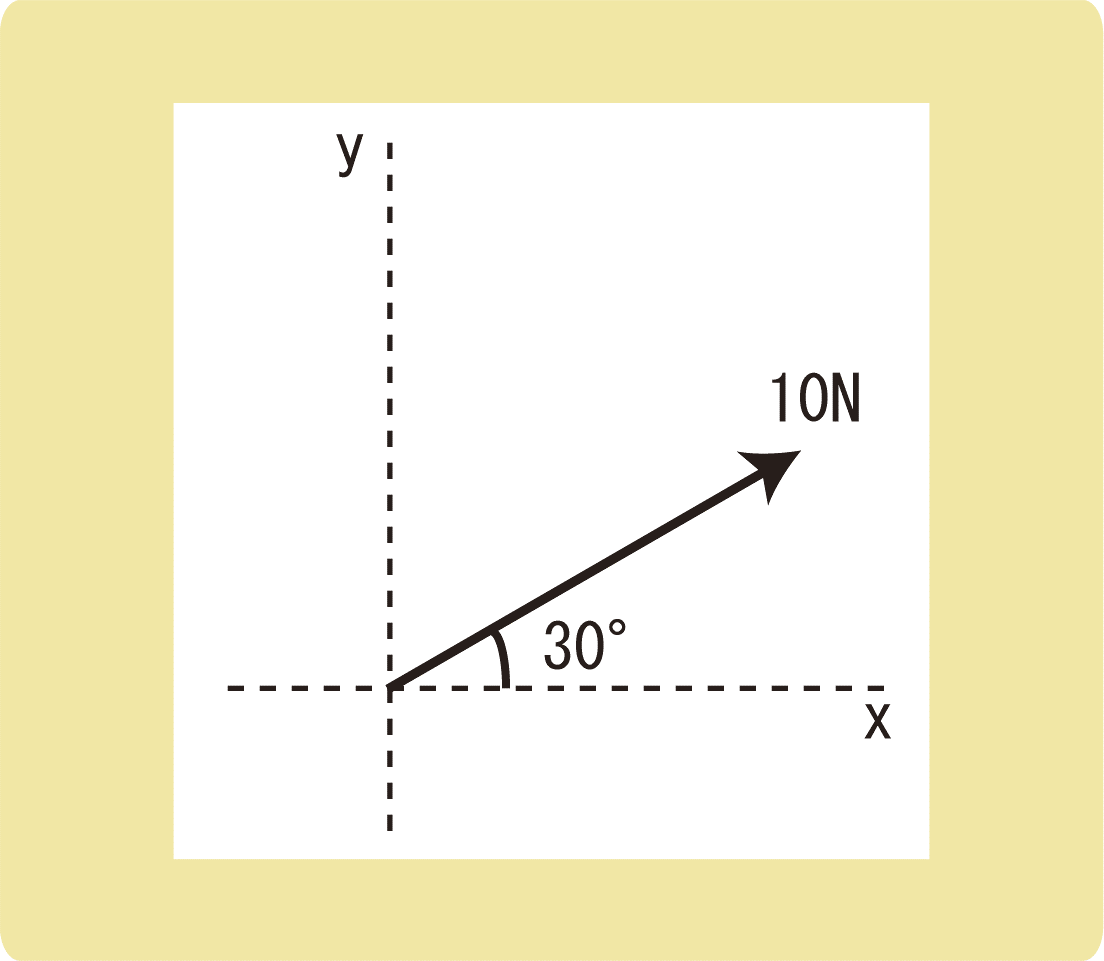
(2)
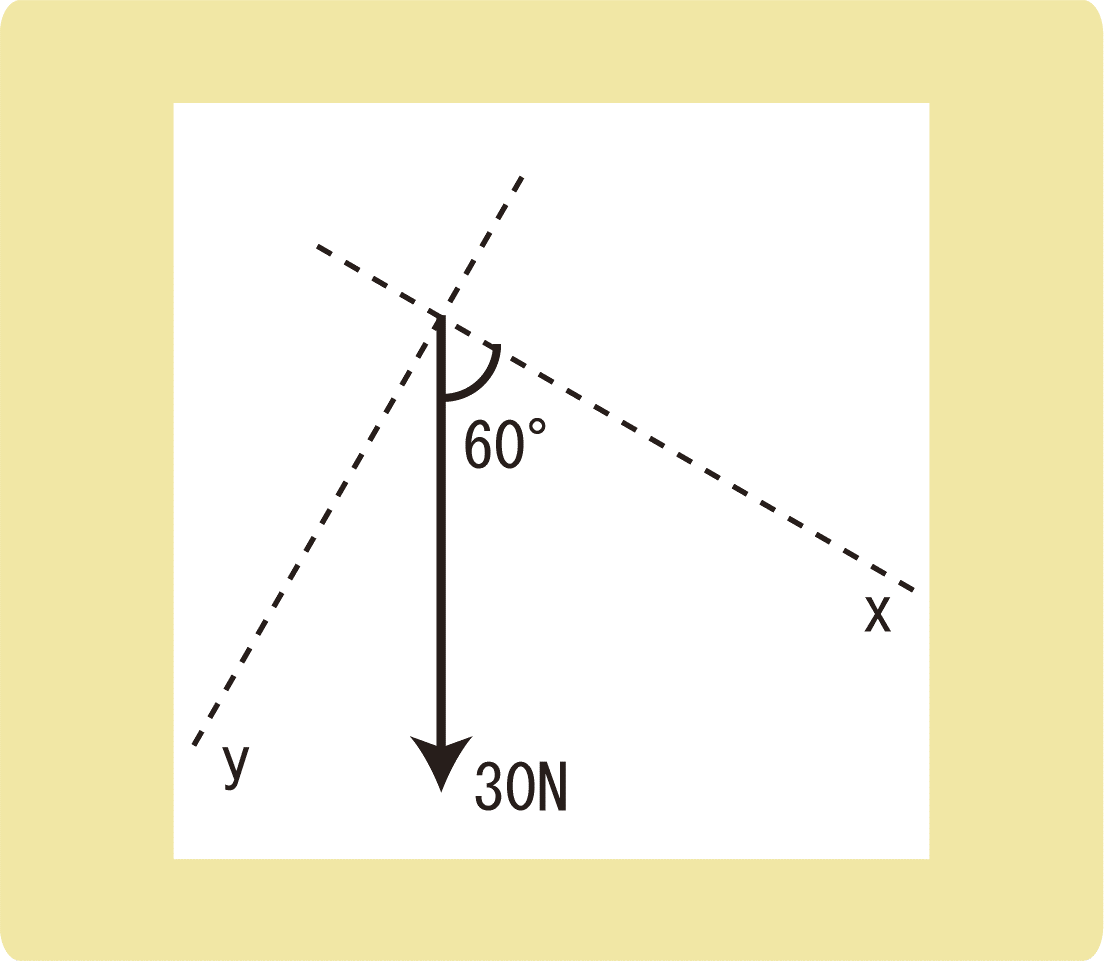
まとめ
力はベクトルなので，合成と分解をすることができます。
合成するときは平行四辺形の対角線になるように合成をしましょう。
分解するときは色々な四角形に分解することができますが，長方形以外の形で分解することはまずありません。
分解したとき，角度が分かっていればsinとcosを使います。θの付いている方がcosであると考えると分かりやすいです。
力の分解はこの先の分野でも必ず必要になってくる考えなので，必ずできるようにしておきましょう。
