周期・振動数・波の基本式とは

前回に引き続き、今回も波に関する基本的な用語を、可能な限りわかりやすく簡単に解説していきます。
今回説明する「振動数・周期・波の基本式」は他の分野でも使う重要な内容なので、しっかり理解しておきたいです。

まずは、波の基本的な用語の説明の続きをします。

連続波とパルス波とは

連続波とは、その名の通り連続的に波源を振動させてできた波です。

上図が連続波です。波がずーっと現れては進んでいくイメージですね。

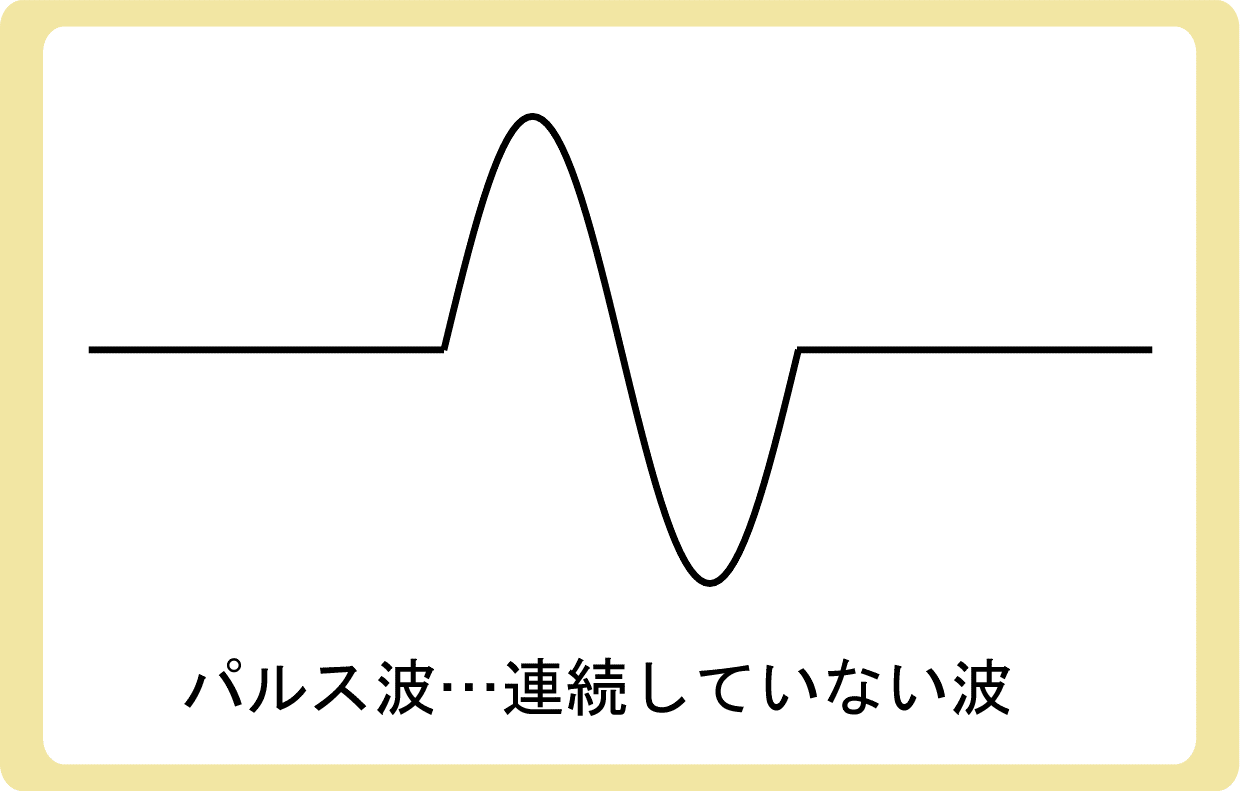
一方、パルス波とは、断続的に振動するような孤立した波のことを言います。連続していない波がパルス波です。

周期とは

周期とは、1回振動するのにかかる時間のことで、記号はT、単位は秒［s］で表します。
「1回に何秒かかるか」ということが周期であるため、「地球の公転周期」「潮汐の周期」「月経の周期」と日常生活で使うこともありますよね。

周期は英語でperiodですが、時間を表すので大文字のTを使います。
計算は非常に単純で、5回振動するのに50秒かかれば、周期T=10秒となります。

振動数とは

振動数とは、1秒間に振動する回数のことです。
記号はfrequencyの頭文字のfを使い、単位は［Hz］(ヘルツ)です。

楽器を習っている人や、音楽系の部活に入っている人は必ず知っていると思いますが、ラの音は440Hzですよね。(吹奏楽だと442Hzに合わせることが多いです)

「440Hzとは、1秒間に440回揺れていること」なので、喉を1秒間に440回揺らすことでラの音を出すことができます。

周期と振動数の公式

周期と振動数の説明が似ていることに気が付きましたか？

・周期T［s］…1回振動するのにかかる時間

・振動数f［Hz］…1秒間に振動する回数

周期は1回にT秒、振動数は1秒でf回
という、反対の説明になっていますよね。
これを比で表すと

$$1回：T秒＝f回：1秒\\
T×f=1×1\\
f=\frac{1}{T}$$

となります。
これが周期と振動数の関係の公式です。

波の基本式とは

波の基本式は、波動の分野の中で最もよく使う重要な公式です。

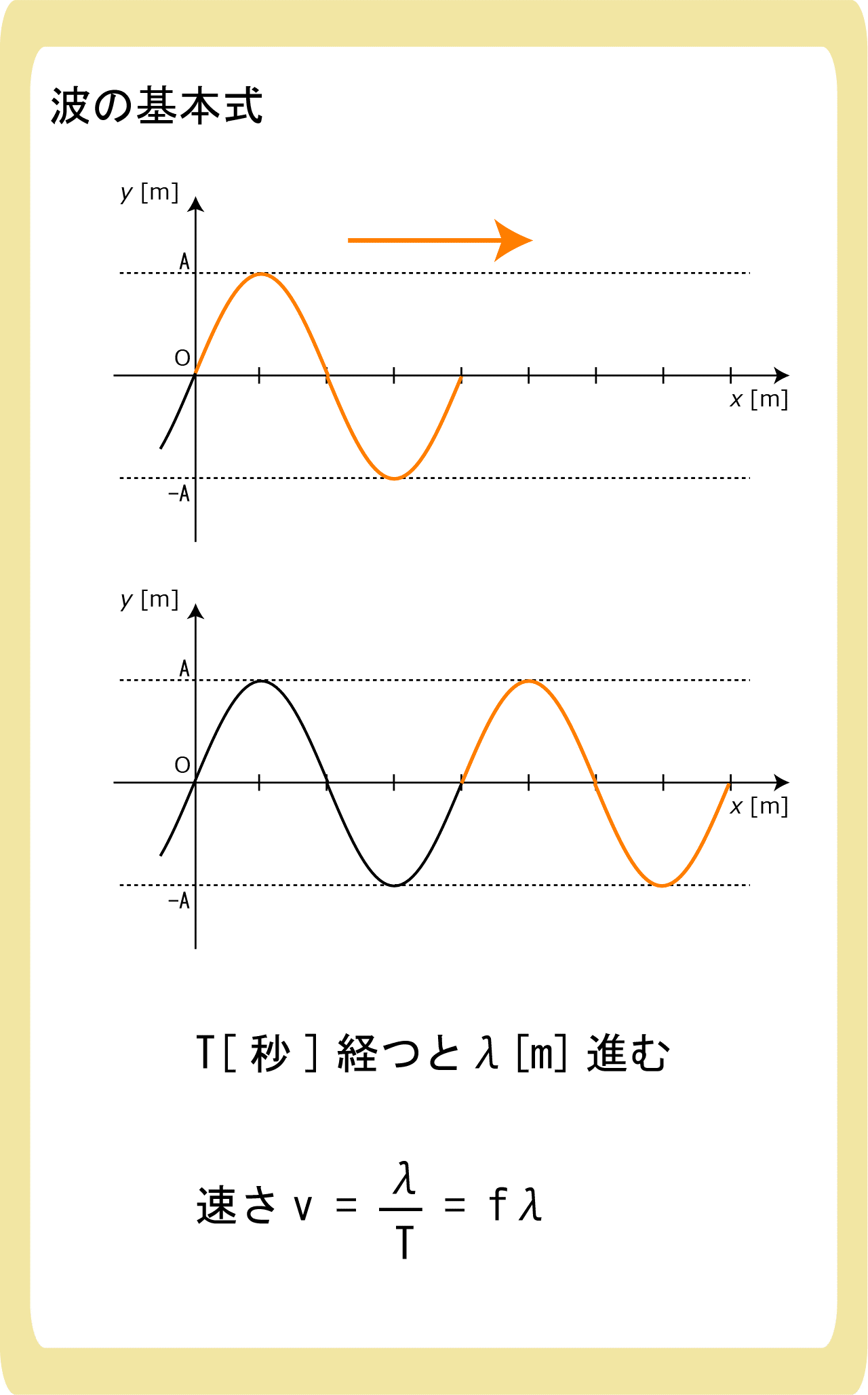
図のような、右に進む連続波を考えてみます。

オレンジ色で表した部分は波長なので、長さはλ[m]です。
周期T[秒]とは1回振動するのにかかる時間なので、T[秒]経つと波1つ分であるλ[m]進んでいることになります。

波の速さが一定であるとすると、

$$速さ=\frac{距離}{時間}$$

なので、

$$v=\frac{λ}{T}$$

となります。

ここで、

$$f=\frac{1}{T}$$

を使うことで

$$v=fλ$$

という式を求めることができます。

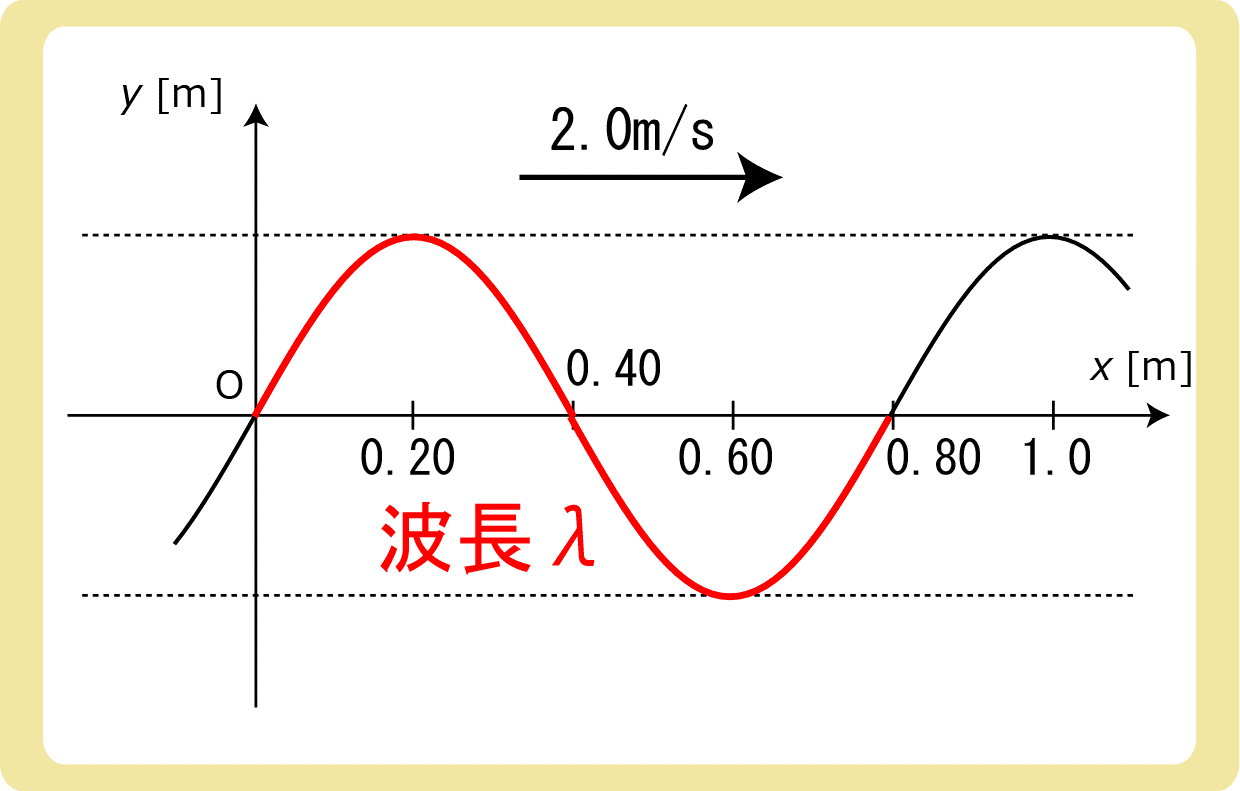
例題

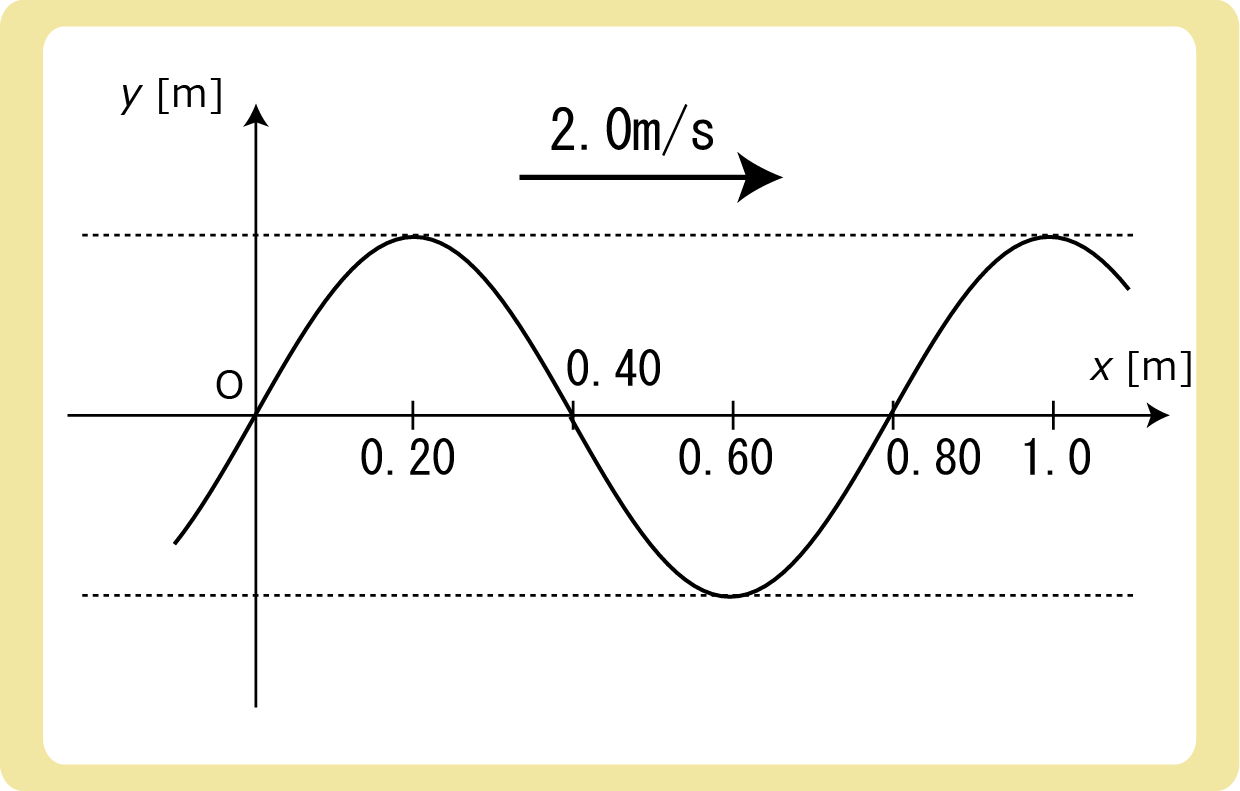
図のような正弦波が、x軸正の向きに2.0m/sの速さで進んでいる。次の各問に答えなさい。
(1)この波の波長は何ｍか。
(2)この波の振動数は何Hzか。
(3)この波の周期は何sか。

まとめ

波の基本的な用語と式について説明をしました。
周期T［s］は1回振動するのにかかる時間、振動数f［Hz］は1秒間に振動する回数であり、

$$f=\frac{1}{T}$$

という関係があります。

波の基本式

$$v=fλ$$

$$v=\frac{λ}{T}$$

は波動の分野で一番よく使う式なので、勉強しているうちに勝手に覚えてると思います。

 

次の内容はこちら

一覧に戻る