抵抗の繋ぎ方には直列接続と並列接続の2種類があります。
この2つの違いについて理解していない場合は問題が難しく感じるのですが、2つの違いを理解している場合は問題が簡単に解けるようになるため、確実に知っておいた方が良いです。
合成抵抗については、あまり知らなくても大丈夫かもしれません。
今回は、直列と並列の違いと合成抵抗について、わかりやすく簡単に解説をしていきます。
直列とは
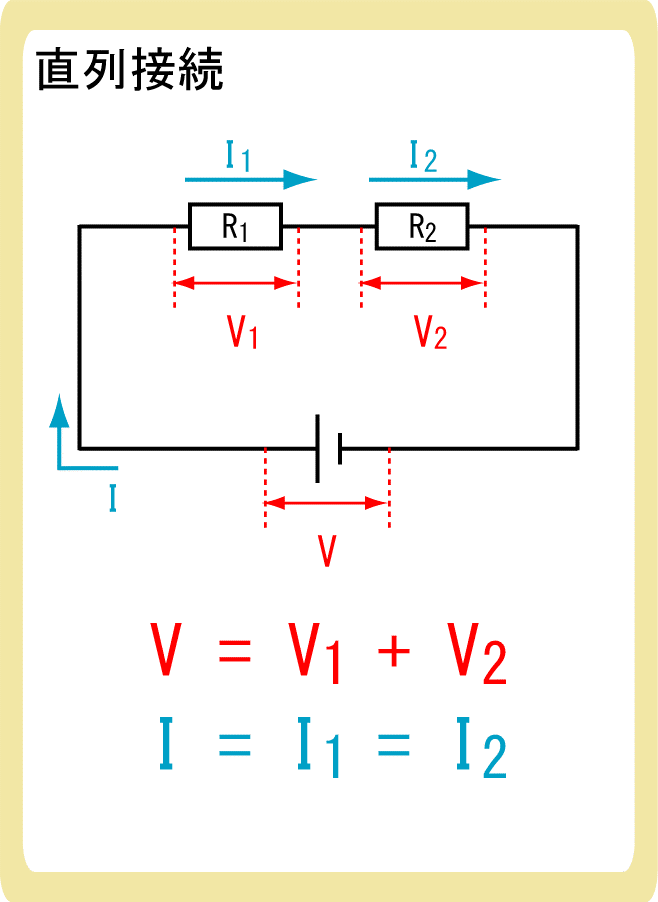
直列接続
各抵抗に加える電圧の和が、全体の電圧と等しい
$$V=V_1+V_2+…$$
各抵抗に流れる電流は等しい
$$I=I_1=I_2=…$$
直列接続とは、複数の抵抗をまっすぐ繋げる方法のことです。
各抵抗に加わる電圧の和は全体の電圧と等しく、各抵抗に流れる電流は等しいという特徴があります。

電流は電気の流れなので、分かれ道がなければ常に同じ強さになります。
つまり、直列接続では電流の強さは常に等しいです。
$$I=I_1=I_2=…$$
詳しくは物理の方で扱うのですが、回路を一周したときの合計の電圧と電池の電圧は等しいので、上図でいうとV1とV2の合計が電池のVと等しくなります。
$$V=V_1+V_2+…$$
並列とは
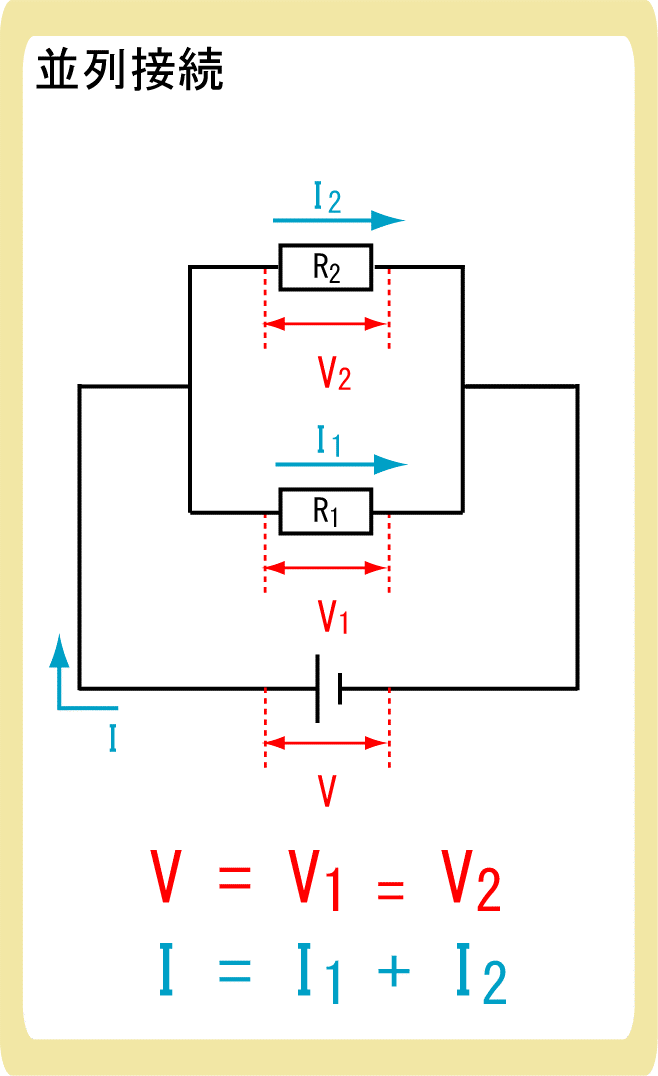
並列接続
各抵抗に加わる電圧は、全体の電圧と等しい
$$V=V_1=V_2=…$$
各抵抗に流れる電流の合計が、全体の電流の合計となる
$$I+I_1+I_2=…$$
並列接続とは、導線やコードが途中で分かれるように抵抗を繋ぐ方法のことです。
各抵抗に加わる電圧は全体の電圧と等しくなり、各抵抗に流れる電流の合計が全体の電流となります。

電流は電気の流れなので、分かれ道があると電流も分かれます。
並列接続では、電流の強さは全体よりも小さくなるのです。
$$I=I_1+I_2+…$$
直列接続と同様に、回路を一周したときの合計の電圧と電池の電圧は等しいので、分かれ道の上側を使って一周しても、分かれ道の下側を使って一周しても、電池の電圧と等しくなります。
つまり、R1とR2に加わる電圧は等しいです。
$$V=V_1=V_2=…$$
これらは、中学2年の理科でも習う内容です。
合成抵抗とは
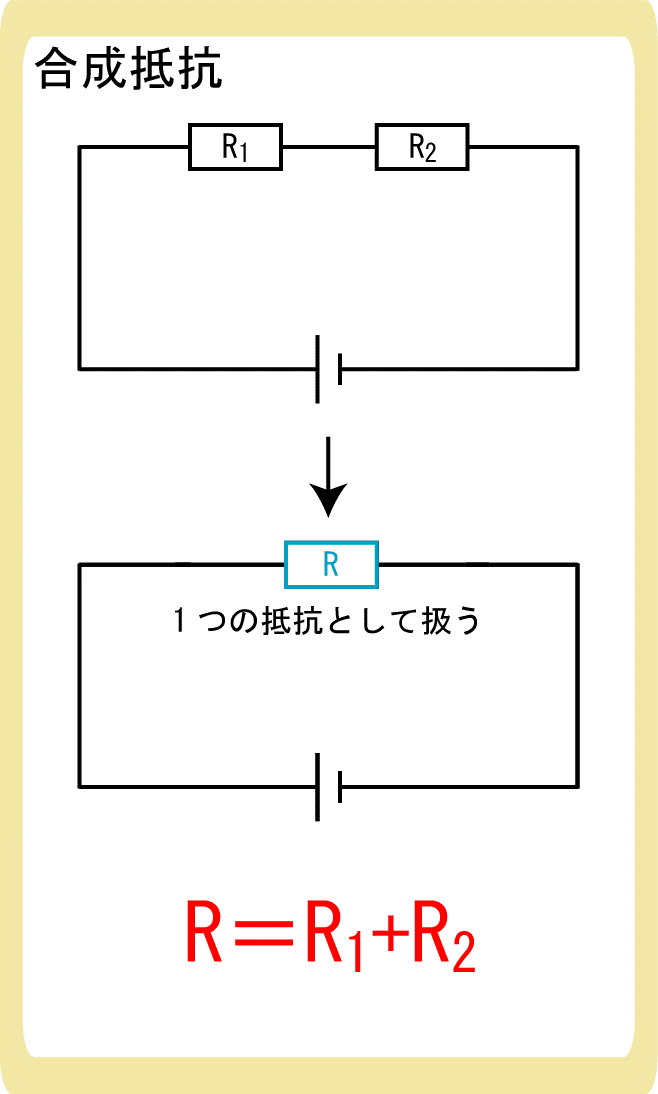
合成抵抗
複数の抵抗を1つの抵抗として扱うこと
直列
$$R=R_1+R_2+…$$
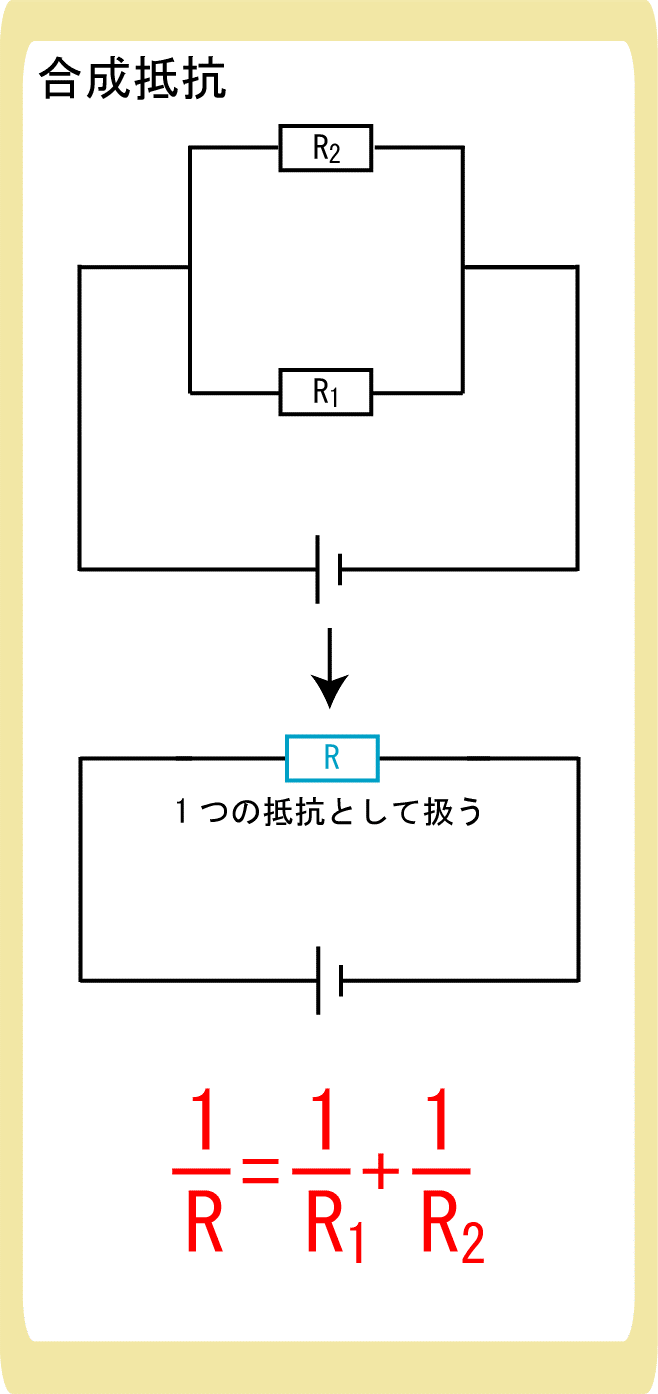
並列
$$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+…$$
合成抵抗とは、複数の抵抗を1つの抵抗として扱うことをいいます。
抵抗が2つ以上ある場合、複数の抵抗を合成して考えることができます。
正直、合成抵抗なんか使わなくても問題を解くことはできるのですが、合成抵抗を使って問題を解くこともできるため、知って損はない内容であると思います。

抵抗の値は、抵抗が長ければ長いほど大きくなります。
2つの抵抗を直列に繋ぐと、その分抵抗が長くなったと考えられるため、抵抗の値は大きくなり、
$$R=R_1+R_2+…$$
という式で表されます。
導出
抵抗R1にかかる電圧をV1、抵抗R2にかかる電圧をV2とします。
直列では電流の強さIは同じになるため、各抵抗にかかる電圧はオームの法則より
$$V_1=R_1×I\\
V_2=R_2×I$$
となります。
全体の電圧をV、合成抵抗をRとしたとき、
$$V=R×I$$
であり、直列なので\(V=V_1+V_2\)ということは、
$$R×I=R_1×I+R_2×I$$
となり、\(R=R_1+R_2\)となります。

抵抗の値は、抵抗が太ければ太いほど(断面積が大きいほど)小さくなります。
抵抗を並列に繋げることは、抵抗が太くなったと考えられるため、抵抗の値は小さくなり、
$$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+…$$
という式で表されます。
導出
抵抗R1に流れる電流をI1、抵抗R2に流れる電流をI 2とします。
並列では電圧Vは同じになるため、各抵抗に流れる電流はオームの法則より
$$I_1=\frac{V}{R_1}\\
I_2=\frac{V}{R_2}$$
となります。
全体の電流をI、合成抵抗をRとしたとき、
$$I=\frac{V}{R}$$
であり、並列なので\(I=I_1+I_2\)ということは、
$$\frac{V}{R}=\frac{V}{R_1}+\frac{V}{R_2}$$
となり、
$$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$$
となります。
合成抵抗についても、中学2年生の理科で習う内容なのですが、物理基礎でも改めて勉強をします。
これらの知識とオームの法則を用いて例題を解いていきましょう。
例題
例題1
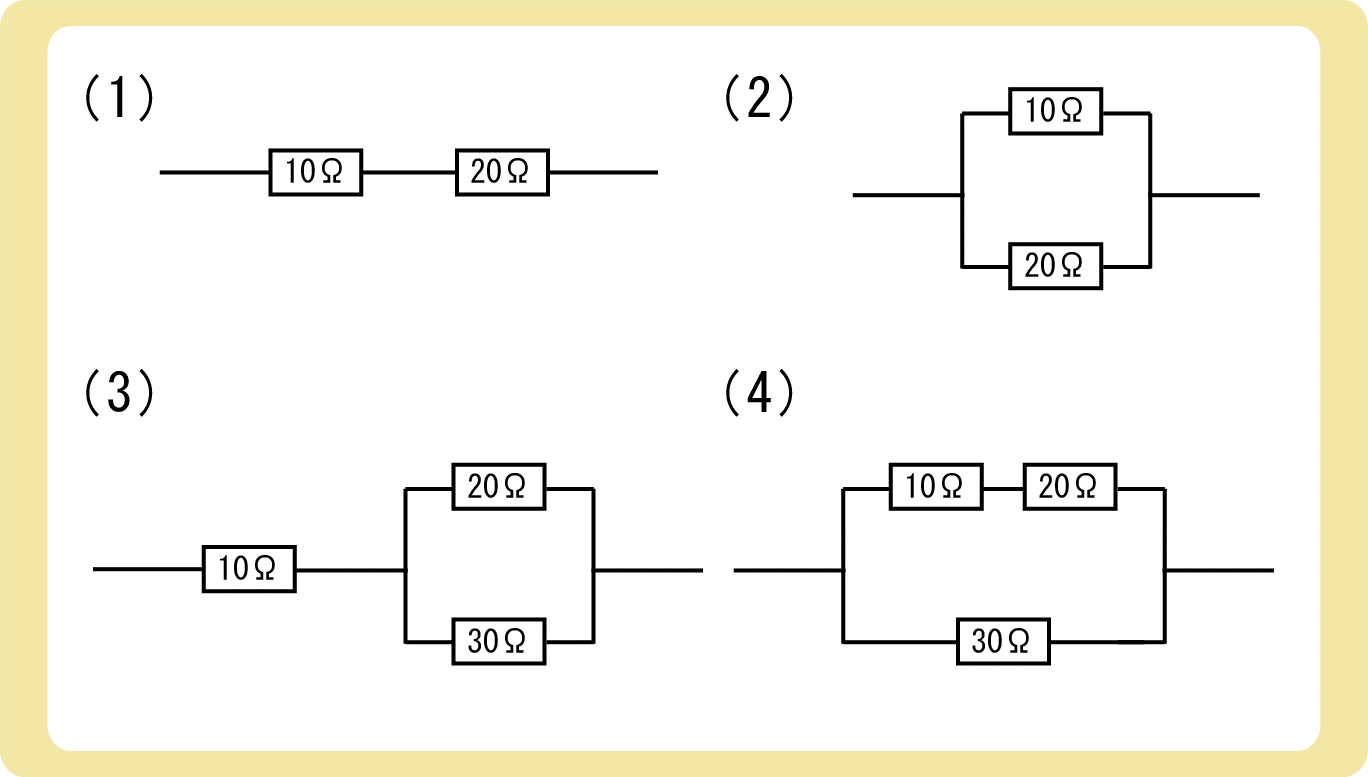
下図のように抵抗が接続されているとき、合成抵抗は何Ωになるか。

解答
直列の場合は
$$R=R_1+R_2+…$$
を使い、並列の場合は
$$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+…$$
を使います。
直列と並列が組み合わさったときは、片方ずつ合成していきます。
(1)直列なので、
$$R=R_1+R_2\\
R=10+20\\
R=30$$
∴30Ω
(2)並列なので、
$$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\\
\frac{1}{R}=\frac{1}{10}+\frac{1}{20}$$
\frac{1}{R}=\frac{3}{20}\\
R=\frac{20}{3}$$
∴\(\frac{20}{3}\)Ω
(3)先に右側の並列を合成し、その後、直列の合成をします。
右側の2つの抵抗を合成することで、(1)のような形になり、直列の合成をすることができるようになります。
10Ωの抵抗をR1、20Ωの抵抗をR2、30Ωの抵抗をR3とすると、右側の抵抗は
$$\frac{1}{R_{23}}=\frac{1}{R_2}+\frac{1}{R_3}\\
\frac{1}{R_{23}}=\frac{1}{20}+\frac{1}{30}$$
\frac{1}{R_{23}}=\frac{5}{60}\\
R_{23}=14$$
となり、あとは直列に合成するので、
$$R=R_1+R_{23}\\
R=10+14\\
R=24$$
となります。
∴24Ω
(4)先に上側の2つの抵抗を直列に合成し、(2)のような形にした後に並列の合成をします。
10Ωの抵抗をR1、20Ωの抵抗をR2、30Ωの抵抗をR3とすると、上側の抵抗R12は30Ωになるので、
$$\frac{1}{R}=\frac{1}{R_{12}}+\frac{1}{R_3}\\
\frac{1}{R}=\frac{1}{30}+\frac{1}{30}$$
\frac{1}{R}=\frac{2}{30}\\
R=15$$
∴15Ω
例題2
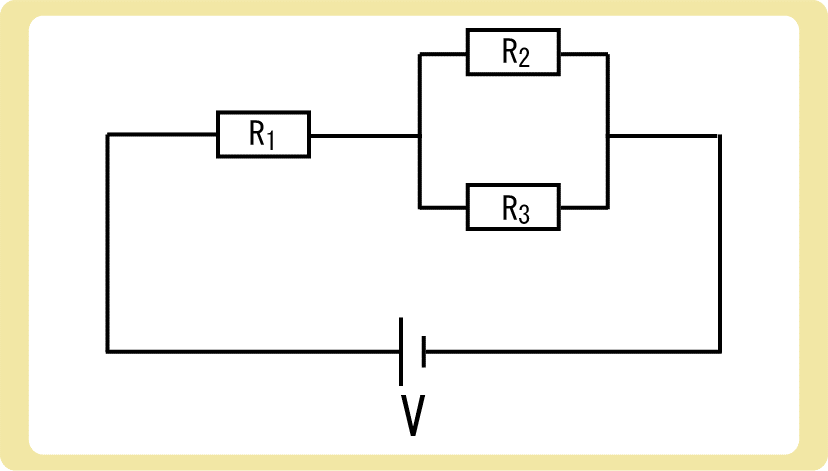
下図のような回路があり、抵抗R1、R2、R3の値がそれぞれ2Ω、4Ω、6Ωであり、電源の電圧が22Vのとき、以下の各問に答えなさい。
(1)抵抗R1に流れる電流は何Aか。
(2)抵抗R2にかかる電圧は何Vか。
(3)抵抗R3に流れる電流は何Aか。

解答
直列と並列の違いと特徴、合成抵抗、オームの法則を駆使して問題を解きます。
ポイントは
・全体に流れる電流とR1に流れる電流は等しい。(R1には分かれ道がないから)
・オームの法則で使うVは22Vとは限らない。どの抵抗かによってVは異なる。
・1周で22Vなので、R1が何Vか分かればR2とR3のVも分かる。
です。
(1)まずは合成抵抗を求め、全体に流れる電流を求めましょう。
R2とR3は並列なので、
$$\frac{1}{R_{23}}=\frac{1}{R_2}+\frac{1}{R_3}\\
\frac{1}{R_{23}}=\frac{1}{4}+\frac{1}{6}\\
\frac{1}{R_{23}}=\frac{5}{12}\\
R_{23}=2.4$$
次に、R1とR23を直列として合成すると、
$$R=R_1+R_{23}\\
R=2+2.4\\
R=4.4$$
全体の抵抗は4.4Ωとなります。
次に、オームの法則を使い、全体の抵抗と全体の電圧から、全体の電流を求めます。
$$V=RI\\
22=4.4×I\\
I=5$$
全体に流れる電流は5Aであり、R1に流れる電流は全体の電流と等しいため、抵抗R1に流れる電流も5Aになります。
∴5A
(2) (1)でR1に流れる電流が求まったため、オームの法則を使いR1の電圧を求めることができます。
R1の電圧を求めるためには、R1の抵抗値とR1に流れる電流の強さをオームの法則に代入しましょう。
$$V=RI\\
V_1=R_1×I_1\\
V_1=2×5\\
V_1=10$$
R1にかかる電圧が10Vということは、R2とR3にかかる電圧は12Vであると分かります。
この回路は1周で22Vなので、R1が10Vということは、上のR2を通っても下のR3を通っても残りの12Vということになります。
∴12V
(3)全体の電流は5Aですが、R2とR3は2つに分かれているので、電流も2つに分かれてしまいます。
しかし、R3の抵抗値とR3の電圧が分かっているので、オームの法則を使ってR3の電流を求めることができます。
$$V=RI\\
V_3=R_3×I_3\\
12=6×I_3\\
I_3=2$$
∴2A
R2とR3の抵抗値は4Ωと6Ωです。
4Ωと6Ωは2:3であり、電流も2:3で分かれるため、R3に流れる電流は2Aであると分かります。
(R3の方が抵抗値は大きいため、R3の方が電流は流れにくい。)
まとめ
電圧は1周で電池と同じ値ことと、電流は分かれ道で分かれることから、直列では各抵抗の電圧の和が電源の電圧になり、並列では各抵抗の電流の和が全体の電流になります。
また、複数の抵抗がある場合、合成抵抗を考えることによって問題を解くことがあります。
直列では
$$R=R_1+R_2+…$$
並列では
$$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+…$$
という式で表されるということを、なんとなく知っておきましょう。
次の内容はこちら
一覧に戻る