・屈折とは
・どっちに屈折するのか
・屈折の法則とは
今回は、波の屈折と屈折の法則について、わかりやすく簡単に解説していきます。
屈折とは
境界面で波の進む向きが変わること
屈折とは、境界面で波の進む向きが変わることです。

水族館でイルカ等を見るときや、上の写真など、屈折という現象は誰しもが知っていると思います。
どっちに屈折するのか
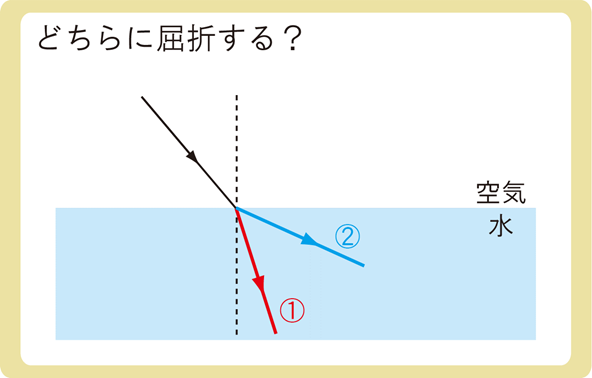
上図のように光が空気中から水に進むとき、①と②のどちらに屈折すると思いますか?
屈折のことは知っていても、どっちに屈折するのかを知っている人は少ないように感じます。
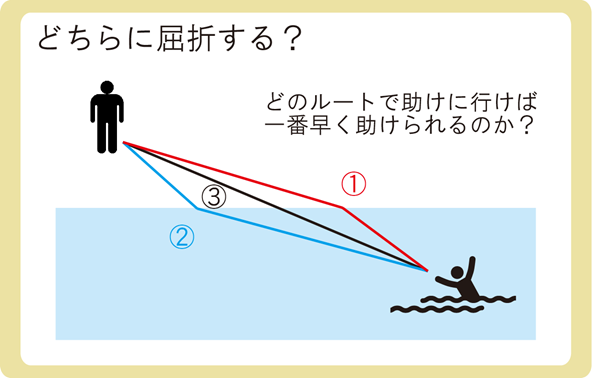
上図のとき、①~③のどのルートで助けに行けば一番早く助けられると思いますか?
この問いの答えが、屈折する方向に対する答えになります。
距離が一番短いのは③ですが、泳ぐよりも走る方が早く動けるため、①の方が早く助けに行くことができるでしょう。
光も空気中よりも水の中の方が遅いため、答えは①です。
これは光に関する原理(フェルマーの原理)ですが、他の波が屈折する方向も同じように考えて大丈夫です。
屈折の法則とは
$$\frac{sini}{sinr}=\frac{v_1}{v_2}=\frac{λ_1}{λ_2}=n_{12}$$
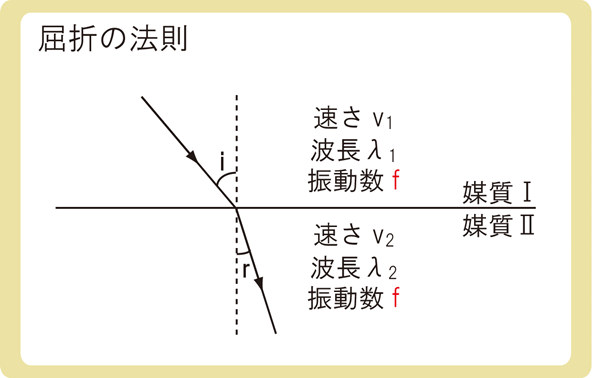
屈折の法則とは、上図のように媒質Ⅰから媒質Ⅱに波が進むとき、\(\frac{sini}{sinr}=\frac{v_1}{v_2}=\frac{λ_1}{λ_2}=n_{12}\)が成り立つことです。
\(n_{12}\)は媒質Ⅰに対する媒質Ⅱの屈折率のことであり、相対屈折率ともいいます。
なお、角度、速さ、波長は変化するのですが、屈折するとき振動数は変化しません。
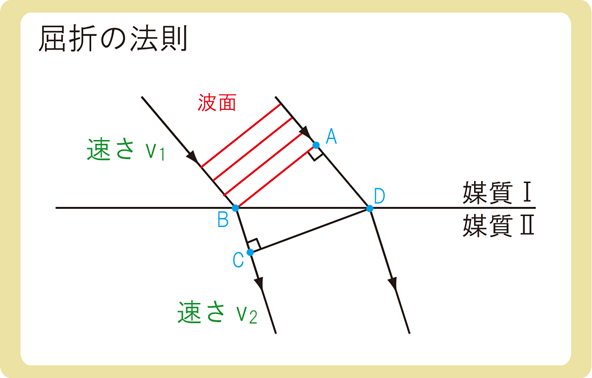
上図のように、平面波が屈折する場合を考えます。
平面波の波面は上図の赤い線であるため、AとBは同時刻、CとDも同時刻です。
(波の左端がBのとき、波の右端はAということです。)
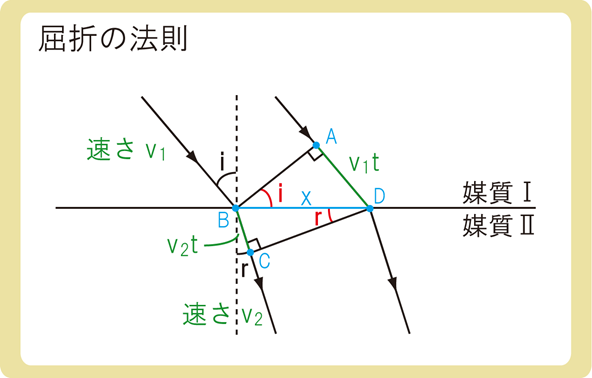
AからDまでの時間とBからCまでの時間は同じなので、tで表します。
媒質Ⅰでの速さは\(v_1\)、媒質Ⅱでの速さは\(v_2\)なので、上図の緑色の線の長さは\(v_1t\)と\(v_2t\)になります。
上図の赤い角度が入射角\(i\)と屈折角\(r\)となるため、BDの長さをxとすると
$$\begin{eqnarray}sini&=&\frac{v_1t}{x}\\
sinr&=&\frac{v_2t}{x}\end{eqnarray}$$
となり、式を整理すると\(\frac{sini}{sinr}=\frac{v_1}{v_2}\)となります。
振動数が変わらないことと、\(v=fλ\)を利用すると、
$$\begin{eqnarray}\frac{v_1}{v_2}&=&\frac{ fλ_1}{fλ_2}\\
&=&\frac{λ_1}{λ_2}\end{eqnarray}$$
となり、屈折の法則が成り立つと考えられます。
例題
例題1
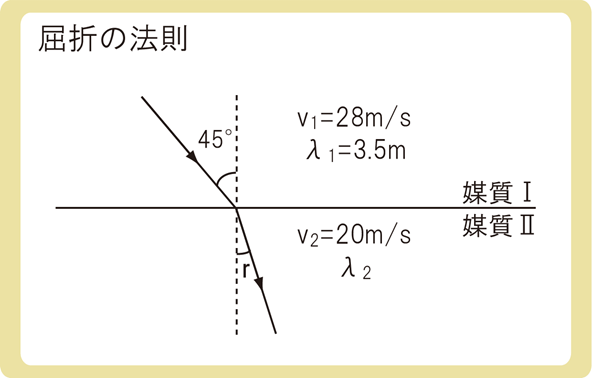
媒質Ⅰでの速さが28m/、波長が3.5mの波が進んでいる。この波が入射角が45°で媒質Ⅱに入射したとき、以下の各問に答えなさい。ただし、\(\sqrt{2}=1.4\)とする。
(1)媒質Ⅱでの波長を求めなさい。
(2)屈折角rを求めなさい。
(3)媒質Ⅰに対する媒質Ⅱの屈折率を求めなさい。
(4)この波の振動数を求めなさい。
まとめ
屈折とは、境界面で波の進む向きが変わることであり\(\frac{sini}{sinr}=\frac{v_1}{v_2}=\frac{λ_1}{λ_2}=n_{12}\)が成り立つことを屈折の法則といいます。
屈折の法則については、光の方がよく登場するため、とりあえず屈折の法則があることだけ知っておきましょう。










