ドップラー効果とは

救急車が近づいたり遠ざかったりすると音の高さが変化する、ということで有名なドップラー効果。

高校物理ではドップラー効果についてどう学ぶのか？

ドップラー効果とは何か？について説明していきます。

ドップラー効果とは

ドップラー効果とは波源や観測者が動くとき観測する振動数が変化する現象のことです。

救急車が通り過ぎるとサイレンの音が急に低くなったように感じますよね。それがドップラー効果です。

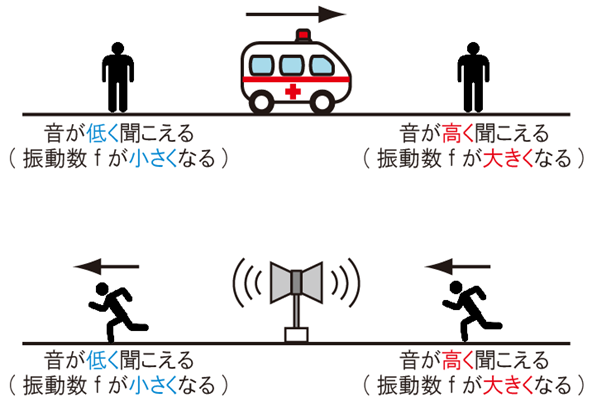
ドップラー効果では、

という特徴があり、音源が動く場合と観測者が動く場合を別々に考えます。

音源が動く場合

音源が動くとλが変化します。

ドップラー効果のシミュレーション このサイトで見るのが分かりやすいですね。

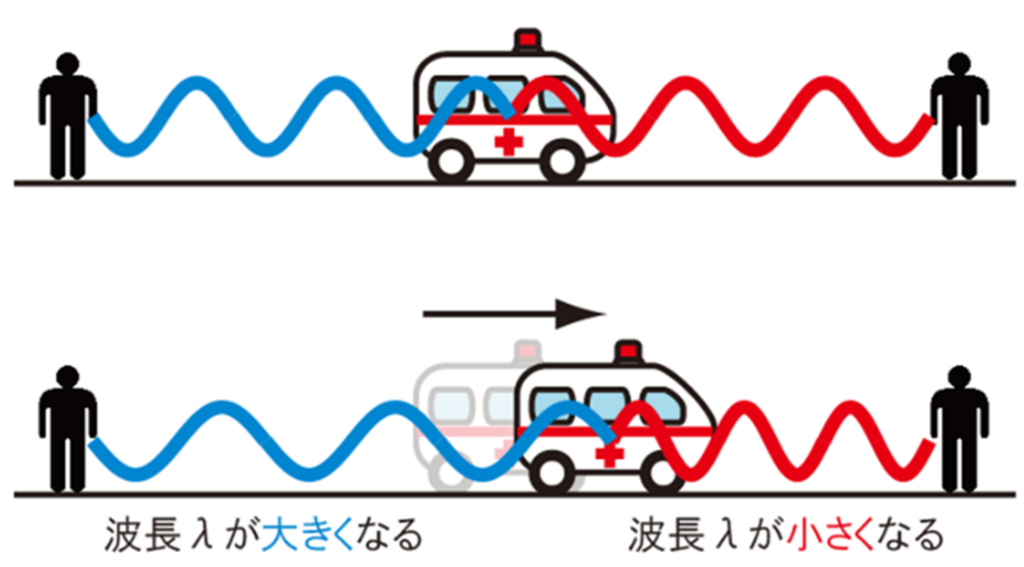
音源が動くと波長が圧縮されたり伸びたりするので、音源の進行方向の前方では波長が小さくなり、後方では波長が大きくなります。

例えば、10mの範囲に波が5個あるとすると、波1個あたり2mの長さなので波長が2mと分かります。

つまり、

$$波長=\frac{個数}{長さ}$$

と表されます。

振動数\(f\)[Hz]は1秒で振動する回数なので、440Hzなら1秒で440個の波が出ることになります。

つまり、\(ft\)が波の個数です。

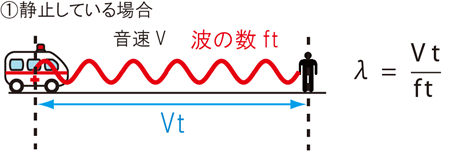
音源が振動数\(f\)の音を連続して出し、初めに出した音が観測者に到達するまでにかかる時間を\(t\)とします。

音源が静止している場合、音源と観測者の間の距離は\(Vt\)になりますよね。

$$波長=\frac{個数}{長さ}$$

ならば、

$$λ=\frac{Vt}{ft}$$

となります。

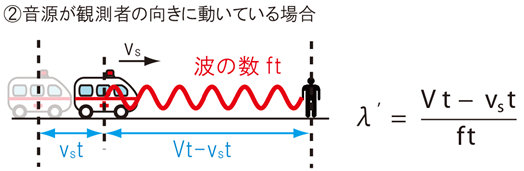
音源の速さをv_s（音速より十分小さい）として、音源が観測者の向きに動いている場合を考えます。

音源が一番左にあるときに音源が最初に音を出したとすると、音の最初の部分は\(t\)秒で観測者までたどり着くので、音の右端は音源が止まってるときと変わりません。

一方、音の左端は音源が進んだ分だけ観測者までの距離も短くなるので、波の数は\(ft\)個で変わらないにもかかわらず、距離が\(Vt―v_st\)に縮んでいると考えられます。

つまり、

$$波長=\frac{個数}{長さ}$$

から、

$$λ’=\frac{Vt-v_st}{ft}$$

となります。

音速は一定なので、λが変化すると振動数\(f\)も変化すると考えます。

$$\begin{eqnarray}V&=&f’λ’\\
V&=&f’×\frac{Vt-v_st}{ft}
\end{eqnarray}$$

この式を整理すると、

$$f’=\frac{V}{V-v_s}f$$

となります。

観測者が動く場合

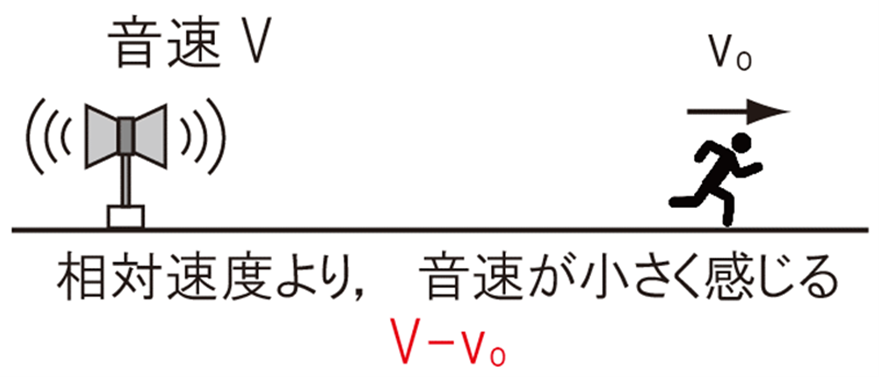
音源が動いていないので波長は変わりませんが、観測者が動くので相対速度より音速が変化しているように感じます。

例えば、上図のように観測者が音源から遠ざかるとき、音速は遅くなったように感じます。

$$V’=V-v_0$$

\(v=fλ\)より、

$$λ=\frac{V}{f}$$

また、\(v=fλ\)より、

$$V’=f’λ$$

に、\(V’\)とλをそれぞれ代入すると、

$$V-v_0=f’×\frac{V}{f}$$

となり、式を整理することで、

$$f’=\frac{V-v_0}{V}f$$

となります。

音源も観測者も動く場合

今の2つの式

$$f’=\frac{V}{V-v_s}f$$

$$f’=\frac{V-v_0}{V}f$$

この二つを組み合わせて、

$$f’=\frac{V-v_0}{V-v_s}f$$

これがドップラー効果の公式になります。

なお、\(v_0\)と\(v_s\)の正負は、音の進む向きが正です。

って、私の高校の頃の物理教師が言っていました。

v_s：波源の速度[m/s]

v₀：観測者の速度[m/s]

です、お忘れなく。