・波の干渉とは
波の干渉は、高校物理の波動において最も重要な内容です。
波の強め合う条件、弱め合う条件を絶対に理解しないといけません。
なお、波の重ね合わせの原理と定常波を理解していないと波の干渉は分からないため、こちらの復習もしておきましょう。
波の干渉とは何かについて、わかりやすく簡単に解説していきます。
波の干渉とは
2つ以上の波が重なり合い、強め合ったり弱め合ったりする現象
2つの波が同位相のとき
|AP-BP|&=&(m+\frac{1}{2})λ・・・弱め合う\end{eqnarray}\\
※m=0, 1, 2, 3…$$
波の干渉とは、2つ以上の波が重なり合い、強め合ったり弱め合ったりする現象のことです。
https://youtu.be/rMsLGSSiSPw?t=245
イメージはこの動画のような感じです。
山と山が重なる点は強め合うため大きく振動し、山と谷が重なる点は弱め合うため振動しません。
なお、谷と谷が重なる点も強め合うと考えます。
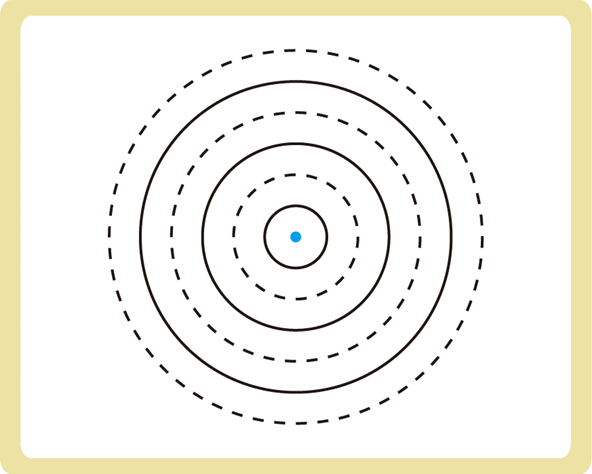
上図のような球面波が2つある場合を考えます。
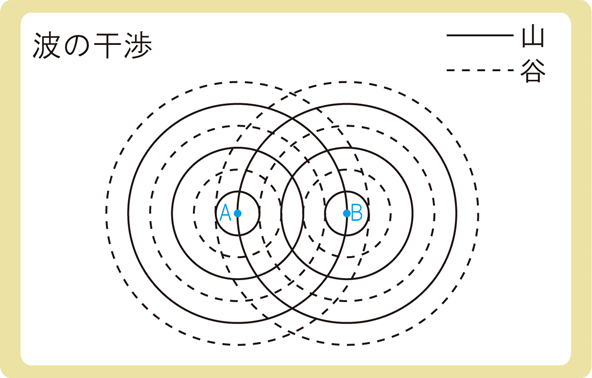
2つの球面波が同位相であるとき、2つの球面波を描くと上図のようになります。
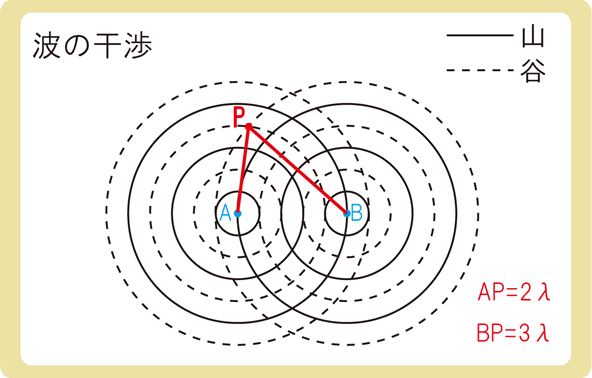
点Pは谷と谷が重なり強め合っている点です。
同位相の2つの球面波では、2つの波源との距離の差がλの整数倍のとき、波は強め合います。
AP=2λ、BP=3λなので、2つの波源との距離の差はλとなり、λの1倍なので強め合うと考えます。
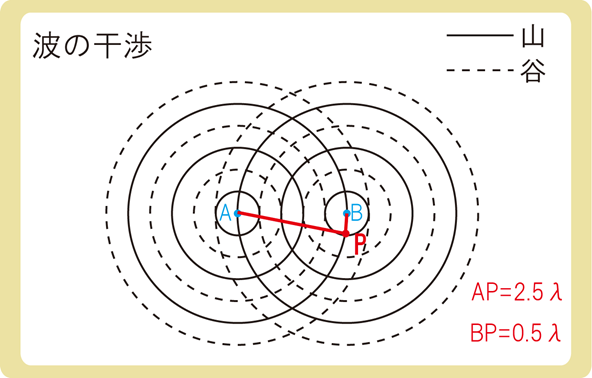
この図では、AP=2.5λ、BP=0.5λなので、2つの波源との距離の差は2λとなり、λの2倍なので強め合います。
山と山が重なっているため、強め合っていることが分かりますね。
これを式にすると、
$$|AP-BP|=mλ・・・強め合う\\
※m=0, 1, 2, 3…$$
となります。
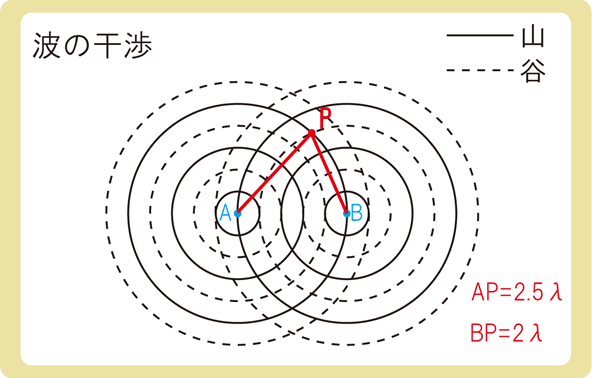
一方、山と谷の重なる点に注目すると、AP=2.5λ、BP=2λなので、2つの波源との距離の差は0.5λです。
同位相の2つの球面波では、2つの波源との距離の差がλの(整数+0.5)倍のとき、波は弱め合います。
これを式にすると、
※m=0, 1, 2, 3…$$
です。
0.5ではなく\(\frac{1}2{}\)と書くことが多いですね。
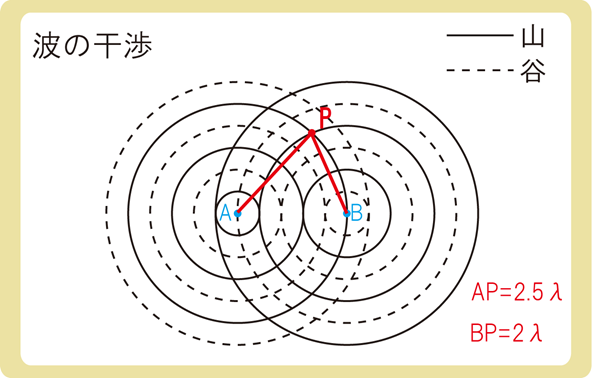
2つの波が逆位相の場合、先程と同じ場所の点Pは山と山が重なる点となり、強め合う点と弱め合うが入れ替わります。
まとめると、
2つの波が同位相のとき
|AP-BP|&=&(m+\frac{1}{2})λ・・・弱め合う\end{eqnarray}\\
※m=0, 1, 2, 3…$$
2つの波が逆位相のとき
|AP-BP|&=&mλ・・・弱め合う\end{eqnarray}\\
※m=0, 1, 2, 3…$$
となります。
例題
例題1
水面上の2点A、Bから波長20cm、振幅10cmの同位相の波が出ている。以下の各問に答えなさい。
(1)点Aから80cm、点Bから60cmの点Pの振動の大きさは何cmか。
(2)点Aから50cm、点Bから40cmの点Qの振動の大きさは何cmか。
例題2
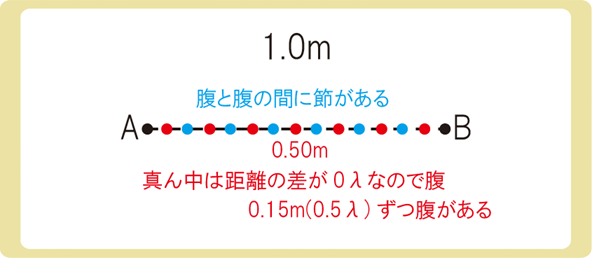
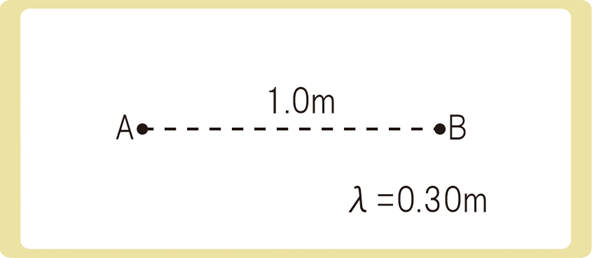
水面上の2点A、Bから波長0.20m、振幅0.10mの同位相の波が出ている。AB間の長さが1.0mのとき、AB間に節はいくつあるか。
まとめ
波の干渉とは、2つ以上の波が重なり合い、強め合ったり弱め合ったりする現象のことで、
2つの波が同位相のとき
|AP-BP|&=&(m+\frac{1}{2})λ・・・弱め合う\end{eqnarray}\\
※m=0, 1, 2, 3…$$
です。
2つの距離の差がλの整数倍かどうかがポイントです。
波の干渉が登場するのは光を考えるときなので、光の干渉でしっかり勉強しましょう。
次の内容はこちら