まず、単原子分子理想気体なので\(ΔU=\frac{3}{2}nRΔT\)を使うことが可能であることを確認しましょう。
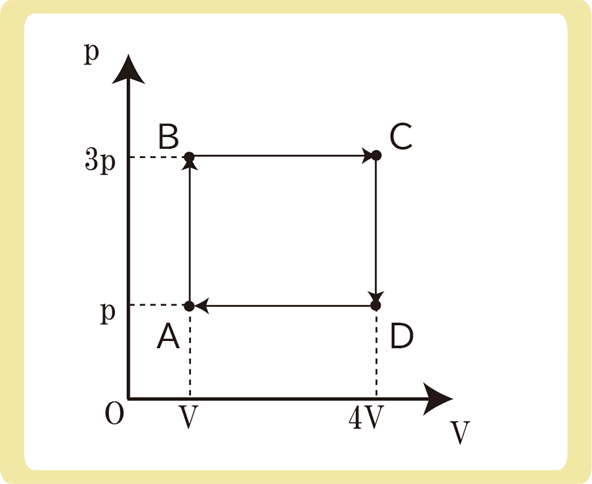
A→Bを①
B→Cを②
C→Dを③
D→Aを④
とします。
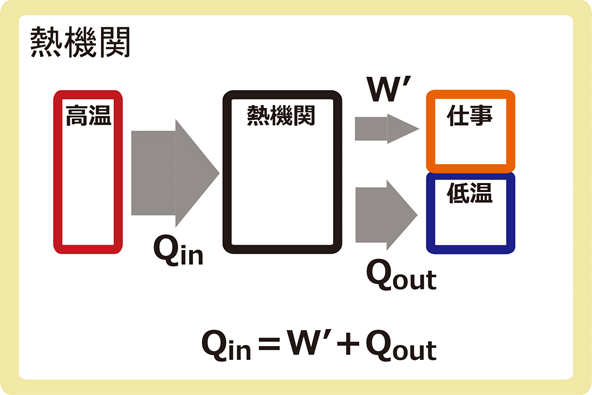
熱効率を求めるためには、①②③④全てのΔU、Qin、Wを求める必要があります。
なお、熱力学第一法則\(ΔU=Q+W\)を用いることで、ΔU、Q、Wのうち2つが分かれば3つ目が分かるので、頑張ってΔU、Q、Wを求めましょう。
p-Vグラフの問題は熱効率に限らずΔU、Q、Wを求めることで問題を解くことができます。
ΔUは、単原子分子理想気体であるため\(ΔU=\frac{3}{2}nRΔT\)を使います。
Qは、定積のときは\(Q=nC_VΔT\)、定圧のときは\(Q=nC_pΔT\)を使います。
また、単原子分子理想のときは、\(C_V=\frac{3}{2}R\)、\(C_p=\frac{5}{2}R\)であることも使います。

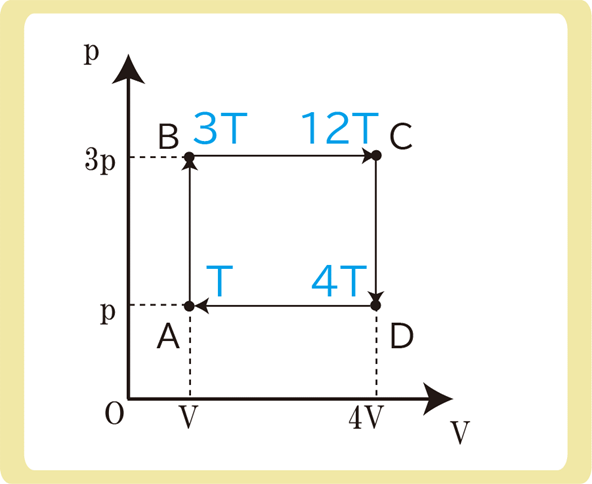
p-Vグラフを見ると、A~Dの絶対温度が一瞬で求めることができます。
A→Bで圧力が3倍なので絶対温度も3倍の3T、
B→Cで体積が4倍なので絶対温度も4倍の12T、
C→Dは圧力が\(\frac{1}{3}\)倍なので絶対温度も\(\frac{1}{3}\)倍の4T、
D→Aは体積が\(\frac{1}{4}\)倍なので絶対温度も\(\frac{1}{4}\)倍のT、
です。
絶対温度が分かるので、ΔTも簡単に求めることが可能ですね。
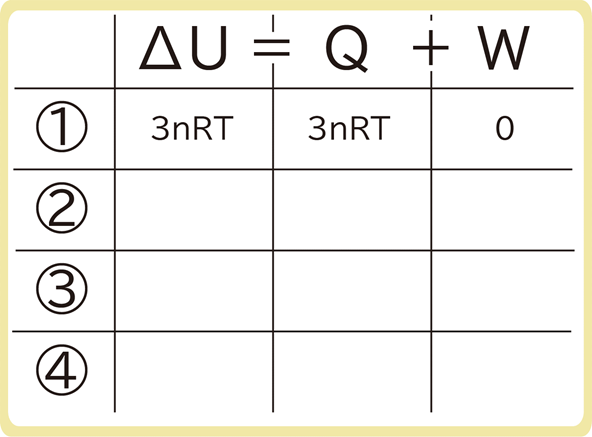
①A→Bは定積変化なので\(W=0\)です。
単原子分子理想で定積変化のとき、\(Q=\frac{3}{2}nRΔT\)より、
$$Q=\frac{3}{2}nRΔT\\
Q_{AB}=\frac{3}{2}nR×2T\\
Q_{AB}=3nRT$$
単原子分子理想のとき、内部エネルギーの変化ΔUは\(ΔU=\frac{3}{2}nRΔT\)であるため、
$$ΔU=\frac{3}{2}nRΔT\\
ΔU_{AB}=\frac{3}{2}nR×2T\\
ΔU_{AB}=3nRT$$
となります。

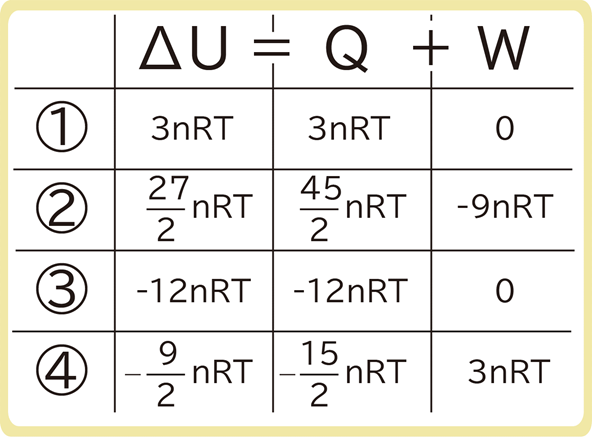
各変化における、ΔU、Q、Wを分かりやすくするため、上のような表を書きましょう。
この問題では、熱力学第一法則\(ΔU=Q+W\)があるので、ΔU、Q、W の3つうちどれか1つの公式を忘れてしまっても問題を解くことが可能です。
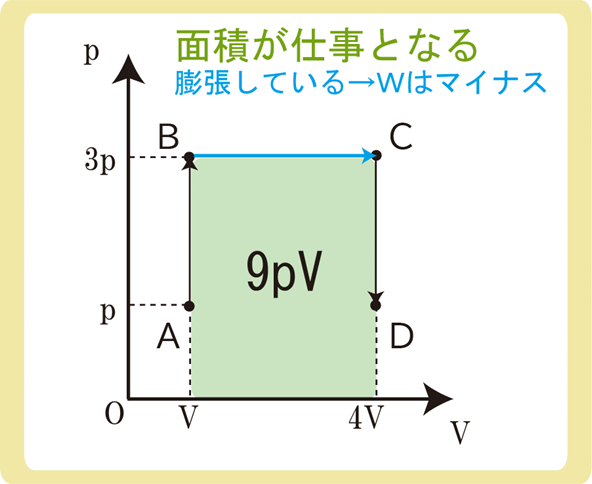
②B→Cは定圧変化であるため、\(W=-pΔV\)です。
$$W=-pΔV\\
W_{BC}=-3p×(4V-V)\\
W_{BC}=-9pV\\
W_{BC}=-9nRT$$

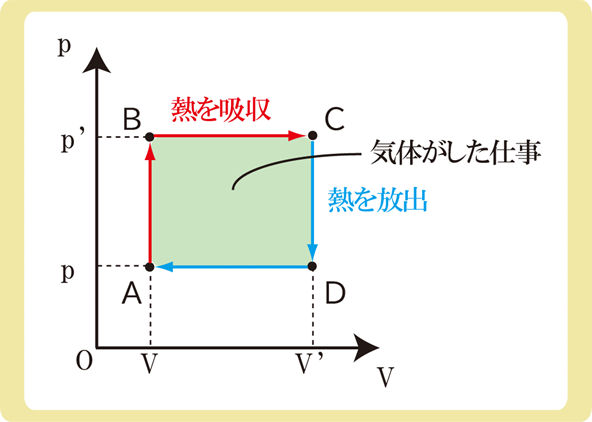
上図の面積が仕事になるため、\(W=-pΔV\)を覚えていなくても仕事の大きさが9pVであると求めることができます。
なお、気体が膨張しているときは気体が仕事をしているため、Wはマイナスになります。
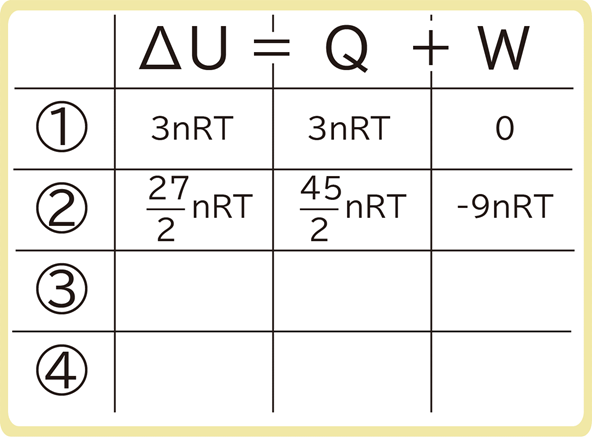
単原子分子理想で定圧変化のとき、\(Q=\frac{5}{2}nRΔT\)より、
$$Q=\frac{5}{2}nRΔT\\
Q_{BC}=\frac{5}{2}nR×9T\\
Q_{BC}=\frac{45}{2}nR $$
単原子分子理想のとき、内部エネルギーの変化ΔUは\(ΔU=\frac{3}{2}nRΔT\)であるため、
$$ΔU=\frac{3}{2}nRΔT\\
ΔU_{BC}=\frac{3}{2}nR×9T\\
ΔU_{BC}=\frac{27}{2}nRT$$
となります。

③と④も同様に考えます。
①C→Dは定積変化なので\(W=0\)です。
単原子分子理想で定積変化のとき、\(Q=\frac{3}{2}nRΔT\)より、
$$Q=\frac{3}{2}nRΔT\\
Q_{CD}=\frac{3}{2}nR×(-8T)\\
Q_{CD}=-12nRT$$
単原子分子理想のとき、内部エネルギーの変化ΔUは\(ΔU=\frac{3}{2}nRΔT\)であるため、
$$ΔU=\frac{3}{2}nRΔT\\
ΔU_{CD}=\frac{3}{2}nR×(-8T)\\
ΔU_{CD}=-12nRT$$
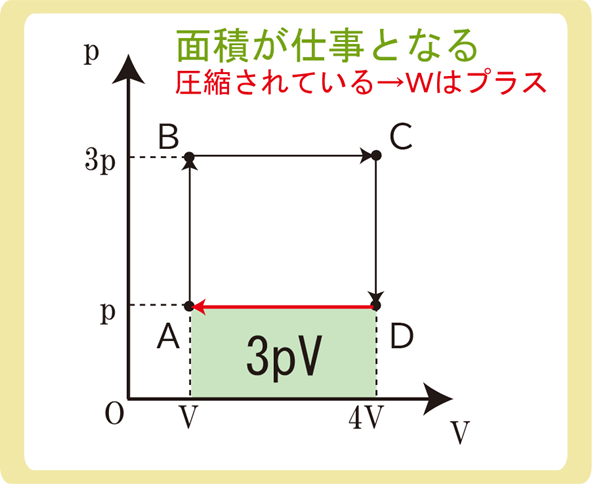
④D→Aは定圧変化であるため、\(W=-pΔV\)です。
$$W=-pΔV\\
W_{DA}=-p×(V-4V)\\
W_{DA}=3pV\\
W_{DA}=3nRT$$

上図の面積が仕事になるため、\(W=-pΔV\)を覚えていなくても仕事の大きさが3pVと分かります。
単原子分子理想で定圧変化のとき、\(Q=\frac{5}{2}nRΔT\)より、
$$Q=\frac{5}{2}nRΔT\\
Q_{DA}=\frac{5}{2}nR×(-3T)\\
Q_{DA}=-\frac{15}{2}nR $$
単原子分子理想のとき、内部エネルギーの変化ΔUは\(ΔU=\frac{3}{2}nRΔT\)であるため、
$$ΔU=\frac{3}{2}nRΔT\\
ΔU_{DA}=\frac{3}{2}nR×(-3T)\\
ΔU_{DA}=-\frac{9}{2}nRT$$
となります。

上図より、吸収した熱量は\(Q_{in}=3nRT+\frac{45}{2}nRT \)であり、1周で気体がした仕事は\(W’=-(-9nRT+3nRT)\)、つまり\(W’=6nRT\)となります。
気体がした仕事W’であるため、された仕事Wに-1を掛けるのを忘れないようにしましょう。
熱効率は\(e=\frac{W’}{Q_{in}}\)であるため、
$$e=\frac{W’}{Q_{in}}\\
e=\frac{6nRT}{3nRT+\frac{45}{2}nRT}\\
e=\frac{4}{17}$$
∴\(\frac{4}{17}\)