・正弦波の式とは
・正弦波の式と波の重ね合わせの原理・定常波
波とは何か、正弦波とは何か、については物理基礎の内容を確認してください。
波長λ、振幅A、振動数f、周期Tあたりが分かっていれば、最低限大丈夫でしょう。
今回は、正弦波の式とは何かについてわかりやすく簡単に解説していきます。
正弦波の式とは
$$y=Asin2π(\frac{t}{T}-\frac{x}{λ})$$
正弦波の式とは、\(y=Asin2π(\frac{t}{T}-\frac{x}{λ})\)のことで、波を表す式のことです。

「海の波の高さはどれくらいか?」
と聞かれても、「どこの海なのか」「今日なのか明日なのか」によって波の高さは変わりますよね。
つまり、直線上を進む波の変位yは位置xと時間tによる2変数関数で表されます。物理基礎でもy-xグラフとy-tグラフの違いを勉強したように、波を表すためにはxとtの両方が必要なのです。
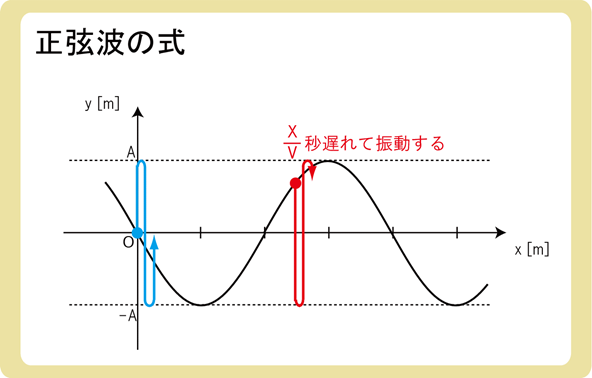
上図のようなx軸正の方向に進む正弦波を考えましょう。
角振動数をωとすると、上図の青い点(x=0)での振動は\(y=Asinωt\)と表すことができます。
波とは”振動が伝わる現象”のことです。
波の速さをvとすると、赤い点は\(\frac{x}{v}\)秒だけ遅れて振動していると考えることができ、\(y=Asinω(t-\frac{x}{v})\)と式で表されます。
円運動でも登場した\(T=\frac{2π}{ω}\)と、\(v=\frac{λ}{T}\)を使うことで、
$$\begin{eqnarray}y&=&Asinω(t-\frac{x}{v})\\
&=&Asin\frac{2π}{T}(t-\frac{x}{v})\\
&=&Asin2π(\frac{t}{T}-\frac{x}{vT})\\
&=&Asin2π(\frac{t}{T}-\frac{x}{λ})\end{eqnarray}$$
となり、この式を正弦波の式といいます。
周期Tは時間、波長λは長さなので、\(\frac{t}{T}\)は時間と時間、\(\frac{x}{λ}\)は長さと長さ、と覚えておくと公式を覚えやすいです。
例題 正弦波の式の使い方
例題1
\(y=2.5sin4π(t-0.25x)\)で表される波がある。この波の振幅、波長、周期、振動数、速さを求めなさい。
正弦波の式と波の重ね合わせの原理・定常波
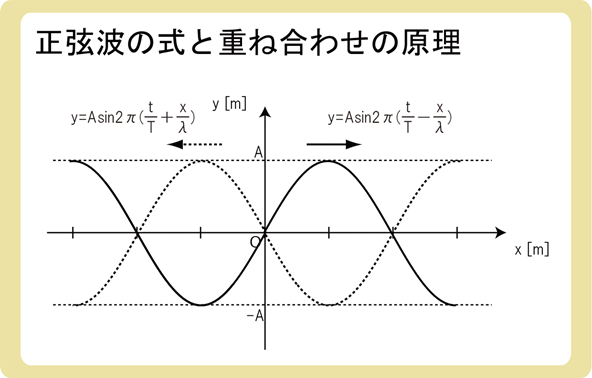
上図のように、\(y=Asin2π(\frac{t}{T}-\frac{x}{λ})\)と\(y=Asin2π(\frac{t}{T}+\frac{x}{λ})\)の2つの正弦波がx軸方向を進んでいるとします。
(なお、x軸方向負の向きに進む場合、正弦波の式は(\(y=Asin2π\frac{t}{T}+\frac{x}{λ})\)となります。)
2つの連続している正弦波が重ね合わさるとき定常波ができるのは物理基礎で勉強しましたね。
重ね合わせの原理より、2つの波から作られる合成波の変位は
で表されます。
数Ⅱで習う三角関数の和積の公式\(sinα+sinβ=2sin\frac{α+β}{2}cos\frac{α-β}{2}\)を使うと
&=&2Asin2π\frac {\frac{t}{T}-\frac{x}{λ}+\frac{t}{T}+\frac{x}{λ}}{2}cos2π\frac{\frac{t}{T}-\frac{x}{λ}-(\frac{t}{T}+\frac{x}{λ})}{2}\\
&=&2Asin2π\frac{t}{T}cos2π(-\frac{x}{λ})\\
&=&2Asin2π\frac{t}{T}cos2π\frac{x}{λ}\end{eqnarray}$$
となります。
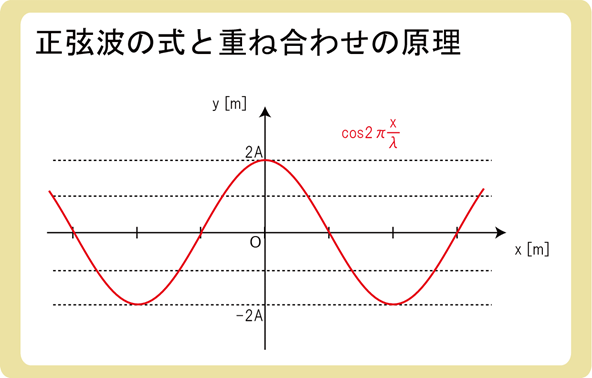
\(y=2Acos2π\frac{x}{λ}\)のみを図にしてみましょう。
この式の変数はxのみであるため、時間が経っても左右に動くことができません。
この式に\(sin2π\frac{t}{T}\)を掛けたのが\(y=2Asin2π\frac{t}{T}cos2π\frac{x}{λ}\)です。
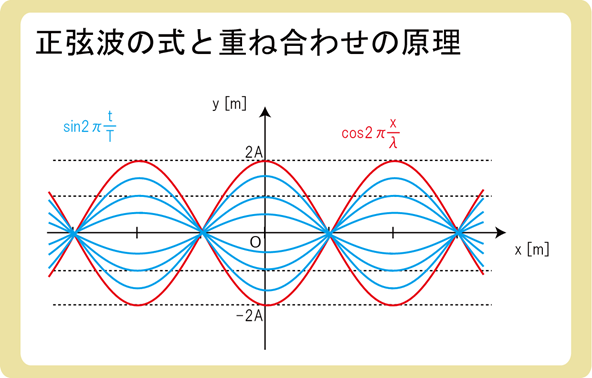
\(sin2π\frac{t}{T}\)は時間tが変わることで、sinの値が-1~1に変化します。
つまり、先程のcosの波の大きさが時間によって変化するということになり、定常波の式となります。
このように、正弦波の式として波をsinで表すことで、重ね合わせの原理から定常波を求めることが可能になります。
まとめ
波の変位は「位置x」と「時間t」によって変化するため、正弦波は\(y=Asin2π(\frac{t}{T}-\frac{x}{λ})\)と表すことができます。
この式を使うことはあまりないかもしれませんが、重ね合わせの原理を使って定常波の式を表すこともできます。










