有効数字とは

物理基礎を習う前に、まずは有効数字についての考え方について解説をします。

物理基礎や物理の教科書や問題集では、何も言及せずにこの記事で説明するようなルールに従って有効数字を定めています。

「あれ？19.6って計算で出たのに、答えが20になっている…」

ということが多々あります。

しかし、高校物理で扱っている有効数字の考え方は、厳密なものではありません。

あくまでも便宜上そう扱っているだけなので、とりあえず高校物理ではこういうルールで計算しているのだなと思って大丈夫です。

学校によっては有効数字を気にせず無視をしていいと教えてもらっているところもあるかもしれませんね。

それでは、有効数字をわかりやすく簡単に解説していきます。

有効数字とは

有効数字とは「数字の正確さを表す方法」のことです。
5.8と5.80を同じ意味だと思ってしまいますが、測定した値として考えると意味が異なってきます。

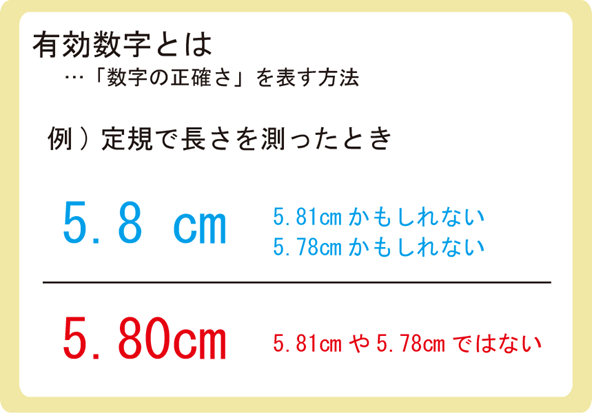
例えば、定規で測ったとき、長さが5.8cmであったとします。
この5.8cmは5.81cmかもしれないですし、5.79cmかもしれません。
定規で測ったため、ぴったり5.8000000…cmではなく誤差が生じてしまいます。

もし、より細かく長さを測れる定規を使って5.80cmと測定した場合、少なくとも5.81cmや5.79cmではなかったということが分かります。(5.801cmかもしれませんが…)

このような、数値がどこまで細かく分かっているのかを表したものを有効数字といいます。

有効数字の桁数の数え方

具体的に有効数字をどう扱っているのかについて解説をします。

有効数字の桁数の数え方はとても単純で、0ではない数字より前にある0を数えず、0ではない数字が来てから何桁かを数えればよいです。
文章で読むと意味が分からないので、図で確認しましょう。

末尾にある0は数えてよく、10.0000ならば有効数字の桁数は6桁となります。

1.0    2桁
0.10   2桁
0.010  2桁
10.0   3桁

このように、左から何桁あるかを数えることになっています。

有効数字の指数表示

高校物理では、有効数字の桁数が何桁なのかを分かりやすくするため、指数を用いて有効数字を表します。

大きい数字や小さい数字は1桁目と2桁目の間に小数点が来るように表示します。ただし、有効数字の桁数は変えません。

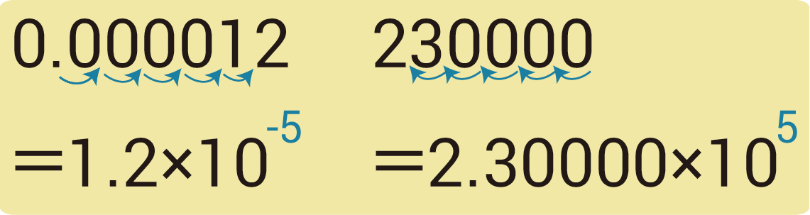
単純に、0の数が指数の数であると考えても大丈夫です。

$$0.000012 ＝ 1.2×10^{-5}\\
230000 ＝ 2.30000×10^5$$

桁数が少ないのであれば指数表示をしなくて分かりやすいのですが、物理では10桁や20桁の数字が当たり前のように現れてくるので指数表示をしないと分かりにくくなってしまいます。

特に、物理基礎でも電気の分野になると桁数が大きく(小さく)なるため、早いうちに慣れておくと良いでしょう。

指数計算

物理基礎では指数表示をするため、指数の状態のまま計算をすることが多いです。

指数同士の計算をする方法は、掛け算のときは指数を足し、割り算のときは指数を引けば大丈夫です。

$$2^2×2^3=4×8=32=2^5=2^{2+3}\\
2^2×2^3＝2^{2+3}$$

$$2^5÷2^2＝32÷4＝8＝2^3＝2^{5-2}\\
2^5÷2^2＝2^{5-2}$$

となります。
これは指数がマイナスのときでも同じように計算をします。

例えば

$$5^{-10}×5^3＝5^{-7}$$

$$5^3÷5^{-10}＝5^{13}$$

となります。

ただし、5²×3⁶のように指数の底が揃っていないときは計算ができないため注意しましょう。

有効数字の計算

有効数字の計算は

（1）足し算・引き算
（2）掛け算・割り算
（3）定数を含む計算

で、それぞれ扱い方が異なります。

（1）足し算・引き算

（1）足し算・引き算では、計算結果の末位を最も高いものに合わせます。

（2）掛け算・割り算

（2）掛け算・割り算では、計算結果の桁数を有効数字の桁数が最も少ないものに合わせます。

（3）定数を含む計算

（3）定数を含む計算では、定数を他の値よりも1桁多く取り出して計算します。

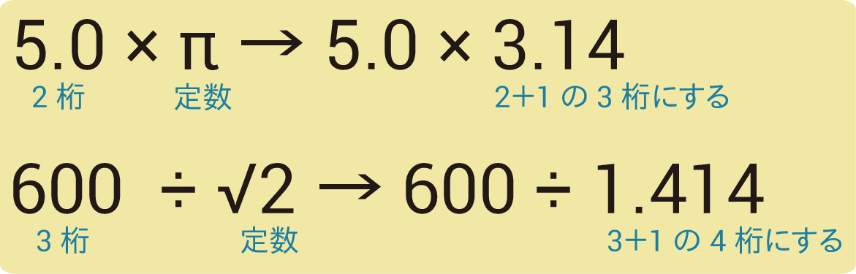
模範解答を見たとき、どうして有効数字がそうなったのか分からなかった場合、この3つのルールを確認すると計算方法に納得できると思います。

三角比とは

おまけに三角比について簡単にお話しします。

物理では三角比をよく使うので、どれがsinなのかcosなのかを必ず覚えておきましょう。

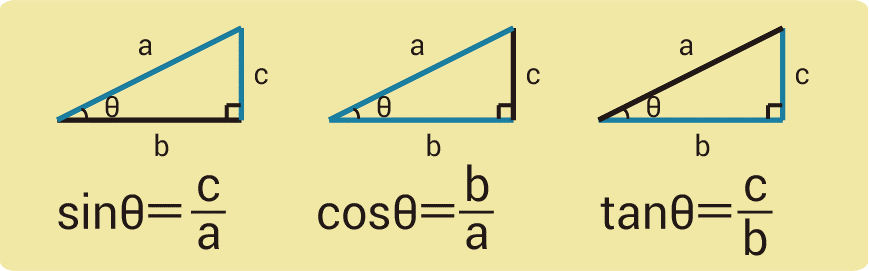
三角比は数学1の後半に習う内容であるため、高校一年生で物理基礎を習う生徒はsinやcosを使わずに物理基礎を習うかもしれません。

どちらにせよ、θが30°と45°、60°の直角三角形の辺の比は必ず覚えておきましょう。

 

以上で物理の準備は終わりです。

これから物理の勉強を一緒に頑張りましょう！

一覧に戻る