・力のつり合いとは
・3つ以上の力がある場合の力のつり合い
力がないと物体は動き出しません。
しかし、力がないから止まっているとも限りません。
物体が静止しているとき、力のつり合いというものを必ず考えます。
今回は、力のつり合いとは何かについて、わかりやすく簡単に解説します。
力のつり合いとは
物体にはたらいている全ての合力=0 の状態。
右向きの合力=左向きの合力
上向きの合力=下向きの合力
力のつり合いとは、物体にはたらいている全ての合力=0である状態のことです。
力があると物体は動きますが、動かない物体には力がないというわけではありません。
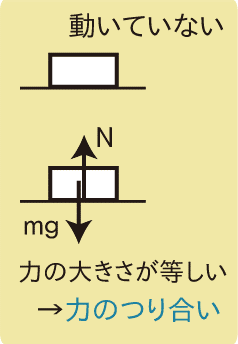
例えば、床に置いてある物体を考えましょう。
この物体には重力mgと垂直抗力Nの2つの力がはたらいています。
このとき、重力mgの大きさと垂直抗力Nの大きさが等しいと物体は静止したままになり、このような状態を力のつり合いといいます。
物体が静止しているときは、物体に力がはたらいていないか、力がつり合っているのかのどちらかなのですが、
物体が静止しているときは、必ず力のつり合いについて考えます!
3力以上のつり合い
力が3つ以上ある場合でも、物体が静止しているときは力のつり合いを考えます。
もし斜めの方向の力があった場合は、上下左右に分解しましょう!
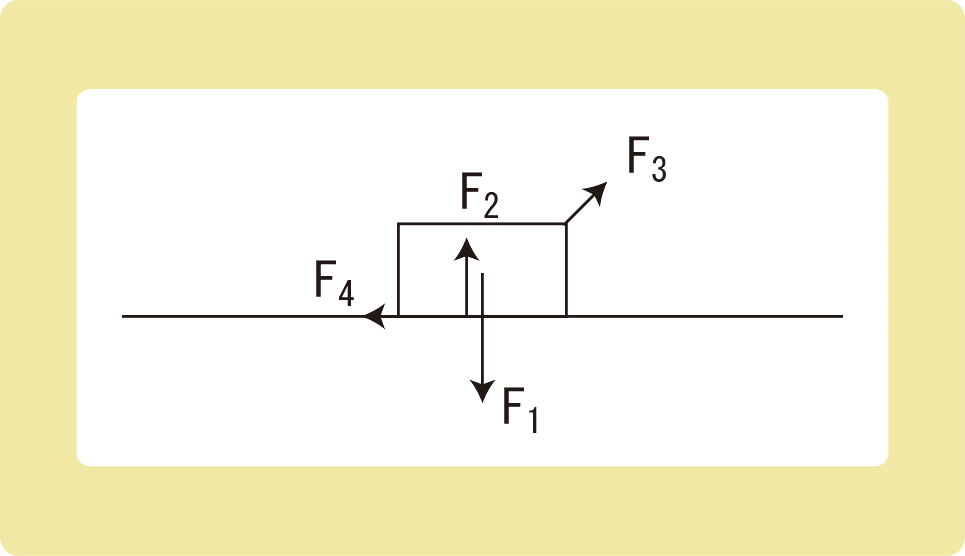
例えば、静止している物体にF1~F4の4つの力がはたらいているとします。
物体が静止しているということは、力がつりあっているということであり、
\begin{cases}
右向きの合力=左向きの合力\\
上向きの合力=下向きの合力
\end{cases}
となっているはずです。
しかし、斜めの力がある場合は、まず斜めの力を分解してから力のつり合いを考えます。
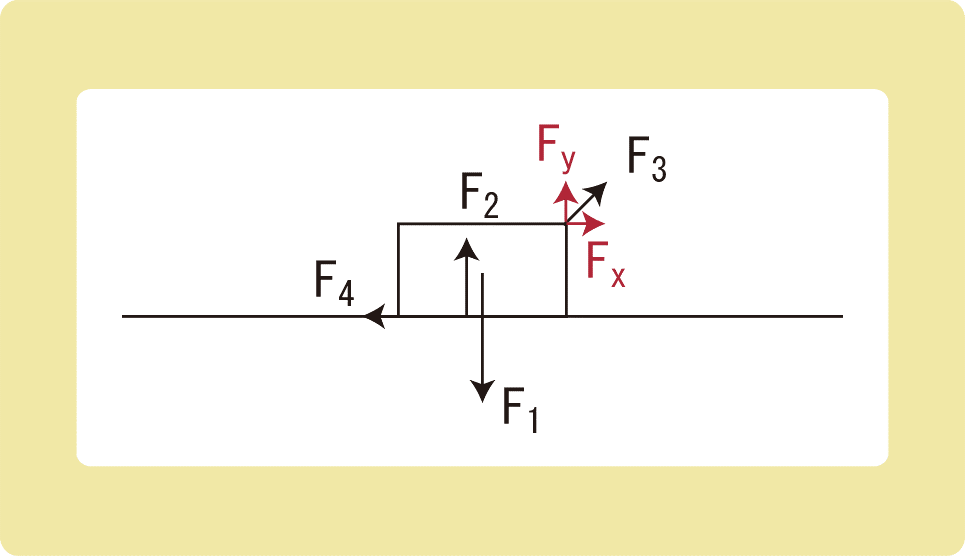
図の赤い矢印のように力を分解し、
\begin{cases}
F_x=F_4\\
F_2+F_y=F_1
\end{cases}
と式を作ります。
このように、物体が静止しているときは必ず力のつり合いの式を立てるようにしましょう。
例題
例題1
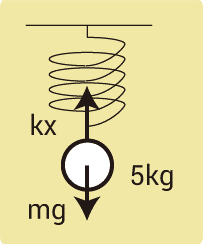
バネでつり下げられ静止している5.0kgの物体について、以下の問に答えよ。ただし、重力加速度の大きさは9.8m/s2とする。
(1)物体にはたらく重力の大きさは何Nか。
(2)物体をつり下げる前と比べてバネは0.10m伸びた。バネ定数は何N/mか。
例題2
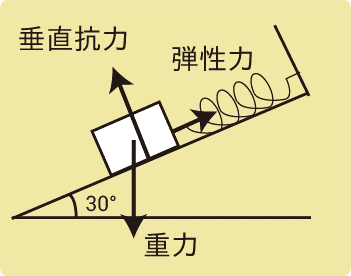
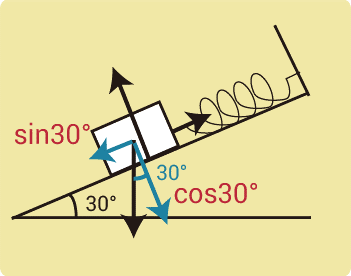
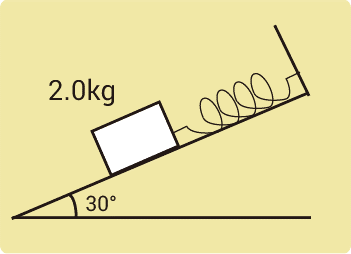
水平とのなす角が30°のなめらかな(摩擦のない)斜面上で、バネ定数196N/mの軽いバネの一端を斜面上端の壁に固定して、他端に質量2.0kgの物体をつけると、バネが伸びて物体が静止した。バネは何m伸びたか。重力加速度の大きさを9.8m/s2とする。
例題3
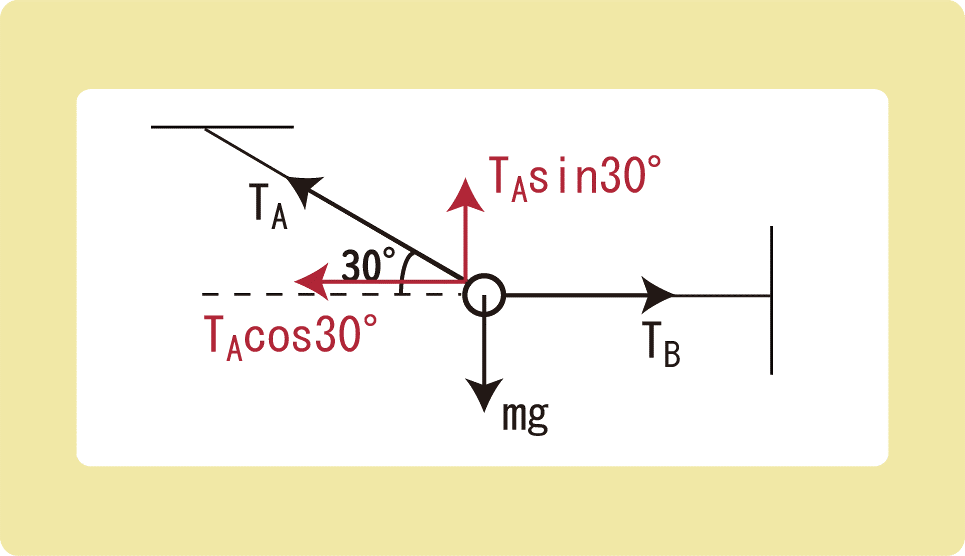
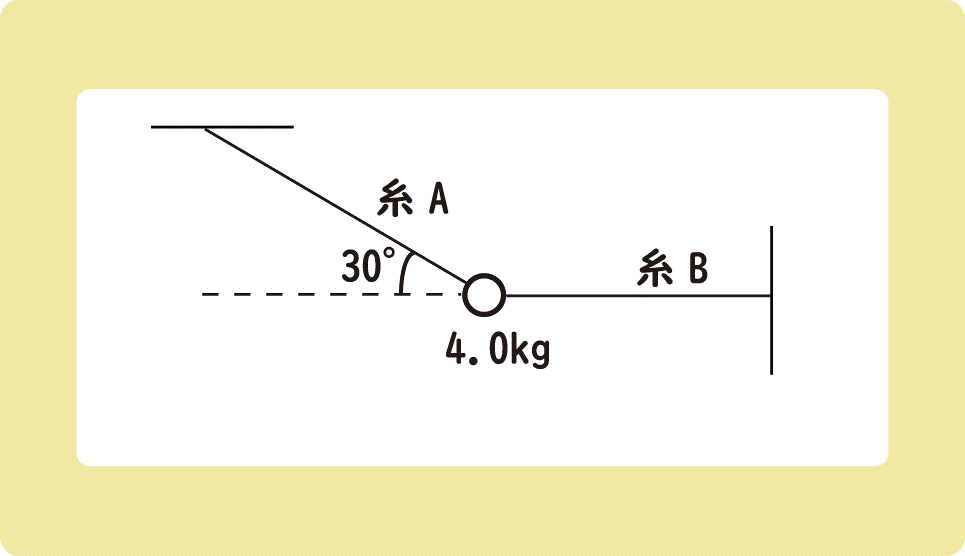
4kgの物体が糸に繋がれ静止している。このとき、糸Aから物体にはたらく張力Aと。糸Bから物体にはたらく張力Bを求めなさい。
まとめ
力のつり合いとは「物体にはたらいている全ての合力=0」のことです。
物体が静止しているときは、力のつり合いを使うのだろうなと必ず疑いましょう。
力が斜めの方向にある場合は上下左右に分解してから考えます。
しかし、斜面に物体が置かれている場合は、斜面の方向に分解した方が簡単に問題を解くことができます。