・静止摩擦力とは
・動摩擦力とは
・摩擦力と運動方程式
摩擦力という言葉は日常でも使うので皆さんご存知ですよね。
物理基礎の力学に登場する力は、重力・張力・垂直抗力・弾性力・浮力に加えて”摩擦力”で最後になります。
摩擦力が分かると、物理基礎の力学の範囲も結構分かってきたということになるので、しっかりと勉強しましょう。
摩擦力とは
面からはたらく物体の運動を妨げる力。
静止摩擦力と動摩擦力の2つに分けて考える。
摩擦力とは、面からはたらく物体を妨げる力のことです。
面というのは壁や地面のことで、どこかに触れていない場合、摩擦力はありません。
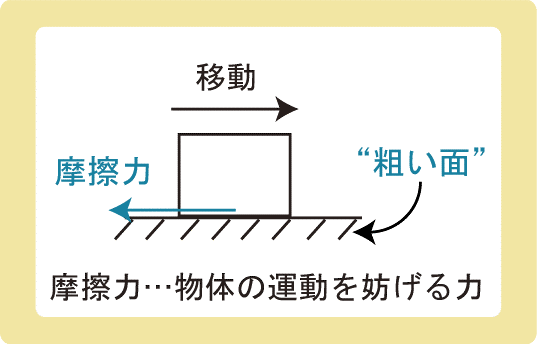
摩擦力は、物体が動こうとするのを邪魔したり、動いている物体を止めたりする力、と考えて大丈夫です。
摩擦力の向きは物体が動いている(動こうとしている)向きの逆向きとなります。
また、摩擦力があるときは問題文に必ず「粗い面」という言葉が書いてあるので、確認しましょう。
(摩擦がない場合は「なめらかな面」と書いてあります。)
物体が静止しているときと動いているときで、静止摩擦力と動摩擦力として分けて考えるので、それぞれ別々に説明していきたいと思います。
摩擦があるときは「粗い面」と書いてあり、摩擦がないときは「なめらかな面」と書いてある
もしどちらも書いていない場合、摩擦はあるものとして考えましょう
静止摩擦力とは
静止中の物体にはたらく摩擦力。
大きさは物体を引く力によって変化する。
物体がすべり出す直前の静止摩擦力。
静止摩擦力の最大値
$$F_0=μ_0N$$
μ(ミュー)：静止摩擦係数(単位なし)
N：垂直抗力［N］
静止摩擦力とは静止中の物体にはたらく摩擦力のことであり、静止摩擦力の大きさは物体を引く力と同じ大きさになります。
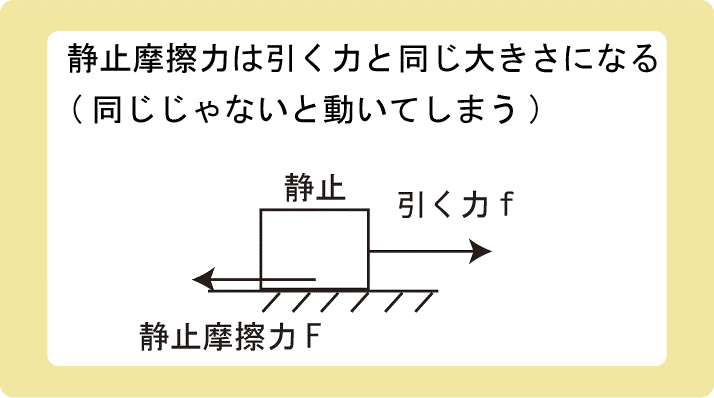
静止摩擦力は物体が滑り出すのを止めるような力であるため、1Nで引っ張れば1Nで邪魔をしますし、20Nで引っ張れば20Nで邪魔をします。
静止摩擦力と物体を引く力が同じ大きさであるため、物体は静止し続けることができるということですね。
しかし、静止摩擦力には限界があり、引く力をどんどん大きくしていくと物体はいつか滑り出します。
このときの摩擦力のことを最大摩擦力といい、記号はF0を使います。(正直、FでもF0でもどっちでもいいです。)
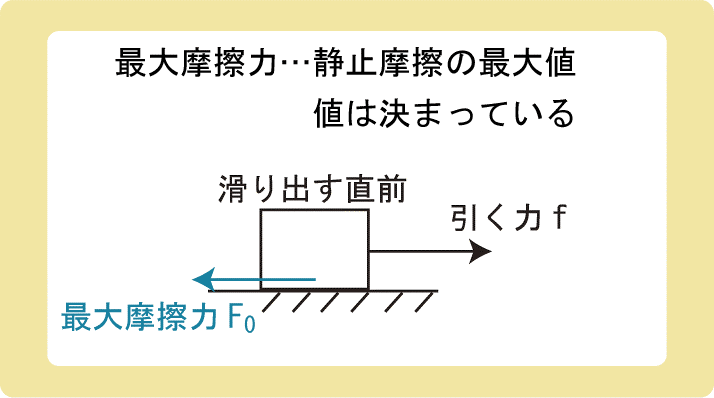
静止摩擦力は物体を引く力によって変化しますが、最大摩擦力の大きさは計算で求めることができます。
静止摩擦係数μ(ミュー)と、垂直抗力Nを使い、
$$F_0=μ_0N$$
という式を使い計算します。
摩擦係数とは、物体の滑りやすさを表す数値です。
氷や油を引いた金属であれば、滑りやすいので摩擦係数が小さくなり、ゴム等の滑りにくい物質は摩擦係数が大きくなります。
また、摩擦係数は0～1の値であるということを知っておくと便利です。
動摩擦力とは
運動中の物体にはたらく摩擦力。
動摩擦力の大きさは常に一定。
$$F’=μ’N$$
μ’(ミュー)：動摩擦係数(単位なし)
N：垂直抗力［N］
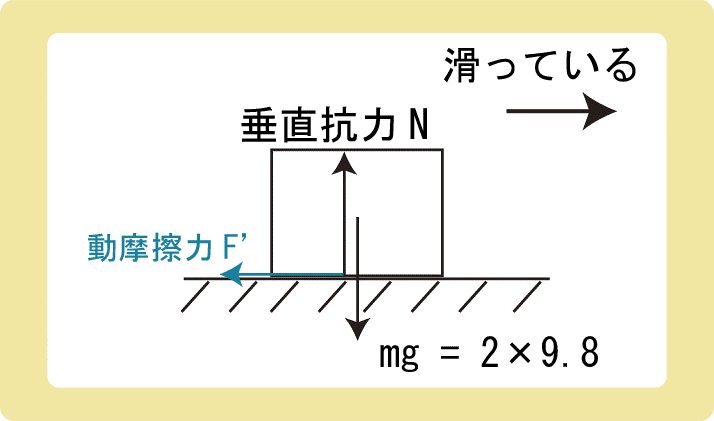
動摩擦力とは、運動中の物体にはたらく摩擦力のことであり、記号F’を使います。
動摩擦力は静止摩擦力とは違い、大きさは常に一定であり、
$$F’=μ’N$$
で求めることができます。
なお、μ’のことを動摩擦係数と言います。
記号が少し違うだけで、最大摩擦力と非常によく似ている式ですね。
最大摩擦力の公式と動摩擦力の公式は、どちらも
$$F=μN$$
となる。
ただし、摩擦係数μは、最大摩擦力と動摩擦力で違う数値を使う。
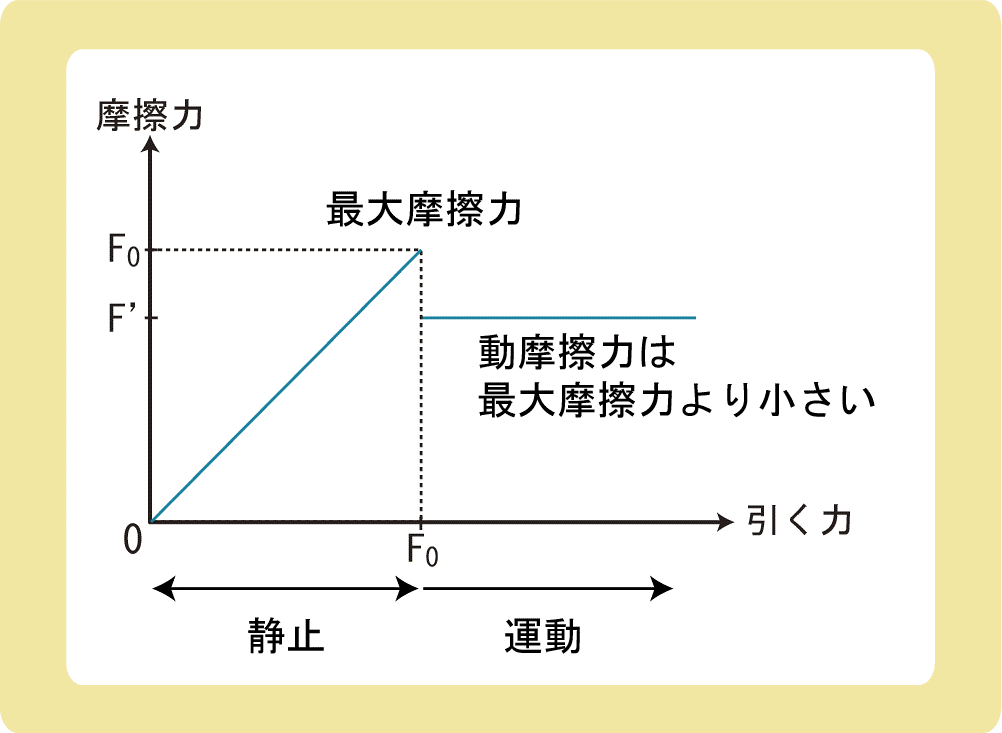
摩擦のある床の上で物体を引くとき、引く力と摩擦力の大きさのグラフは上図のようになります。
静止摩擦力は、引く力が大きくなればなるほど大きくなりますが、いつか限界に達し最大摩擦力になります。
最大摩擦力より大きな力で引くと、物体は動き出し動摩擦力が現れます。
このとき、動摩擦力は一定の大きさであり、最大摩擦力より小さい値となります。
つまり、物体を動かすよりも、動かし続ける方が必要な力は小さいということです。これは日常生活でも感じることですよね。
摩擦力は力の仲間であるため、力のつり合いや運動方程式の問題にも出てきます。
どのような問題があるのか、例題を通して確認していきましょう。
例題
例題1
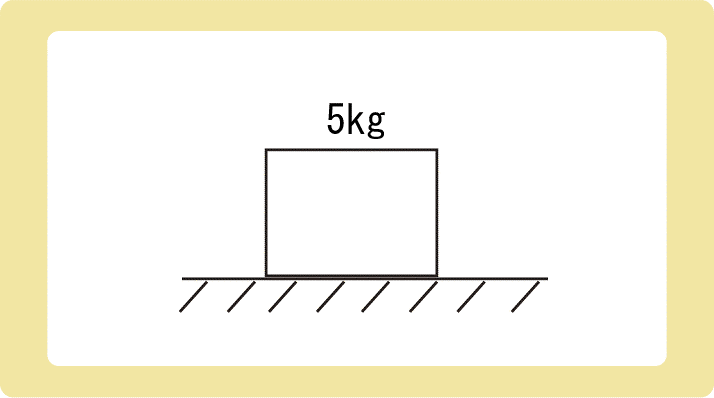
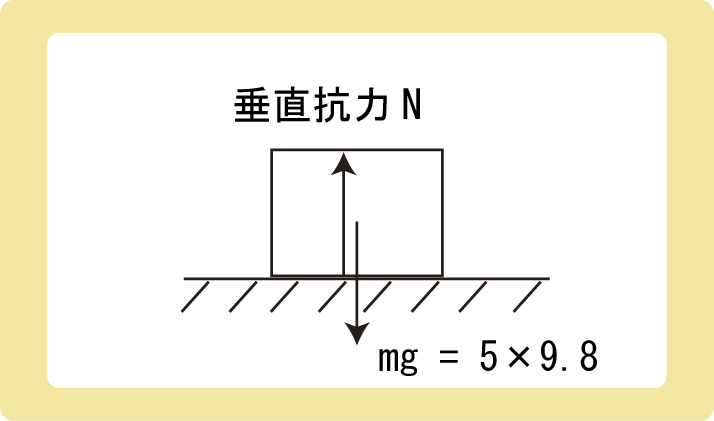
粗い水平面上にある質量5kgの物体を置き、水平方向に引く。引く力の大きさが15Nのとき、物体は動かなかったが、24.5Nをこえたときに滑り始めた。
(1)引く力が15Nのとき、静止摩擦力の大きさは何Nか。
(2)物体と面との間の静止摩擦係数はいくらか。
(1)物体を引いても動かなかったということは、物体を引く力と静止摩擦力の大きさは同じです。
∴15N
もちろん、大きさを聞かれているので向きは答えなくて大丈夫です。
(2)静止摩擦係数を求めるために、公式\(F_0=μ_0N\)を使います。
24.5Nをこえたときに滑り始めたということは、静止摩擦力の限界は24.5Nということなので
$$F_0=24.5$$
となります。
次に、垂直抗力Nは力のつり合いから求めます。
物体は静止しており、力のつり合いより上向きの力＝下向きの力であるため、
\begin{eqnarray}
N&=&mg\\
N&=&5×9.8\\
N&=&49
\end{eqnarray}
となります。
これらの数字を
$$F’=μ’N$$
に代入していくと、
$$24.5=μ’×49\\
μ’=0.5$$
∴0.5
となります。
例題2
粗い水平面上で、質量2.0kgの物体が滑っている。物体と面との間の動摩擦係数が0.30のとき、物体が受ける動摩擦力の大きさは何Nか。また、物体の加速度の大きさは何m/s2か。
動摩擦係数は問題文に書いてあるので、動摩擦力を求めるために垂直抗力を求めましょう。
もちろん、力を図示してから考えます。
粗い水平面上を滑る物体にはたらく力は、重力mg、垂直抗力N、動摩擦力F’の3つです。
物体は運動しているのですが、運動しているのは左右であり上下には運動していないので、上下のみ力のつり合いで立式することができます。
上下の力のつり合いより
\begin{eqnarray}
N&=&mg\\
N&=&2×9.8\\
N&=&19.6
\end{eqnarray}
これを\(F’=μ’N\)に代入すると
\begin{eqnarray}
F’&=&0.30×19.6\\
F’&=&5.88
\end{eqnarray}
∴5.88N
加速度を求めるためには運動方程式を使います。
$$ma=F$$
より、今回移動している方向にはたらいている力は動摩擦力のみなので、
\begin{eqnarray}
2a&=&5.88\\
a&=&2.94
\end{eqnarray}
∴2.94m/s2
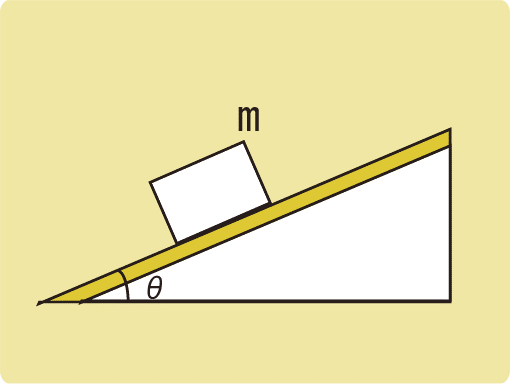
例題3
傾斜角がθである粗い斜面の上に質量mの物体を静かに置いたところ、物体は滑り出した。動摩擦係数をμ’、重力加速度をgとするとき、以下の問に答えなさい。
(1)物体にはたらく動摩擦力の大きさを求めなさい。
(2)物体の加速度の大きさを求めなさい。
まとめ
・「粗い」は摩擦あり、「なめらか」は摩擦なし。
・静止しているときは静止摩擦力、運動しているときは動摩擦力。
・「滑り出す直前」は最大摩擦力。
・公式は$$F=μN$$
今回の解説はこれで終わります。
