・運動方程式とは
・2つの物体の運動方程式
物体が静止していた場合は力のつり合いを使いましたが，動いている物体について考えるときは運動方程式という式を使います。
運動方程式はニュートンの運動の第2法則を式にしたものであり，物理全体を通して最も重要な式と言っても過言ではないくらい大切な式です。
今回もしっかり勉強していきましょう。
運動方程式とは
$$ma=F$$
質量m[kg]の物体にF[N]の力を加えると，力と同じ方向に加速度a[m/s2]が生じる。
運動方程式とは，ニュートンの運動第2法則の「質量m[kg]の物体にF[N]の力を加えると，力と同じ方向に加速度a[m/s2]が生じる」ということを式で表したものです。
運動方程式は非常に単純で，質量mと加速度aと物体にはたらいている合計の力Fを用いてma=Fと表します。
物理基礎だけではなく物理の範囲でもよく使う式なので絶対に忘れてはいけません。
ここで注意するべきことは，運動方程式のFは合力を表しているということです。
また，複数の力がある場合は合成することに注意しましょう。
式の立て方は例題を解きながら確認していきます。
例題
例題1
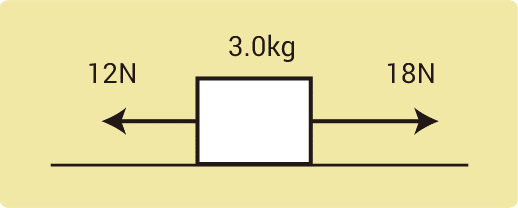
なめらかな水平面上に質量3.0kgの物体が置いてある。水平方向右向きに18N，左向きに12Nの力も加えたとき，物体に生じる加速度の大きさは何m/s2か。
例題2
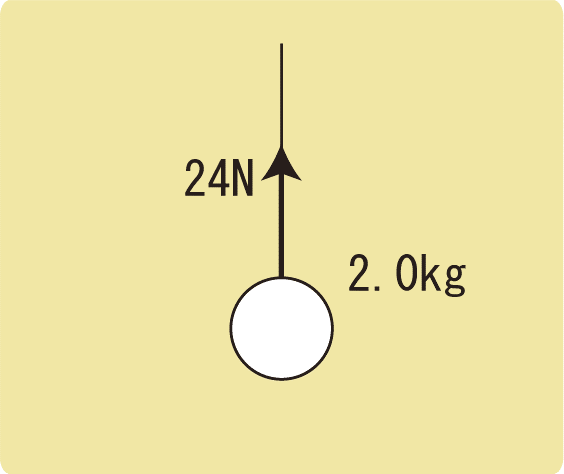
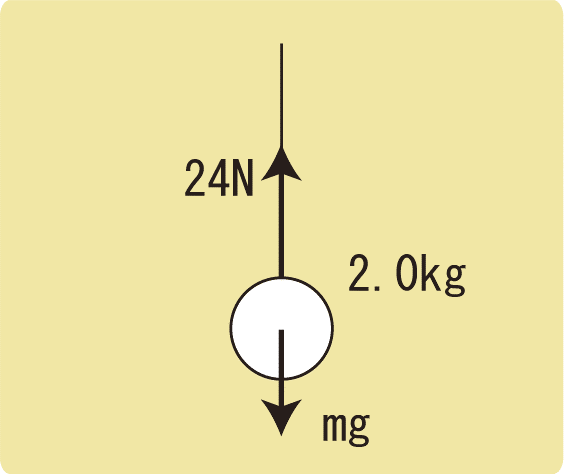
軽い糸に取り付けた質量2.0kgの物体を，鉛直上向きに24Nの力で引き上げた。この物体の加速度の大きさを求めなさい。ただし，重力加速度の大きさを9.8 m/s2とする。
力が登場し，さらに物体が動いている(運動している)ときは，「もしかして運動方程式を使うかもしれないな」と考えましょう。
力だけではなく加速度も登場している場合，運動方程式を使う確率はかなり高いです。
もちろん，この問題でも運動方程式を使います。
運動方程式を使うときに気を付けることは，「運動している方向にはたらく力を全て図示すること」です。
慣れないうちは，物体にはたらく力を全て描きましょう。
mgを描き忘れると答えも変わってしまうので注意が必要です。
運動方程式のFは合力なので，例題1と同様に複数の力がある場合は合成します。
今回は鉛直上向きに動くので，鉛直上向きをプラスとして考えましょう。
\begin{eqnarray}
F&=&24-mg\\
F&=&24-2×9.8\\
F&=&24-19.6\\
F&=&4.4
\end{eqnarray}
Fが分かったので，運動方程式を使います。
\begin{eqnarray}
ma&=&F\\
2a&=&4.4\\
a&=&2.2
\end{eqnarray}
∴2.2m/s2
今回は合力Fを求めてから計算しましたが，一気に計算することが普通なので，
\begin{eqnarray}
ma&=&F\\
2a&=&24-mg\\
2a&=&24-19.6\\
2a&=&4.4\\
a&=&2.2
\end{eqnarray}
と書いてある模範解答が多いです。
例題3
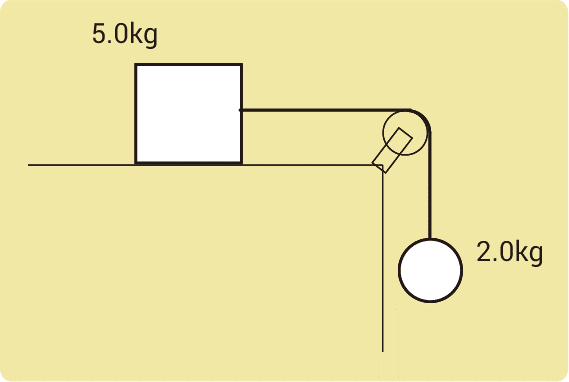
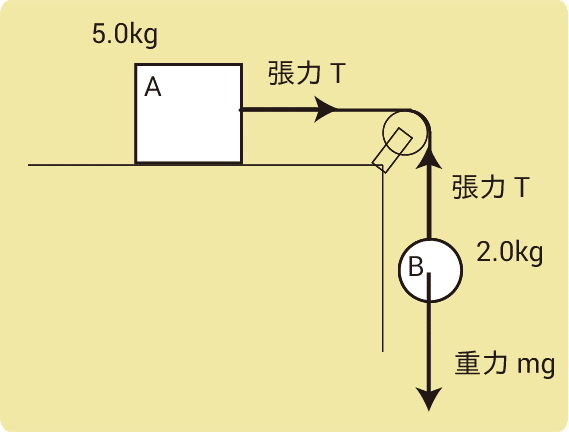
水平でなめらかな机の上に置いた質量5.0kgの物体Aに軽い糸をつけ，それを机の端の滑車に通して，他端に質量2.0kgの物体Bをつるす。静かに手をはなしたところ，2つの物体は運動を始めた。このとき，物体の加速度の大きさは何m/s2か。また，糸が引く力の大きさは何Nか。ただし，重力加速度の大きさを9.8m/s2とする。
まずは力を図示しましょう。
Aは右方向に動くため，重力と垂直抗力は描かなくても大丈夫です。
物体が2つあるとき，それぞれの物体について運動方程式を立て，その2つの式を連立します。
Aは右に動くため右側をプラス，Bは下に動くためBは下側をプラスとして考えます。
また，同じ糸であれば張力Tの大きさは同じなので，T1やT2のように区別しなくても大丈夫です。(糸が複数ある場合は区別しましょう。)
物体Aについての運動方程式
\begin{eqnarray}
ma&=&F\\
5a&=&T…①
\end{eqnarray}
物体Bについての運動方程式
\begin{eqnarray}
ma&=&F\\
2a&=&2×9.8-T…②
\end{eqnarray}
2つの式を連立方程式として解を求めます。
①＋②より
\begin{eqnarray}
7a&=&19.6\\
a&=&2.8
\end{eqnarray}
∴2.8m/s2
さらに，このaを①に代入すると
\begin{eqnarray}
5a&=&T\\
5×2.8&=&T\\
T&=&14
\end{eqnarray}
∴14N
このように，2つの物体が一緒に動く場合は，2つの運動方程式を連立して解けば答えがでます。
どのように計算すればいいのか分からない人もいるかもしれませんが，運動方程式の連立は①と②を足せば大体合ってるので，とりあえず足してみればいいと思います。
実は，2つの物体の運動方程式の問題には，連立する以外にも解き方があります。
それは，「2つの物体1つの物体として考える」ことです。
今回の問題では，5.0kgと2.0kgの物体ではなく，合わせて7.0kgの物体が運動すると考えて，
$$7a=19.6$$
と立式することもできます。
質量は合わせて70.kg，張力Tは内側にはたらく力なので打ち消し合い，右辺には重力だけ残り19.6Nです。
物体を1つとみなすことで簡単に式を作ることもできるのですが，この方法は加速度しか求めることができないので，2つの式を作る方が無難です。
例題4
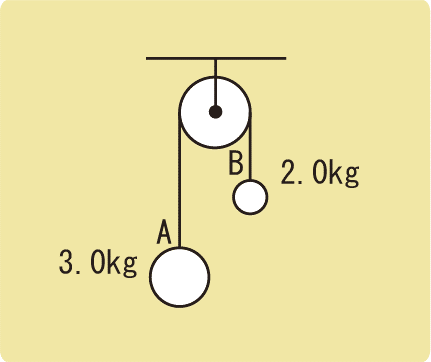
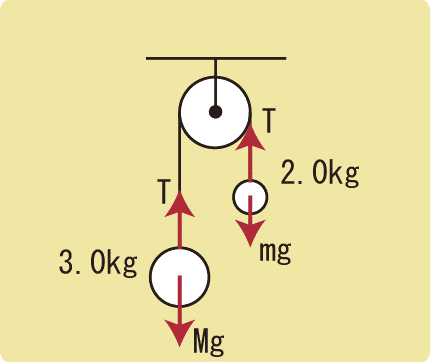
質量3.0kgの物体Aと質量2.0kgの物体Bを軽い糸でつないで滑車にかけ，静かに手をはなすと動き始めた。このとき，物体の加速度の大きさを求めなさい。また，物体にはたらく張力のおおきさを求めなさい。
まずは図に力を描きます。悩む前に，力を描きましょう。
重力は必ず下向き，糸があれば張力Tです。
このような問題も「2つの物体が動いているので運動方程式を2つ作る」と考えましょう。Aは下に動くので下向きをプラス，Bは上に動くので上向きをプラスとします。
なお，質量が2種類あるので，重い方をM，軽い方をmとしています。
物体Aについての運動方程式
\begin{eqnarray}
ma&=&F\\
3a&=&Mg-T\\
3a&=&3×9.8-T\\
3a&=&29.4-T…①
\end{eqnarray}
物体Bについての運動方程式
\begin{eqnarray}
ma&=&F\\
2a&=&T-mg\\
2a&=&T-2×9.8\\
2a&=&T-19.6…②
\end{eqnarray}
2つの式を連立方程式として解を求めます。
①＋②より
\begin{eqnarray}
5a&=&29.4-19.6\\
5a&=&9.8\\
a&=&1.96
\end{eqnarray}
∴1.96m/s2
さらに，このaを①に代入すると
\begin{eqnarray}
3a&=&29.4-T\\
T&=&29.4-3×1.96\\
T&=&29.4-5.88\\
T&=&23.52
\end{eqnarray}
∴23.52N
計算は大変ですが，数学と物理は切っても切れない関係なので，頑張りましょう。
まとめ
運動方程式は
$$ma=F$$
という公式で，力があり運動している場合は運動方程式を使うと考えます。
Fは合力なので，複数の力がはたらいている場合は合成しましょう。
なお，加速していない方向は力がつりあっています。
問題のパターンは様々ありますが，糸で繋がっていたり，物体の上に物体が乗っていたりすることが多いですね。
たくさんの問題を解く必要がありそうです。
