・仕事の原理とは
・「静滑車」と「動滑車」の違い
・仕事率とは
物理において、「仕事」とは「働く」という意味ではなく、「仕事をした」とは「エネルギーを与えた」という特殊な意味を持っているということは前回学習しました。
物理を考えるうえでエネルギーは欠かせない存在ですが、本格的にエネルギーを学ぶ前に「仕事の原理」と「仕事率」を紹介します。
物理基礎を受験で使うのであれば「仕事の原理」は出題されると意外と困る内容であり、物理の内容まで勉強するのであれば「仕事率」を知らないと解けない問題が出てきます。
今回もしっかり勉強していきましょう。
仕事の原理とは
道具を使って仕事をしても、仕事の量は変わらない。
仕事の原理とは、道具を使って仕事をしても、仕事の量は変わらないという原理のことをいいます。
一番理解しやすい例は、自転車のギアについてだと思います。
ギアを重くするとあんまり漕がなくても前に進みますが、ギアを軽くするとたくさん漕ぐ必要がありますよね。
このように、ギアという道具を使っても進むために必要なエネルギーは結局同じであるという考え方が、仕事の原理の考え方です。
しかし、物理基礎の中で仕事の原理としてよく出てくるのは動滑車についての例なので、滑車についての説明をします。
「静滑車」と「動滑車」の仕組み 計算方法
正直、動滑車って言われても全然想像できないですよね。
そもそも滑車とは、糸やロープ等をかけることのできる溝が周囲にある円盤の道具のことであり、
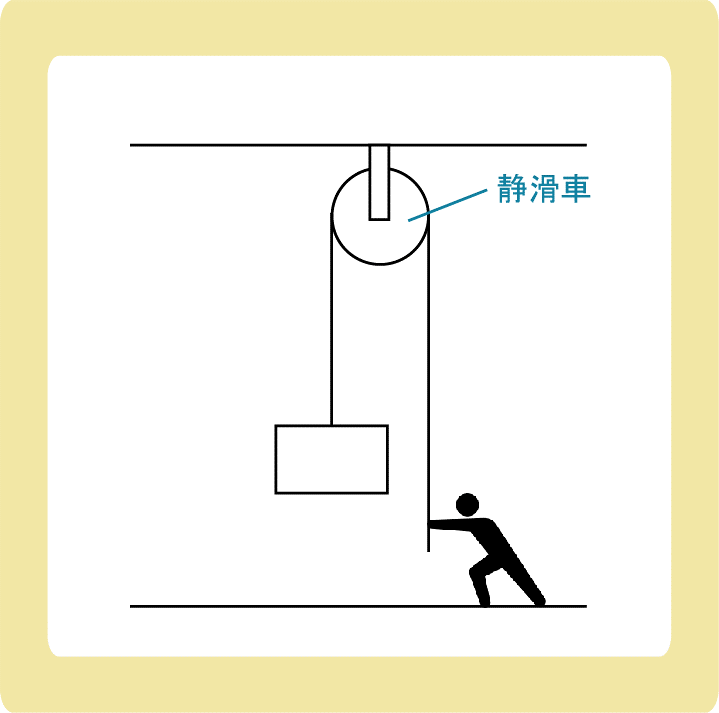
静滑車とは天井等によって固定された滑車のことで、物体を持ち上げるときに使うと便利な道具です。
例えば静滑車を使って物体を10m持ち上げるためにはロープを10m引っ張る必要があるため、静滑車を使って物体を持ち上げるためには、普通に持ち上げるときと同じ大きさの力が必要になります。
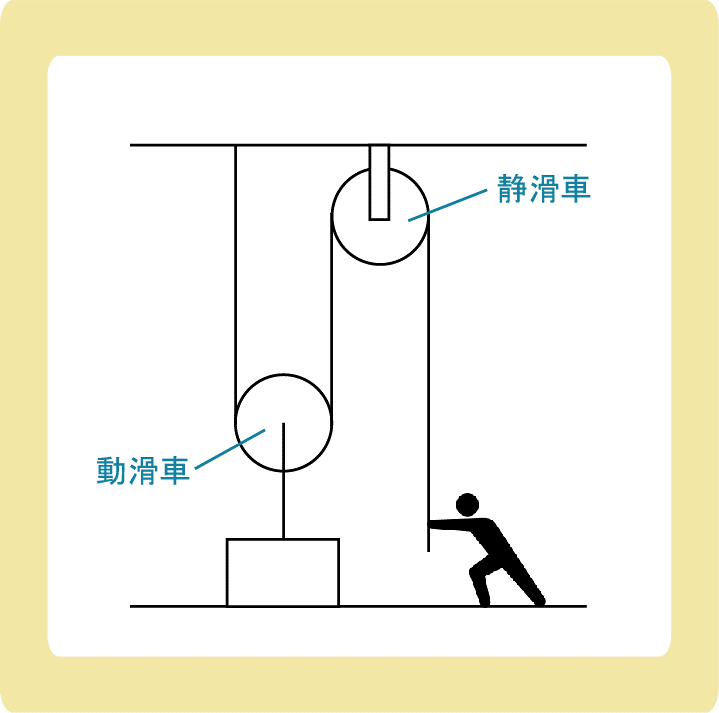
一方、動滑車とは固定されていない滑車のことをいいます。
よく静滑車と一緒に登場しますが、別に静滑車がなくても物体を持ち上げることは可能です。
滑車の数が複数あるとややこしくなってくるので、静滑車と同時に登場させることが多いのでしょう。
物理基礎では、動滑車の重さは軽い(ほぼ0)という設定で出題されることが多いため、動滑車の重さは考えません。
動滑車の最大の特徴は「力を2つに分けることができる」ということです。
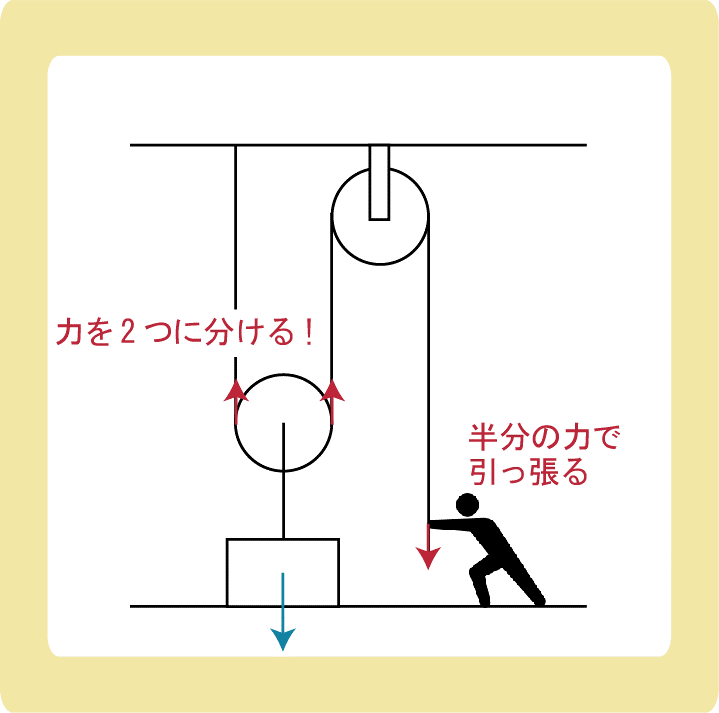
運動方程式の解説でも説明しましたが、「同じ糸(ロープ)であれば力の大きさは等しい」ため、動滑車の左右にある糸にはたらく力の大きさは等しくなります。
(滑車にかかっているため、同じ糸です。)
物体をゆっくり持ち上げるとき、動滑車にかかる力はつり合うため、動滑車の左右の糸にかかる力は物体の半分になり、人が糸を引っ張る力も物体を持ち上げるための力の半分になります。
重いものを持ち上げるとき、動滑車を使うことで簡単に持ち上げることができます。
私は、エレベーターのない狭い建物でちょっとした機器を屋上に持ち上げたいときに動滑車を使いました。実際に使うと分かりますが、結構軽くなる実感がありますね。
動滑車を使うと通常の半分の力で持ち上げることができるのですが、欠点があります。
それは、糸を通常の長さの2倍も引っ張らないといけないという点です。
必要な力は半分になるのですが、引っ張る長さは2倍になってしまうのです。
ここで仕事の公式を思い出しましょう。
$$W=Fs$$
力が半分になっても、糸を移動させる距離が2倍になったということは、力×長さの結果は変わりません。
これが「道具を使って仕事をしても、仕事の量は変わらない」という仕事の原理の仕組みです。
動滑車を使うと半分の力で持ち上げることができるが、2倍の長さを引く必要がある
例題
例題1
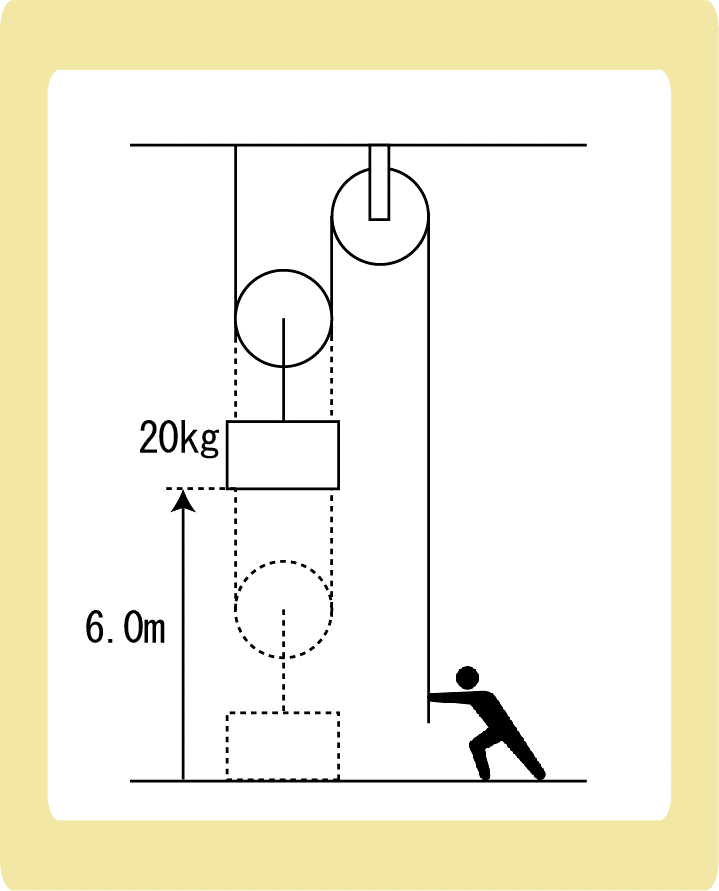
図のように、滑車を用いて質量20kgの物体をゆっくりと6.0m持ち上げた。次の各問に答えなさい。ただし、重力加速度の大きさを9.8m/s2とし、滑車とロープの質量は無視できるものとする。
(1)人がロープを引く力の大きさは何Nか。
(2) 6.0m持ち上げるには、ロープを何m引く必要があるか。
(3)人が物体にした仕事は何Jか。
仕事率とは
1秒あたりの仕事。
\begin{eqnarray}
P&=&\frac{W}{t}\\
P&=&Fv
\end{eqnarray}
仕事率とは、1秒あたりの仕事のことです。
PはPowerの頭文字であり、単位は[W](ワット)です。仕事W[J]とは違うので、注意が必要ですね。
1秒あたりの仕事なので、仕事Wを時間tで割ったものが仕事率になります。
$$P=\frac{W}{t}$$
ここで、仕事の公式と等速直線運動の公式を使って式変形をします。
\begin{eqnarray}
W&=&Fs\\
x&=&vtより
\end{eqnarray}
\begin{eqnarray}
P&=&\frac{W}{t}\\
P&=&\frac{Fs}{t}\\
P&=&F\frac{s}{t}\\
P&=&Fv
\end{eqnarray}
sは移動距離であるため、実質x=vtのxと同じです。距離÷時間=速さなので、P=Fvという式を導くことができます。
仕事率は
\begin{eqnarray}
P&=&\frac{W}{t}\\
P&=&Fv
\end{eqnarray}
と、2つの公式があるので、問題によって使い分ける必要があります。
どちらの公式を使うかは問題によります。どちらの方が多く使うとかはあまりありませんが、物理の電磁気の分野ではP=Fvがたまに出てきますね。
なお、仕事率をPowerの頭文字であるPを使うのは、電力のelectric powerからきています。電気の分野でも説明しますが、電力もP[W]であり、仕事率と同じ記号[単位]となっています。(なので、物理の電磁気分野にも仕事率の公式が登場します)
例題
例題2
次の各問に答えなさい。
(1)4分間に6000Jの仕事をする装置の仕事率は何Jか。
(2)20m/sで等速直線運動をする電車の仕事率が15000Wのとき、電車を動かしている力は何Nか。
まとめ
仕事の原理とは「道具を使って仕事をしても、必要なエネルギーは変わらない」ということです。
坂を使っても滑車を使っても、「力×距離」の結果は変わらないのです。力が少なくなれば、その分距離が伸びてしまいます。
仕事率P[W]は仕事Wを時間tで割ったものなので、
$$P=\frac{W}{t}$$
です。
しかし、式変形することで
$$P=Fv$$
にもなることができるので注意が必要です。なんなら、こっちの方がよく出題されます。












