囚人のジレンマとは何かについて、前回はゲーム理論の超序盤の説明をしました。

なんとなくでもゲーム理論の同時ゲームがどういうものなのか理解していただいたと思うので、今回は囚人のジレンマについての解説をしていきます。
囚人のジレンマとは
前回の記事でも書きましたが、囚人のジレンマとはゲーム理論の中の1つのゲームであり自分の利益を考えた結果にもかかわらず悪い結果になってしまうというジレンマのことを言います。
早速ですが囚人のジレンマを具体的に見ていきましょう。
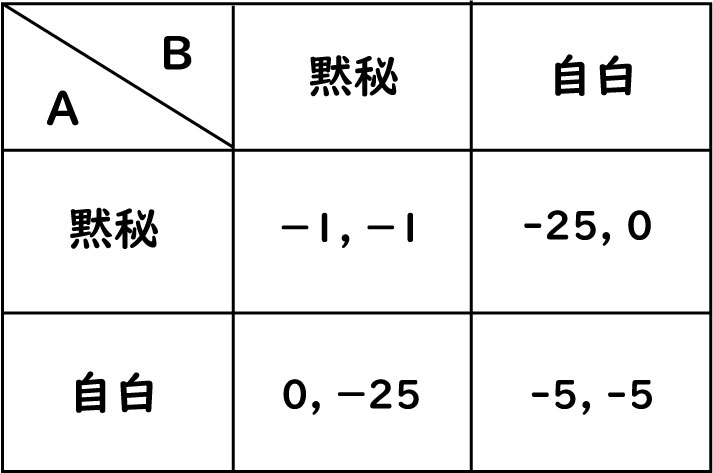
今、2人の人が警察に捕まっています。
2人は警察から自白を迫られており「もし、お前だけが自白したらお前は無罪だ」と取引を持ち掛けられています。
まとめると
①自分だけが自白すれば無罪
②相手だけが自白すれば懲役25年
③お互いに黙秘すればお互い懲役1年
④お互いに自白すればお互い懲役5年
という状況にあります。
もちろん、2人は別室におりもう一人の人が何を選択するかは分からない状態にあります。いわゆる同時ゲームというものですね。
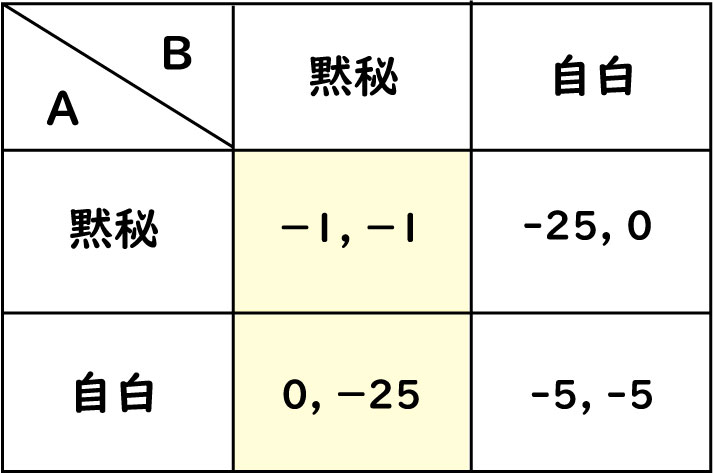
自分が囚人A、相手が囚人Bとします。
相手が黙秘をした場合を考えて見ると、自分は自白した方が罪が軽くなります。
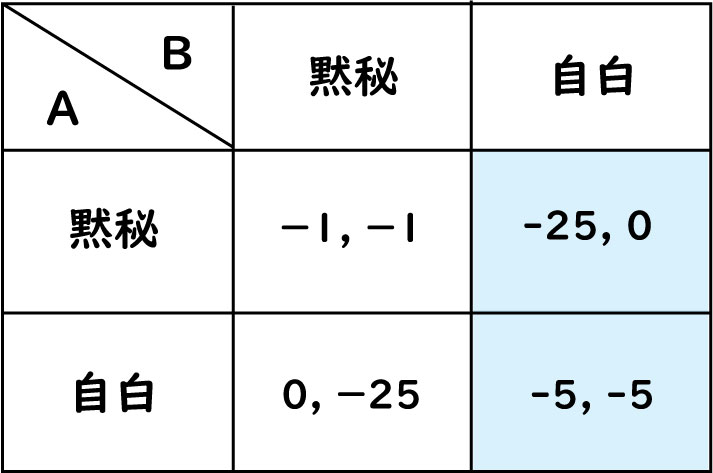
相手が自白した場合を考えても自分は自白した方が懲役が少なくなりますね。
つまり相手がどちらを選択しようと自分は自白した方が良いと考えれます(支配戦略)。
しかし、相手も自分と同じ状況であるため相手も同じように自白を選択します。
その結果はどうでしょうか?
お互いが支配戦略の自白を選択したせいでお互いが黙秘をすることよりも状況が悪くなってしまいました。
自分の利益を考え自白を選択したにもかかわらず、お互いが黙秘を選んだ結果よりも悪くなってしまう。
これが囚人のジレンマです。
世の中には色々な囚人のジレンマが存在しています。
軍拡競争と囚人のジレンマ
囚人のジレンマの具体例で真っ先に思い浮かぶのが軍拡競争についてです。
例えばA国とB国という2つの国が軍拡競争をするかしないかという選択を迫られていたとします。
①自分だけが軍拡すれば優位に立てるので損害0
②相手だけが軍拡すれば脅威に脅かされるので損害25
③お互いに軍拡しなければ少ない防衛費で済むのでお互い損害1
④お互いに軍拡すれば高い防衛費がかさみお互い損害5
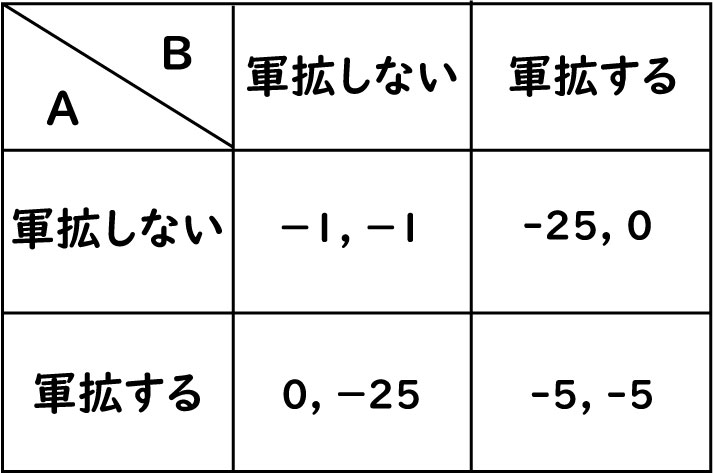
分かりやすくするために先程と同じ数字を使っていますがこれも一種の囚人のジレンマと言えます。
他にも環境問題の対策に協力するか、スマホの通信費を少し安くするか高いままにするか(企業目線)なども囚人のジレンマに当てはめることができます。
これらのような囚人のジレンマを解決するためにはどうしたら良いでしょうか?
囚人のジレンマを解決するためには??
罰金や罰則を設ける
1つ目の方法として罰金や罰則を設けるという方法があります。
どういうルールを追加するのかというと
協定や法律を作り、協力をしない場合に罰金や罰則を与えるようにします。
例えば、先ほどの軍拡競争についてこれ以上の軍拡を行った場合30の罰金や罰則を与える法律を作るとします。
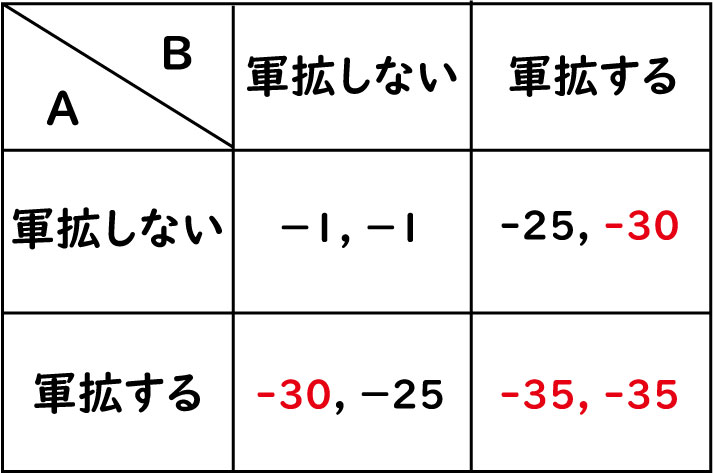
法律や協定のせいで軍拡すると30の損をするので、先程と違い軍拡するとき(-30 or -35)よりも軍拡しない(-1 or -25)の方が良い選択肢となります。
つまり、お互いが「軍拡しない」という選択を取るようになり囚人のジレンマは解決します。
一応「軍拡すると罰金や罰則を設ける」ということに2つの国が合意しなければ成立しないのですが、この条件であれば必ず合意することになるでしょう。
理由は簡単です。
「これ以上の軍拡を行った場合30の罰金や罰則」ということに同意しない場合は囚人のジレンマに陥ってしまい、お互いに損害が5になってしまいますが、
「これ以上の軍拡を行った場合30の罰金や罰則」に同意した場合は軍拡しないという選択肢が最も損害の少ない選択肢となるため、お互いに損害が1で済むようになり同意しない場合よりも損害が少なくなります。
これは「相手が同意をする」ということを知っている交互ゲームの一面も持っているので、交互ゲームと部分ゲームの混合形となっています。
繰り返しゲームを行う
罰金や罰則を設けることで囚人のジレンマを解決することができるように見えましたが、本当にそうでしょうか。
もし協定を破って軍拡してしまった場合、軍事力を持つ国に対して罰金や罰則30を与えることは不可能ではないでしょうか?
実際、2019年8月1日に中距離核戦力全廃条約(INF全廃条約)は失効し、環境問題においても2001年に京都議定書からアメリカが離脱しています。
囚人の場合を考えても、有効な手段がない場合は罰金や罰則が機能しません。
そのような場合、囚人のジレンマを解決するために「繰り返しゲーム」というものを考えます。
繰り返しゲームとは、同じ同時ゲームを何度も繰り返し行うゲームのことをいいます。
先ほどの軍拡競争については1度きりで終わるような内容ではなく、これから先に何度も同じような状況になると考えられます。
交互ゲームの解説をしていないので細かい解説ができないのですが、繰り返しゲームの回数が2回や3回、100回のように数えられる有限の数だと囚人のジレンマは解決しません。
同じゲームが無限に続くときに限り、囚人のジレンマが解決される可能性があります。
繰り返しゲームの特徴は「前回、相手が何を選択したのかを知っている状態」になることです。
繰り返しゲームにおける有名な戦略にトリガー戦略というものがあります。
トリガー戦略とは「最初は協力し、一度でも相手が協力しなかったら、その後は決して協力しない」という戦略です。
永遠に協力しない国 vs. トリガー戦略の国 を考えます。
永遠に協力しない国は最初の一回目だけ少ない損害で済みますが、その後は永遠にお互いが協力し合わないので、大きな損害を出してしまいます。
つまり、こちらがトリガー戦略を選択しているということが相手に伝わっていれば相手は損を出さないため協力せざるを得なくなり囚人のジレンマが解決します。
最初の一回の損害だけを考えている場合はトリガー戦略が通用しませんが、全ての国は現在だけではなく将来にも価値があると考えていると思うため、トリガー戦略は有効な戦略であると言えるでしょう。
この考えは研究発表されたものではなく、研究者の間で民間伝承(フォークロア)として知られていたことからフォーク定理と呼ばれています。
アクセルロッドの実験とオウム返し戦略
最後にゲーム理論の有名な話としてアクセルロッドの実験について説明します。
囚人のジレンマと共に、アクセルロッドの実験も色々な本で小話として出てくる印象があります。
アクセルロッドの実験がどういう実験かというと、
14人の参加者がコンピューターのプログラミングを用いて200回の囚人のジレンマの繰り返しゲームを総当たり戦で行い、総得点が一番高いプログラム(戦略)を考えた人が優勝
という実験です。
そして優勝者のラパポートという研究者が考えた戦略が「最初は協力し、2回目以降は前回に相手が選んだ選択と同じ選択をする」というオウム返し戦略でした。
その後、200人の参加者でもう一度囚人のジレンマ大会を開いたのですが再びオウム返し戦略が優勝しました。
相手が協力したなら次回は協力する、相手が協力しなかったなら次回は協力しない、ということを繰り返すことも囚人のジレンマを解決する1つの方法であると言えますね。
数学を使わない説明であったのでかなり苦しい説明になってしまいましたが、囚人のジレンマの解説は以上とさせていただきます。
皆様の教養が高まったのであれば幸いです。











