・x-tグラフとv-tグラフについて
・平均の速さと平均の速度について
・瞬間の速度について
物体の運動を表すグラフとしてx-tグラフとv-tグラフという2つのグラフがあります。
物理が得意ではない人にとってグラフというものは厄介な相手ではありますが、グラフを読めることはとても大切なことであるため、頑張って勉強しましょう。
ちなみに、x、v、tがそれぞれ変位・速度・時間を表すということを覚えていますか?
もし忘れていたら以前の内容をチラッと確認して思い出してくださいね。


では、x-tグラフとv-tグラフの説明、平均の速さと平均の速度、瞬間の速度のグラフを用いた考え方の解説をしていきます。
x-tグラフとv-tグラフとは
変位xと時間tの関係を表すグラフ。
傾きが速度となる。
速度vと時間tの関係を表すグラフ。
面積が移動距離となる。
物体の運動を表すためにx-tグラフとv-tグラフというものを使います。
具体的に考えると分かりやすいので、
「4秒の間、2m/sで等速直線運動する物体」を例として考えましょう。
この運動をx-tグラフとv-tグラフで表すと下の図のようになります。
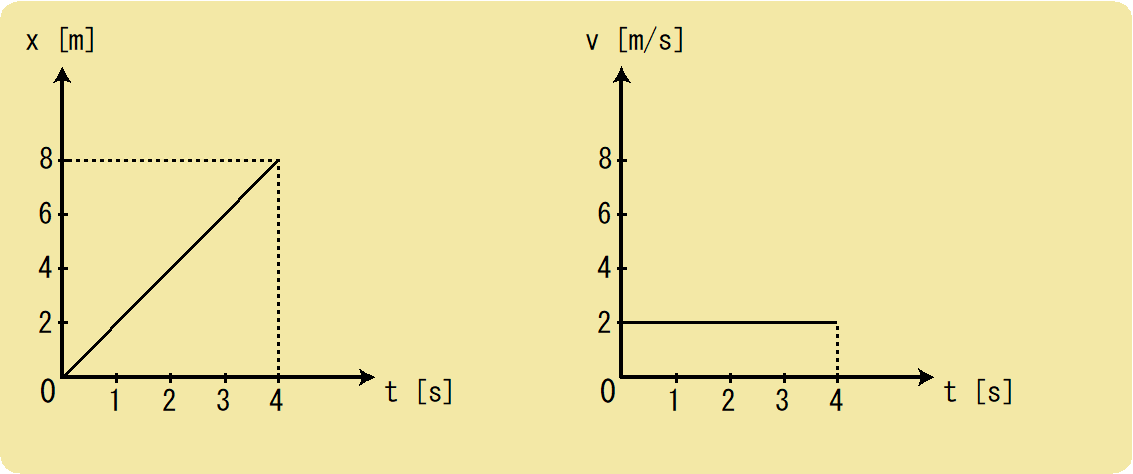
左側にあるグラフはx-tグラフというグラフであり、xとt、つまり、変位と時間を表したグラフとなっています。
4秒、2m/sということは
$$t=4\\
v=2$$
であるため、\(x=vt\)より、
$$x=8$$
となり、4秒間で8m進んだということをグラフで表しています。
グラフが直線なのは等速直線運動だからであり、もし等速でない場合は曲線等になります。
一方、右側にあるグラフはv-tグラフというグラフであり、vとt、つまり、速度と時間を表したグラフとなっています。
グラフが横に真っ直ぐなっているのは等速直線運動だからであり、何秒経っても速度が変わっていないということがグラフから分かりますよね。
もしグラフが増えていたら、それは速度が増えているということです。
x-tグラフの傾きは速度、v-tグラフの面積は移動距離となる
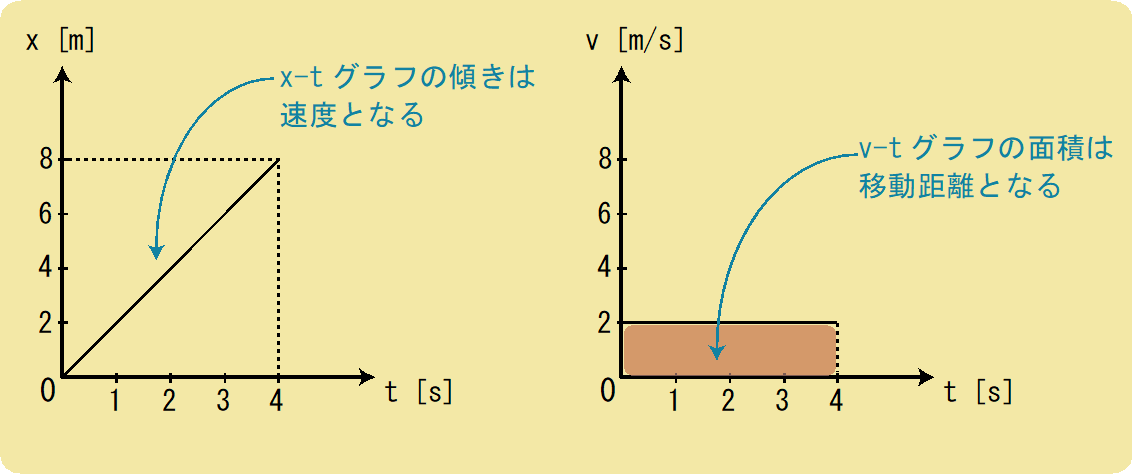
この2つのグラフで知っておくべき点は、上の図の2つにも書いてありますが、「x-tグラフの傾きは速度となる」と「v-tグラフの面積は移動距離」という点です。
グラフの傾きとは中学校数学で習う「xの増加量分のyの増加量」のようなものです。
「どれくらい右に進んで、どれくらい増えたか(減ったか)」のことを傾きといいます。
今回のx-tグラフでは「4進んで8増えている」ので、傾きは\(\frac{8}{4}=2\)となり、その傾きが2m/sという速度になります。
(速度なので、マイナスになる可能性もあります)
上の図の右側を見てください。
色で塗られている面積を計算すると、長方形なので\(縦×横=8\)となります。
v-tグラフでは、軸とグラフでできる図形の面積の大きさが移動距離となります。
平均の速さと平均の速度、瞬間の速度とは
人や物体は常に同じ速度で移動しているわけではありません。
例えば、電車の速度は大体60km/hくらいですが、90km/hで走ることもあれば30km/hで走ることもあります。
ある程度の時間の間での速さ(速度)のことを平均の速さ(速度)
ある時刻における速さ(速度)のことを瞬間の速さ(速度)と言います。
平均の速さと平均の速度の違い
速さと速度の違いを覚えていますか?
速さと速度の違いについて分からなければ、以前の記事を参考にして下さいね。
まず、平均の速さについて説明します。
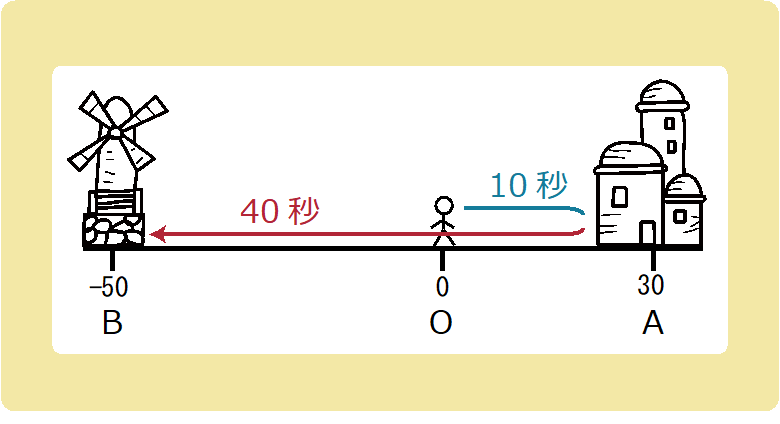
具体的に考えていきましょう。
O→Aと移動するのに10秒、A→Bと移動するのに40秒かかったとします
平均の速さを求めるためには、移動距離と時間を使います。
O→Aの平均の速さは\(x=vtより\)
$$30=v×10\\
v=3$$
となります。
OからAまで速さが一定とは限らないのですが、
移動するのに10秒かかったということは、速さが3m/sくらいだったということだろうと考えるのが平均の速さです。
また、A→Bの平均の速さは\(x=vtより\)
$$80=v×40\\
v=2$$
(ABの長さが80であるので、式の左辺は80としています。)
となり、
O→A→Bの平均の速さは\(x=vtより\)
$$110=v×50\\
v=2.2$$
(O→Bにかかる時間は合計50秒であり、移動距離は110m)
となります。
平均の速さを求めるときはどこからどこまでなのかを必ず指定されるので、その2つの間の距離、時間を使って計算すると良いでしょう。
平均の速さと平均の速度の違いは、速さと速度の違いのように「向きがあるかないか」、つまり、「移動距離なのか変位なのか」という点です。
平均の速度を求めるときは、移動距離ではなく変位を使います。
O→Aの平均の速度は\(x=vtより\)
$$30=v×10\\
v=3$$
これは平均の速さと変わりません。
A→Bの平均の速度は\(x=vtより\)
$$-80=v×40\\
v=-2$$
となります。
平均の速さと違い、左向きに進んでいるため答えはマイナスです。
(問題によっては左向き、西向きという場合もあります。)
O→A→Bの平均の速度は\(x=vtより\)
$$-50=v×50\\
v=-1$$
平均の速度では移動距離ではなく変位を使うため、O→A→Bでの平均の速度を求めるとき、x=-50となります。
これが、平均の速さと平均の速度の違いです。
x-tグラフ問題と瞬間の速度
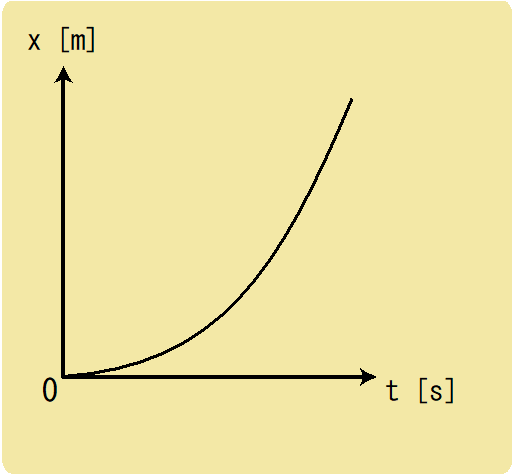
図のようなx-tグラフがあったとします。
x-tグラフが直線ではないということは、この運動は等速直線運動ではないということですね。
この運動は、x-tグラフの傾きが少しずつ大きくなっているので、だんだんと速くなっている運動と言えます。
(後に「加速」として習います。)
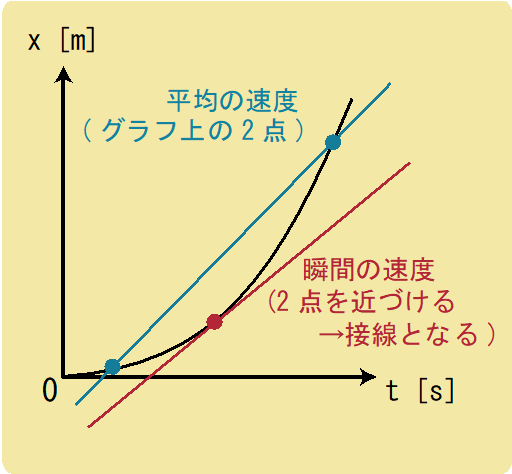
このとき、平均の速度を求めるためにはグラフ上の2つの点を用いて計算をするのですが、この2つの点を限りなく近づけたのが瞬間の速度となるので、2点で作られる直線はグラフの接線となります。
なお、物理基礎の簡単な問題であれば、瞬間の速度を求めるときは必ずx-tグラフに接線が書いてあるので、接線を自分で描く必要はありません。
まとめ
x-tグラフ…傾きが速度となる
v-tグラフ…面積が距離となる
平均の速さ・速度とはある程度の時間の間での速さ(速度)のことであり、瞬間の速さ・速度とはある時刻における速さ(速度)のことです。
平均の速度をグラフから求めるときは、グラフ上の2点を使って計算し、瞬間の速度を求めるときはグラフの接線を使って計算をしましょう。











