・位置エネルギーとは
・重力による位置エネルギーと公式の導出
・弾性力による位置エネルギーと公式の導出
前回は運動エネルギーについて勉強しました。
物理基礎の力学では、運動エネルギーの他にも、位置エネルギーというエネルギーも習います。
ややこしいことに、位置エネルギーにもいくつかの種類が存在しており、異なる公式を使います。
では、今回も物理基礎の勉強をしていきましょう。
位置エネルギーとは
物体がある「位置」にあることによって持つエネルギー。
物理基礎では「重力による位置エネルギー」と「弾性力による位置エネルギー」が登場する。
基準はどこなのかに注意が必要。
位置エネルギーとは、物体がある「位置」にあることによって持つエネルギーのことです。
記号はUを使うのですが、Uは特に何かの頭文字というわけではありません。このように、たまに頭文字でも何でもない記号を使うときもあります。
単位はエネルギーなので[J]です。
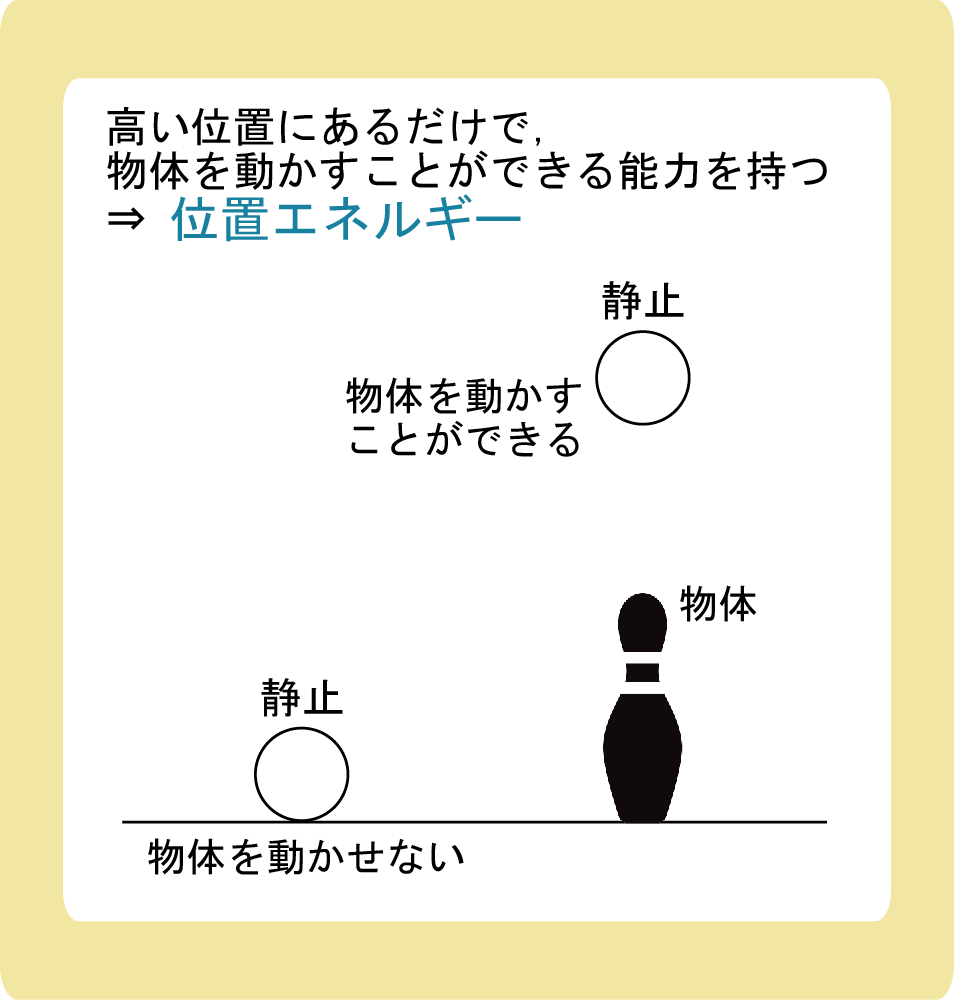
エネルギーとは「物体を動かすことができる能力」のことでしたよね。
動かしたい物体と同じ高さにある静止している球は、物体を動かすことはできません。
しかし、物体の上にある球は、静止していたとしても、落とすことで物体を動かすことができるので、エネルギーを持っていると考えます。
このような、「とある位置にいるだけで、物体を動かすことのできる能力を持つ」ことを、位置エネルギーと呼びます。
あなたが今いる場所は、最寄り駅から〇〇kmの位置でもあり、地球の中心から〇〇kmの位置でもあり、太陽からだと約1億4960万kmの位置にいます。
「位置」には必ず「基準」というものが必要です。
これから登場する「重力による位置エネルギー」では「どこからの高さなのか」という基準を考える必要がありますし、「弾性力による位置エネルギー」では「どこからの長さなのか」という基準を考えなくてはいけません。
それでは、それぞれの位置エネルギーについて紹介します。
重力による位置エネルギーとは
物体が高いところにあるときに持つ位置エネルギー。
$$U=mgh$$
(h:高さ[m])
重力による位置エネルギーとは、物体が高いところにあるときに持つエネルギーのことです。位置エネルギーなので記号はU、単位はもちろん[J]です。
重力による位置エネルギーの公式は\(U=mgh\)なのですが、なぜmghなのかはグラフを見ると分かります。
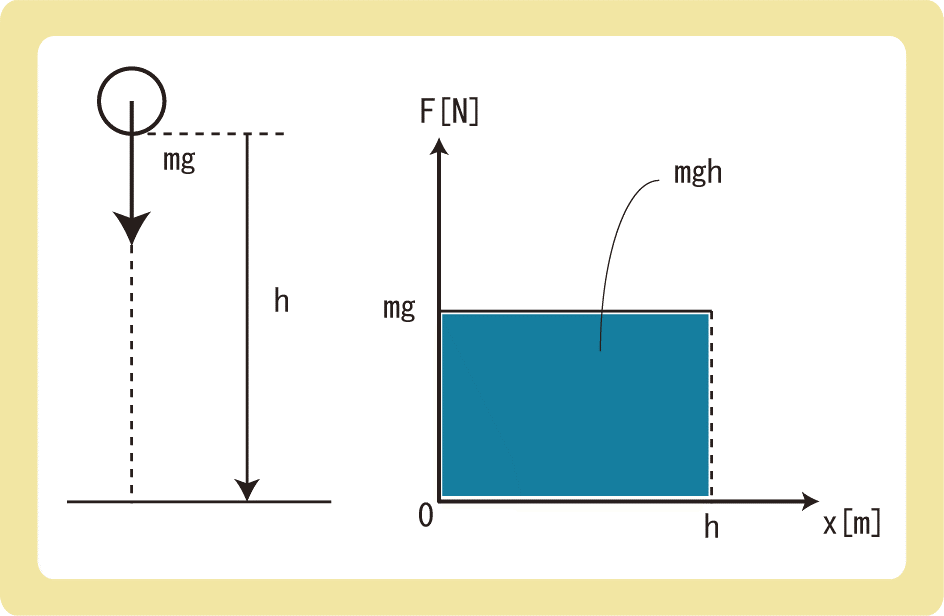
地面を基準としたとき、地面から高さh[m]の場所に質量m[kg]の物体を静かに落としたとします。
物体は一定の力mg[N]でh[m]引っ張られるため、力が物体に仕事をします。
このときの仕事の大きさは
$$W=Fs\\
W=mg×h\\
W=mgh$$
となります。
mghの仕事をされるということは、物体がh[m]落下するとmghだけエネルギーが増えるということになります。
もちろん、物体が落下する前は、物体にまだ仕事がされていない状態なのですが、落下させることによっていつでも物体に仕事をすることができます。
つまり、物体は高いところにあるだけで、いつでもmghの仕事ができる=mghのエネルギーを持っている、と言えるというわけです。
縦軸が力F、横軸が距離xのグラフで表すと、重力は常に一定の大きさであるためグラフは直線になります。
仕事は「力×距離」であるため、グラフの面積が位置エネルギーとなり、mghと一致しますね。
重力による位置エネルギーでは、「どこからの高さなのか」という基準を考える必要があります。問題で指定されていれば問題に従いますが、問題で指定されていない場合、高さの基準を好きなように決めて計算しても大丈夫です。
次回の内容の「力学的エネルギー保存の法則」では、高さの基準を自分で決める場合が多いため、自分で基準を決めるパターンは次回紹介します。
例題
例題1
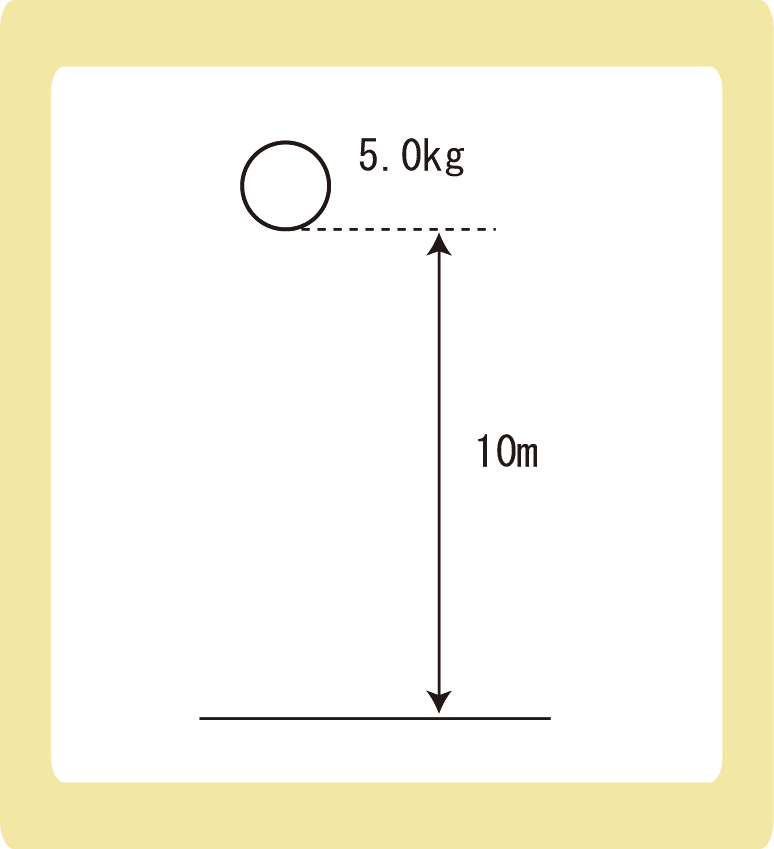
地面から高さ10mの位置にある質量5.0kgの物体の重力による位置エネルギーは何Jか。ただし、重力加速度の大きさを9.8m/s2とし、地面を高さの基準とする。
例題2
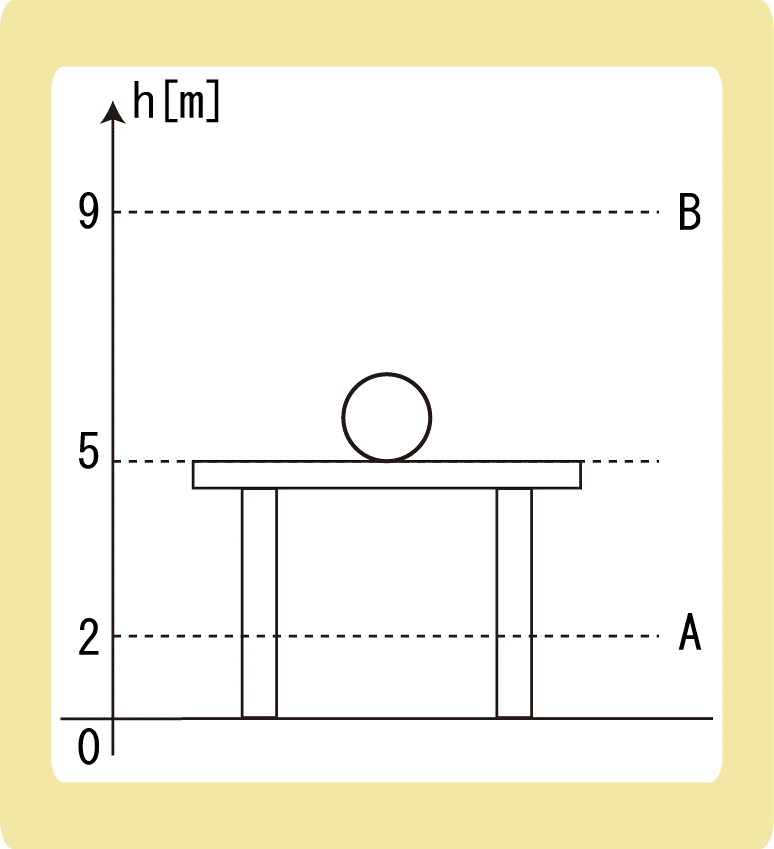
図のように、質量2.0kgの物体が地面から高さ5.0mの机の上に置かれている。次の各問に答えなさい。ただし、重力加速度の大きさは9.8m/s2とする。
(1)高さAを基準面としたとき、物体の持つ重力による位置エネルギーは何Jか。
(2)高さBを基準面としたとき、物体の持つ重力による位置エネルギーは何Jか。
(1)机の上面を基準面としたとき、物体の持つ重力による位置エネルギーは何Jか。
弾性力による位置エネルギーとは
バネを伸ばしたり縮めたりするときに持つ位置エネルギー。
$$U=\frac{1}{2}kx^2$$
(k:バネ定数[N/m] x:バネの伸び縮み[m])
弾性力による位置エネルギーとは、バネを伸ばしたり縮めたりするときに持つ位置エネルギーのことです。
重力による位置エネルギーと同様に、記号はU、単位は[J]となっています。
バネだけではなくゴムなどでも弾性力はあるのですが、高校物理に登場する弾性力を持つ物体の99%はバネなので、弾性力による位置エネルギー=バネのエネルギー、と思いましょう。
ちなみに、残りの1%はゴムです(ゴムはバネと違って伸びるけど縮まない)。
公式は\(U=\frac{1}{2}kx^2\)となるのですが、どうしてこの式になるかも、重力による位置エネルギーと同様にグラフを見ると分かりやすいです。
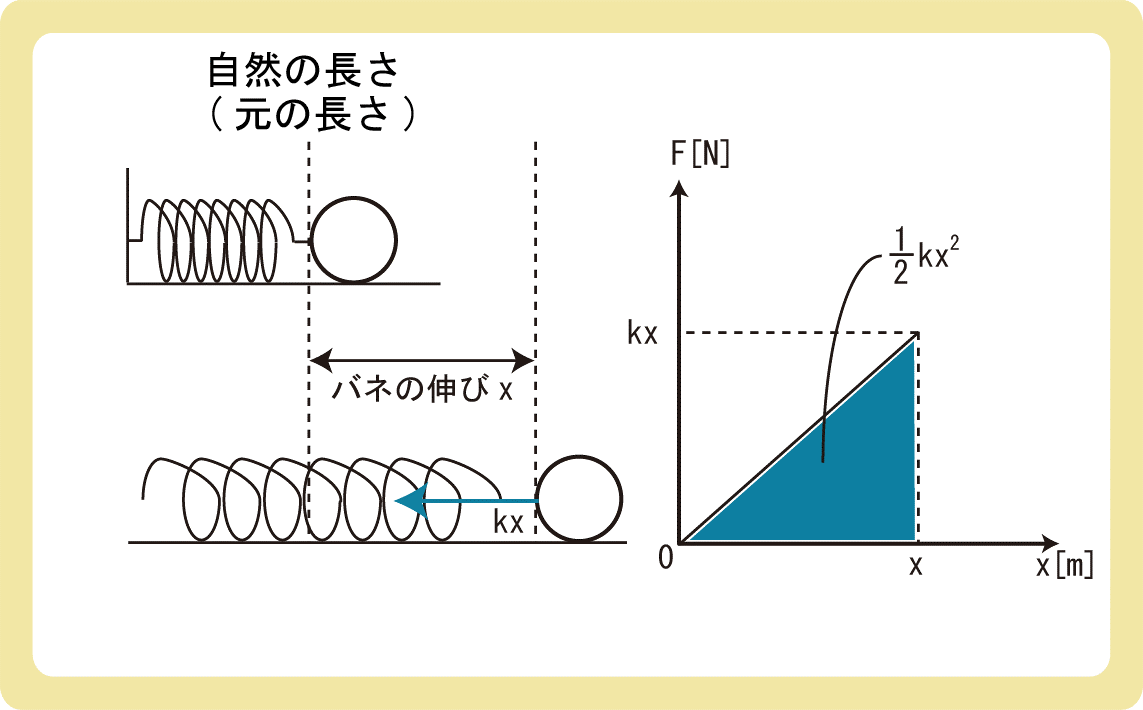
バネをx[m]伸ばすと、弾性力kx[N]がはたらきます。
重力と違い、弾性力は伸ばせば伸ばすほど大きくなるので、単純にkx×xと考えてはいけません。
仕事の公式\(W=Fs\)は、一定の力のときにしか使えないのです。
しかし、縦軸が力F、横軸が距離xのグラフでは、力×長さの和が面積になっているため、グラフの面積がエネルギーの大きさと一致します。
グラフの面積は三角形なので、面積を計算すると
$$U=\frac{1}{2}kx^2$$
という式が出てきますね。
バネの場合、伸びても縮んでもいない自然の長さを基準とすることが多いですが、場合によっては他の場所を基準とするときもあります。
問題を解いて慣れていきましょう。
例題
例題3
バネ定数100N/mのバネが、自然の長さから0.50m押し縮められている。バネにつながれた物体がもつ弾性力による位置エネルギーは何Jか。
例題4
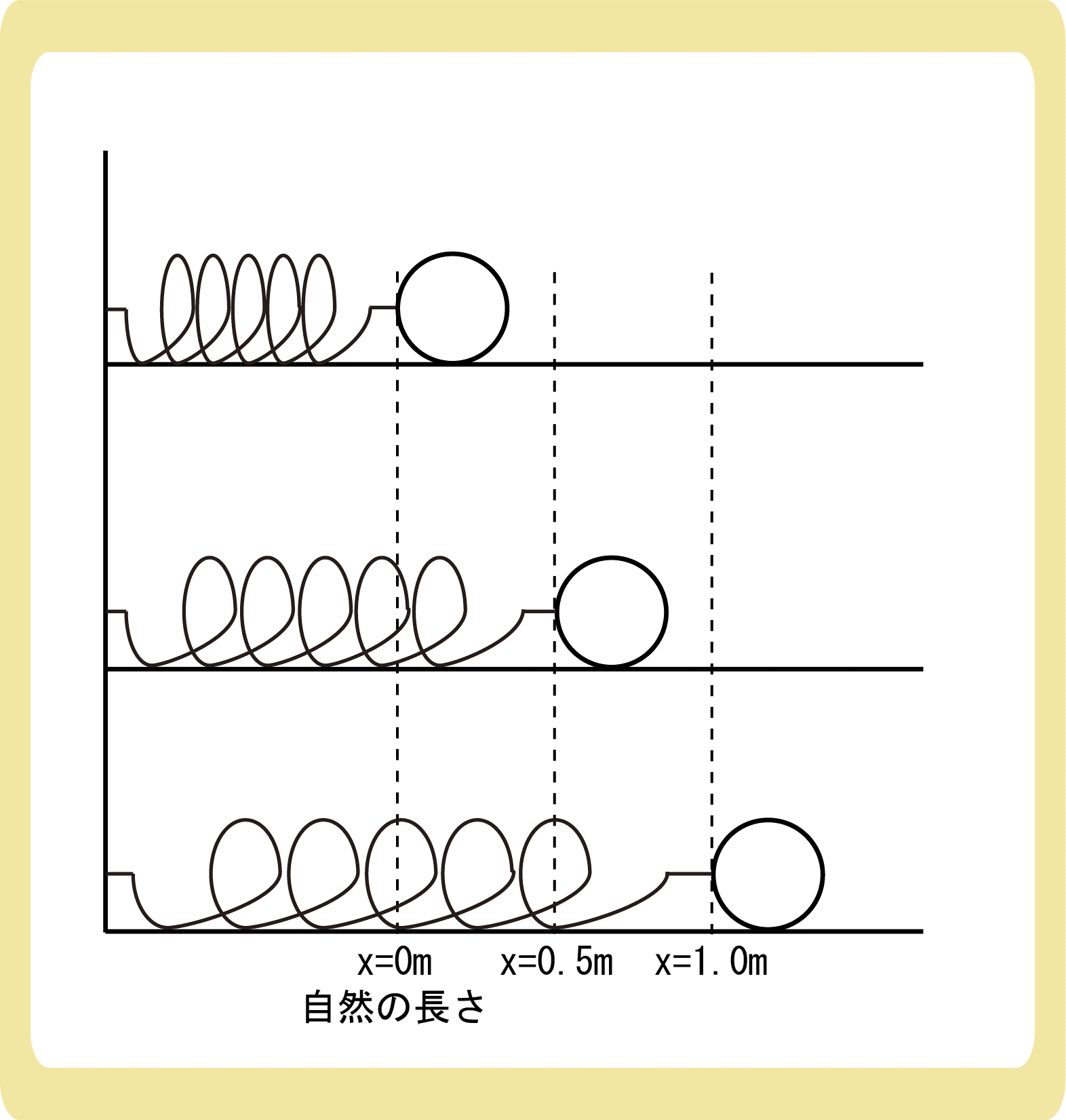
図のように、バネ定数500N/mのバネを、自然の長さから0.50m伸ばす。このバネをさらに0.50m伸ばすためには、外部の力は何Jの仕事をする必要があるか答えなさい。
まとめ
物理基礎に出てくる位置エネルギーは2種類あります。
高いところにあるだけでエネルギーを持っていると考える、重力による位置エネルギー
$$U=mgh$$
と、
バネやゴムが伸びたときにエネルギーを持つと考える、弾性力による位置エネルギー
$$U=\frac{1}{2}kx^2$$
です。
前回の内容でもあった運動エネルギーと合わせて使うことが多いので、とりあえず公式を覚えておきましょう。












