・力学的エネルギー保存の法則とは
・力学的エネルギー保存の問題の解き方
・力学的エネルギー保存と摩擦力
前回と前々回で運動エネルギーと位置エネルギーを勉強しました。
今回は、物理基礎の中で1番重要な「力学的エネルギー保存の法則」について解説します。
高校物理で一番よく使う式は「力学的エネルギー保存の法則」と言っても過言ではありません。
それほど重要な内容なので、しっかり勉強しましょう。
力学的エネルギーとは
運動エネルギー＋位置エネルギーのこと。
力学的エネルギーとは、運動エネルギーと位置エネルギーの和のことです。記号はenergyのE、単位はもちろん［J］ですね。
ただ2つのエネルギーを足しただけなのですが、力学的エネルギーを使うと、曲面上を動く物体や振り子の運動など、直線以外の運動での位置や速さを簡単に求めることができます。
さっそく、力学的エネルギーの使い方を見ていきましょう。
力学的エネルギー保存の法則とは
物体に保存力のみがはたらくとき、物体のもつ力学的エネルギーは一定となる。
$$K+U=一定$$
力学的エネルギー保存の法則とは、物体に保存力のみがはたらくとき、物体のもつ力学的エネルギーは一定となるという法則のことです。
保存力とは重力や弾性力のことで、要は摩擦や空気抵抗がない運動であれば力学的エネルギーは一定ですよという意味です。
仕事の原理というものを覚えていますか？
動滑車を使っても、結局必要なエネルギーは変わらないという例を勉強したと思います。
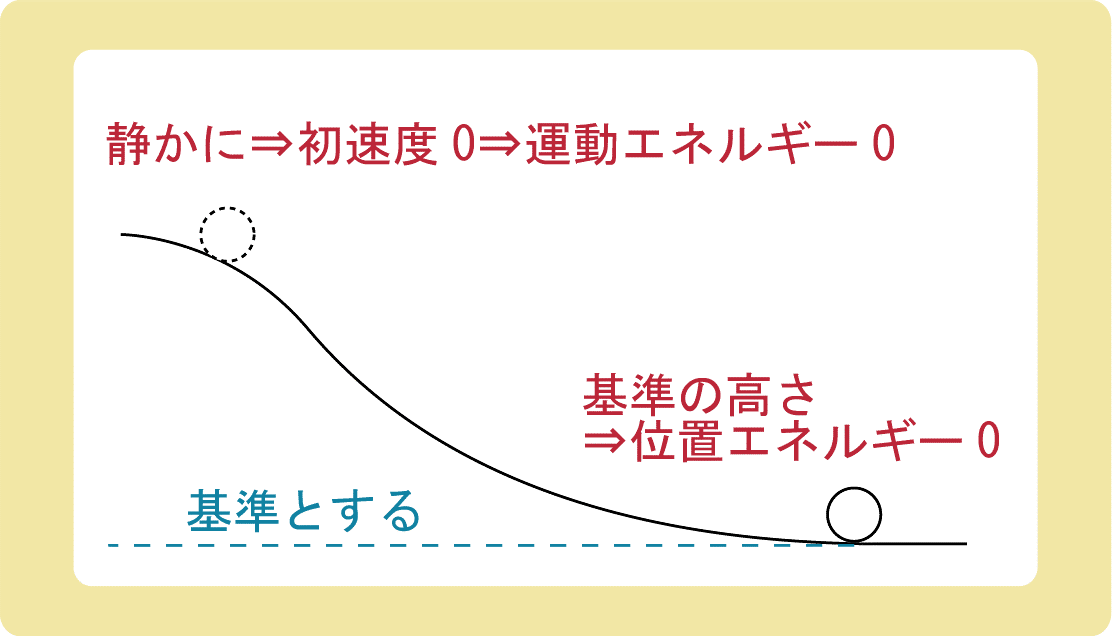
ボールを坂の上で転がしたとき、青い坂でも黄色い坂でも、床にたどりついたときの速さは同じです。(たどり着くまでにかかる時間は変わりますが…)
どのようなルートで移動しても物体に与えたエネルギーが同じになるような力のことを保存力といいます。
物理で登場する保存力は、重力・弾性力・静電気力あたりですね。
上でも説明した通り、摩擦や空気抵抗がなかったり、急に光ったり音を出したり熱を出さなければ、エネルギーは保存します。
力学的エネルギーが一定ということなので、公式は\(K+U=一定\)となります。
Kは運動エネルギー、Uは位置エネルギーであり、
$$K=\frac{1}{2}mv^2\\
U=mgh\\
U=\frac{1}{2}kx^2$$
ということをちゃんと覚えていますか。
Uは2つありますが、高さが関係するときがmgh、バネが出てきたときが\(\frac{1}{2}kx^2\)ですよ。
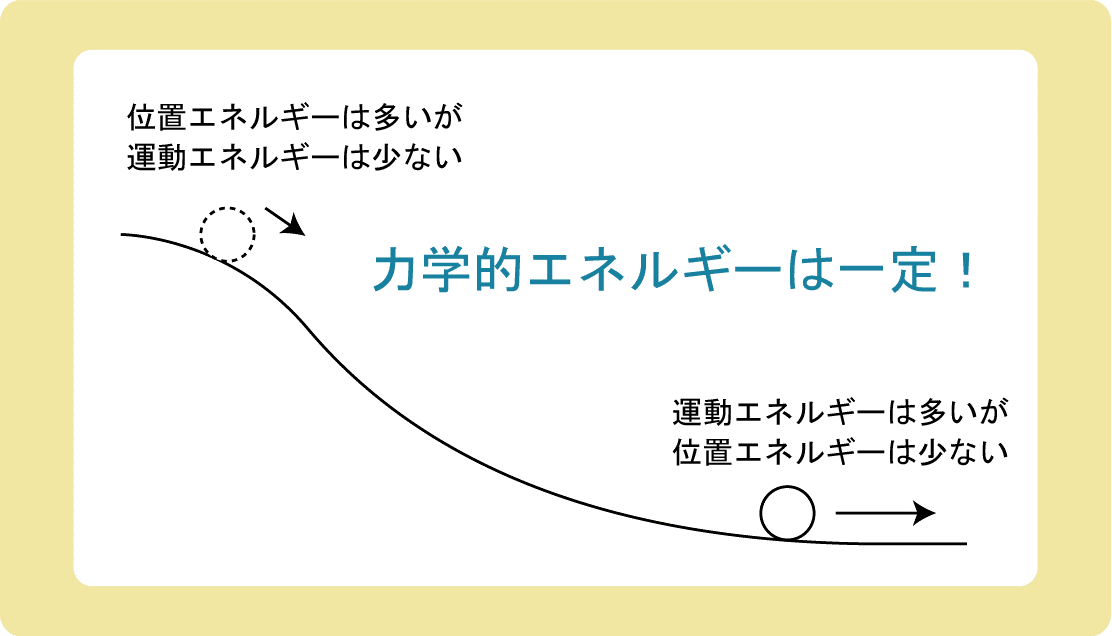
イメージでいうと、高いところにある物体の位置エネルギーは大きいですが、運動エネルギーは小さいです。
一方、低い位置にある物体の位置エネルギーは小さくなってしまいますが、その代わり運動エネルギーが大きくなります。
このとき、位置エネルギーが減った分、運動エネルギーが増加するので、この2つの和である力学的エネルギーは変わらないというのが、力学的エネルギー保存の法則の考え方というわけです。
もちろん、空気抵抗や摩擦がないという前提であり、もし空気抵抗や摩擦があった場合は力学的エネルギーが減ってしまいます。(その代わり、熱などの別のエネルギーになります)
力学的エネルギー保存の法則では色々な問題が出題されるので、例題を通して理解を深めていきましょう。
例題
例題1
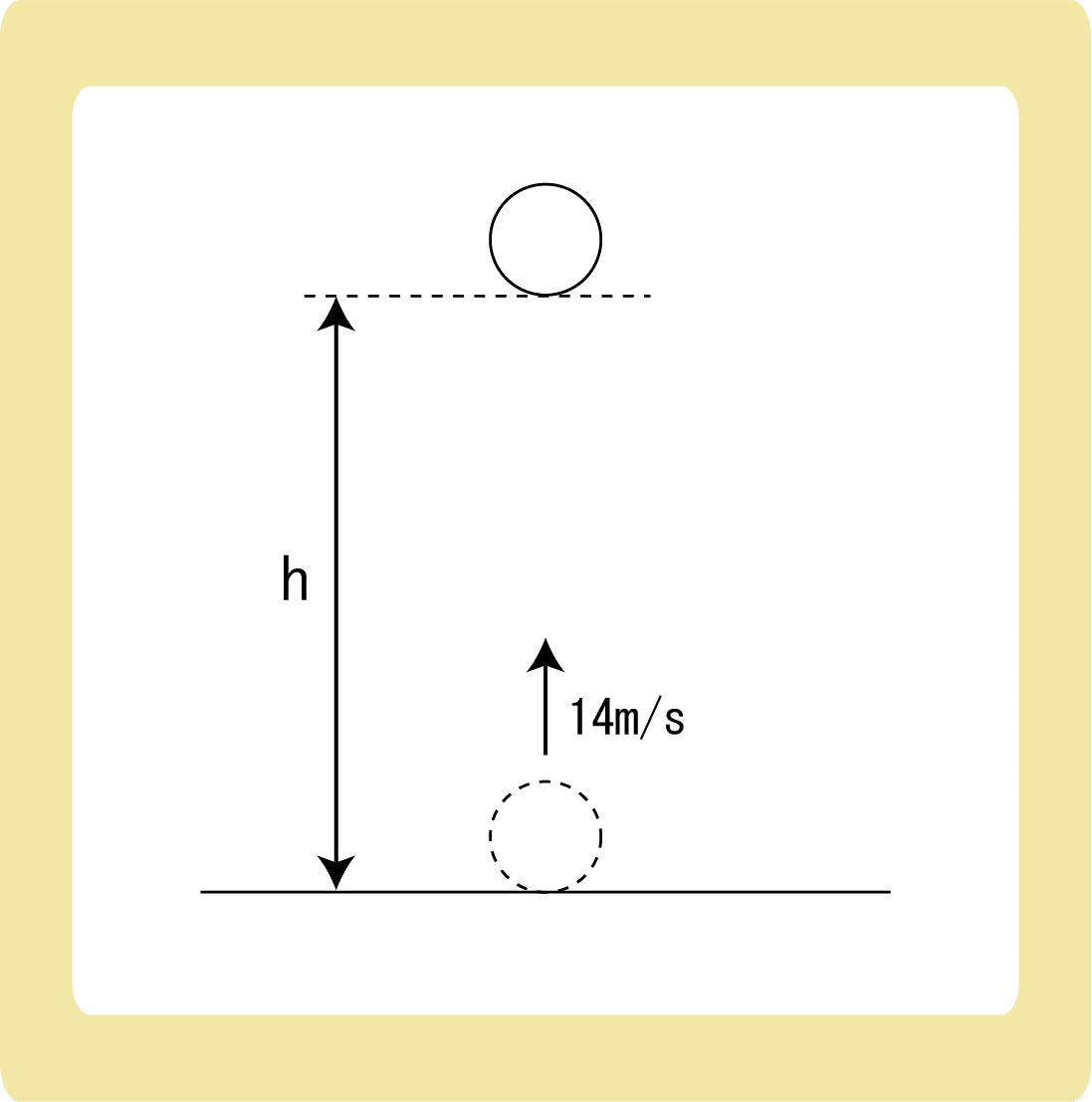
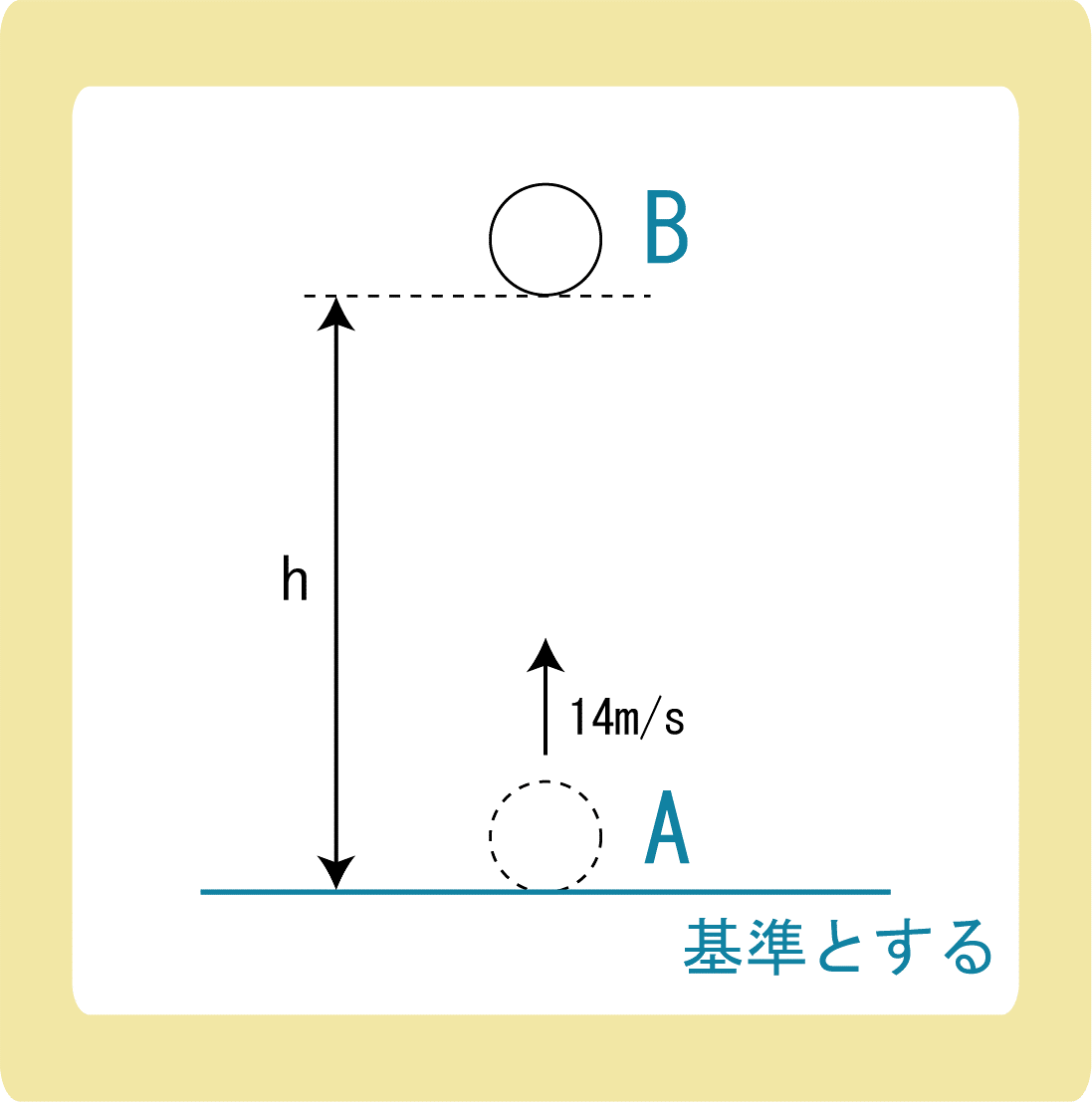
物体を初速度14m/sで鉛直上向きに投げ上げた。このとき、物体の最高点高さは何m/sとなるか。ただし、重力加速度の大きさを9.8m/s2とする。
この問題は力学的エネルギー保存の法則を使わなくても解くことができます。
等加速度直線運動の問題として、
$$v=v_o+at\\
x=v_ot+\frac{1}{2}at^2$$
を使っても解くことができます。
このように、物体がまっすぐ動く場合、力学的エネルギー保存の法則使わなくても問題を解くことはできるのですが、敢えて力学的エネルギー保存の法則を使って解くことも可能です。
力学的エネルギー保存の法則を使うときは、2つの状態のエネルギーを比べます。
今回は、物体を投げたときと、最高点に達したときのエネルギーを比べましょう。
物体を投げたときをA、最高点に達したときをBとするとし、Aを重力による位置エネルギーの基準とすると
Aの力学的エネルギーは
となります。
質量は問題に書いていないので、勝手にmとしています。
こちらで勝手にmを使っているので、解答にmを絶対に使ってはいけません。
(途中式にmを使うのは大丈夫)
また、Aを高さの基準としているので、Aの位置エネルギーは0となります。
高さの基準が問題文に明記されていないときは、自分で高さの基準を決めましょう。床を基準とするのが一番簡単です。
Bの力学的エネルギーは
となります。
Bは最高点にいるので、速さは0m/sですよ。覚えていますか？
力学的エネルギー保存の法則より、力学的エネルギーの大きさは一定なので、
\frac{1}{2}m×14^2=m×9.8×h\\
\frac{1}{2}×14^2=9.8×h\\
\frac{1}{2}×14^2=9.8×h\\
98=9.8h\\
h=10$$
∴10m
この問題が、力学的エネルギー保存の法則の一番基本的な問題です。
例題2
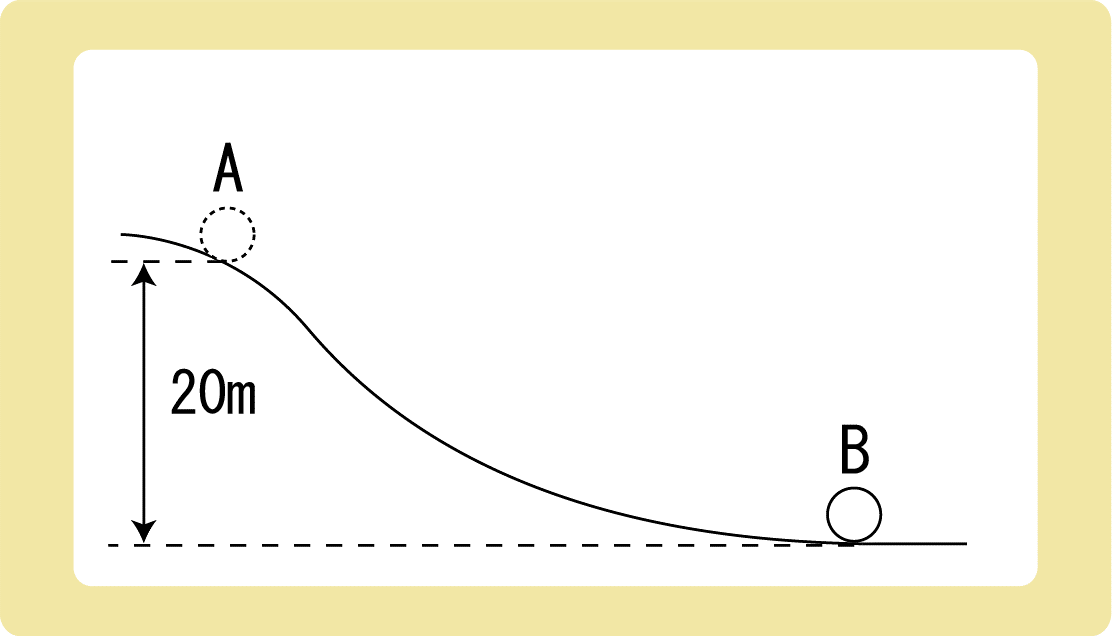
図のように、なめらかな曲面上の点Aから静かに滑り始めた。物体が点Bまで移動したとき、物体の速さは何m/sか。ただし、重力加速度の大きさを9.8m/s2とする。
この問題は、等加速度直線運動や運動方程式では解くことができません。
物体が直線ではない動きをする場合、力学的エネルギー保存の法則を使うことで物体の速さを求めることができます。
力学的エネルギー保存の法則を使うためには、2つの状態を比べなければいけません。
今回は、AとBの力学的エネルギーを比べましょう。
まず、Bの高さを基準とします。
Aは静かに滑り始めたので運動エネルギーは0J、Bは高さの基準の位置にいるので位置エネルギーが0です。
力学的エネルギー保存の法則より
\frac{1}{2}m×0^2+m×9.8×20=\frac{1}{2}m{v_B}^2+m×9.8×0\\
m×9.8×20=\frac{1}{2}m{v_B}^2\\
9.8×20=\frac{1}{2}{v_B}^2\\
392={v_B}^2\\
v_B=±14\sqrt{2}$$
∴\(14\sqrt{2}\)m/s
力学的エネルギー保存の法則はvが2乗であるため、答えが±となります。
しかし、速さは速度と違って向きを考えないため、マイナスにはなりません。
もし速度を聞かれた場合は、図から向きを判断しましょう。
例題3
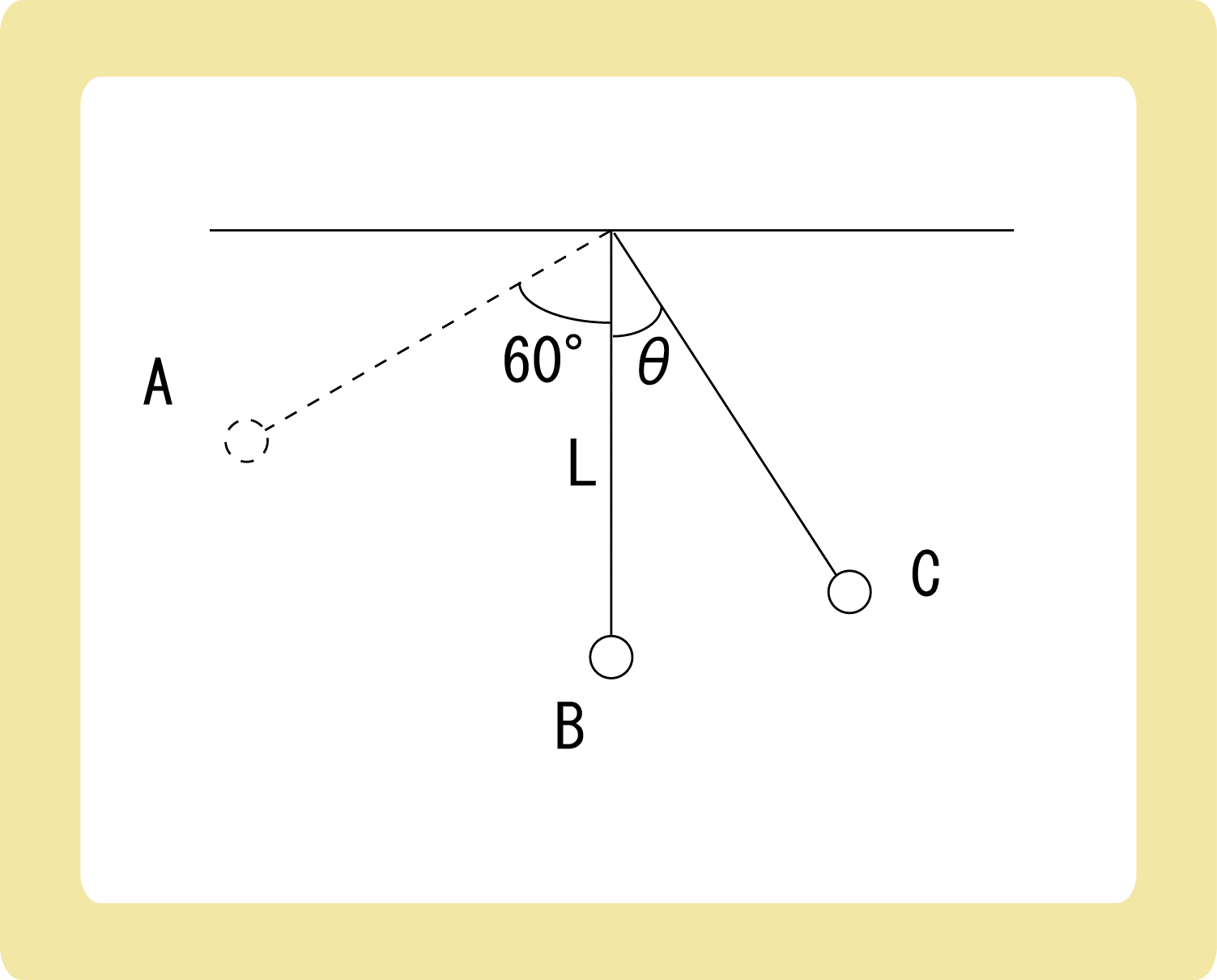
図のように、長さがLの軽い糸におもりをつけ、物体を糸と鉛直方向になす角が60°の点Aまで持ち上げ、静かに離した。物体は再下点Bを通過した後、糸と鉛直方向になす角がθの点Cも通過した。以下の各問に答えなさい。ただし、重力加速度の大きさをgとする。
(1)点Bでのおもりの速さを求めなさい。
(2)点Cでのおもりの速さを求めなさい。
振り子の運動も直線の運動ではないため、力学的エネルギー保存の法則を使って速さを求めしょう。
今回も、一番低い位置にあるBの高さを基準とします。
なお、問題文にはL、g、θしか記号がないため、答えに使えるのはこの3つの記号だけです。
もちろん、途中式であれば他の記号を使っても大丈夫です。
(1)
Bを高さの基準とした場合、Aの高さは分かりますか？
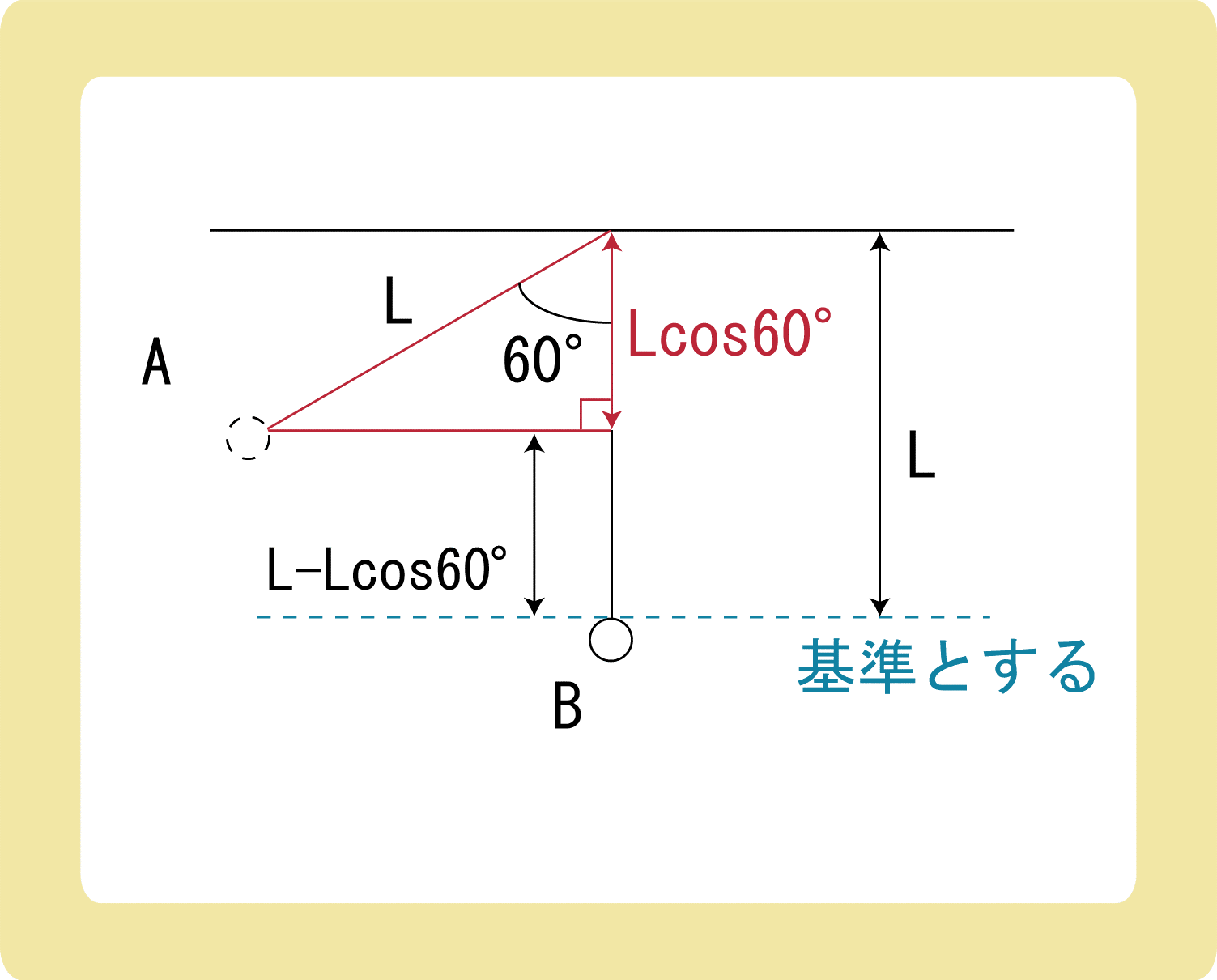
糸の長さがLなので、点Aまでの長さもLです。
AとBの角度が60°なので、図のように直角三角形を作ると、図の赤い矢印で表した長さがLcos60°になります。
$$L\cos60°=L×\frac{1}{2}$$
なので、Aの高さは
$$L- \frac{1}{2}L=\frac{1}{2}L$$
となります。
力学的エネルギー保存の法則より、AとBを比べると、
\frac{1}{2}m×0^2+mg×\frac{1}{2}L =\frac{1}{2}m{v_B}^2+mg×0\\
\frac{1}{2} mg L =\frac{1}{2}m{v_B}^2\\
g L ={v_B}^2\\
v_B=\sqrt{gL}$$
∴\(\sqrt{gL}\)
となります。物理の円運動の基本問題にも良く出てくる内容ですね。
逆にいうと、物理でも物理基礎の力学的エネルギー保存の法則をよく使うということです。
(2)点Cの速さを求めるためには、もちろん力学的エネルギー保存の法則を使うのですが、力学的エネルギーは”保存”しているため、比べる相手はA・Bのどちらでも大丈夫です。
問題によって、使いやすい方を選びましょう。
もし(1)を間違ってしまった場合を考えると、AとCで比べるのが無難だと思います。
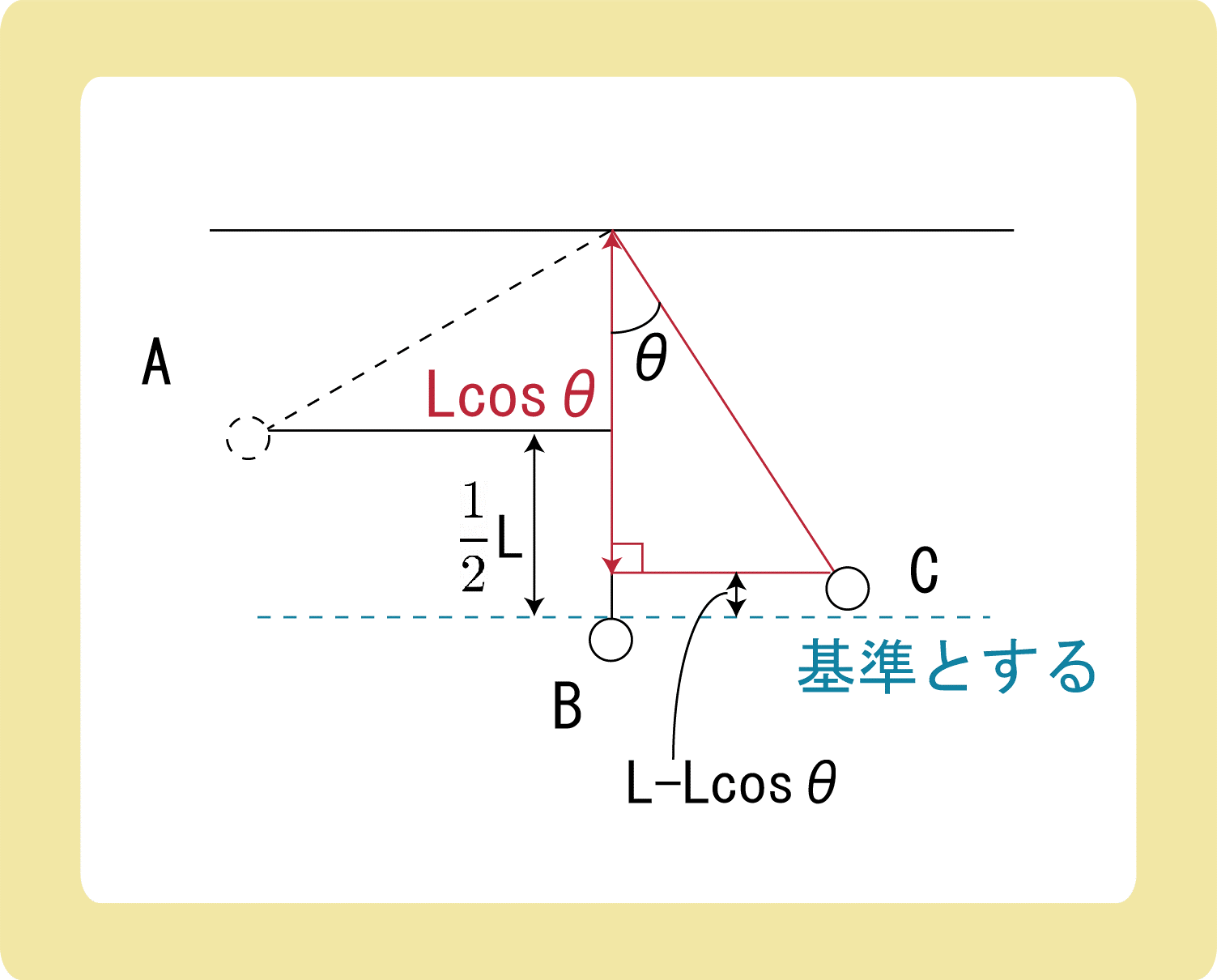
(1)と同様に、Bを高さの基準としてCの高さを考えます。
これまた(1)と同様に、図の赤色の直角三角形を考えると、赤い矢印の長さはLcosθとなります。
従って、Cの高さはL-Lcosθとなります。
力学的エネルギー保存の法則より、AとCを比べると、
\frac{1}{2}m×0^2+mg×\frac{1}{2}L=\frac{1}{2}m{v_C}^2+mg×(L-L\cosθ)\\
mg×\frac{1}{2}L=\frac{1}{2}m{v_C}^2+mg×(L-L\cosθ)\\
g×\frac{1}{2}L=\frac{1}{2}{v_C}^2+g×(L-L\cosθ)\\
gL={v_C}^2+2gL(1-\cosθ)\\
{v_C}^2=gL-2gL(1-\cosθ)\\
{v_C}^2=gL-(2gL+2gL\cosθ)\\
{v_C}^2=-gL+2gL\cosθ\\
{v_C}^2=gL(2\cosθ-1)\\
v_C=\sqrt{ gL(2\cosθ-1)}$$
∴\(\sqrt{ gL(2\cosθ-1)}\)
となります。
実際、θ＝60°を代入するとv=0になりますし、θ=0°を入れると(1)の答えになります。
例題4
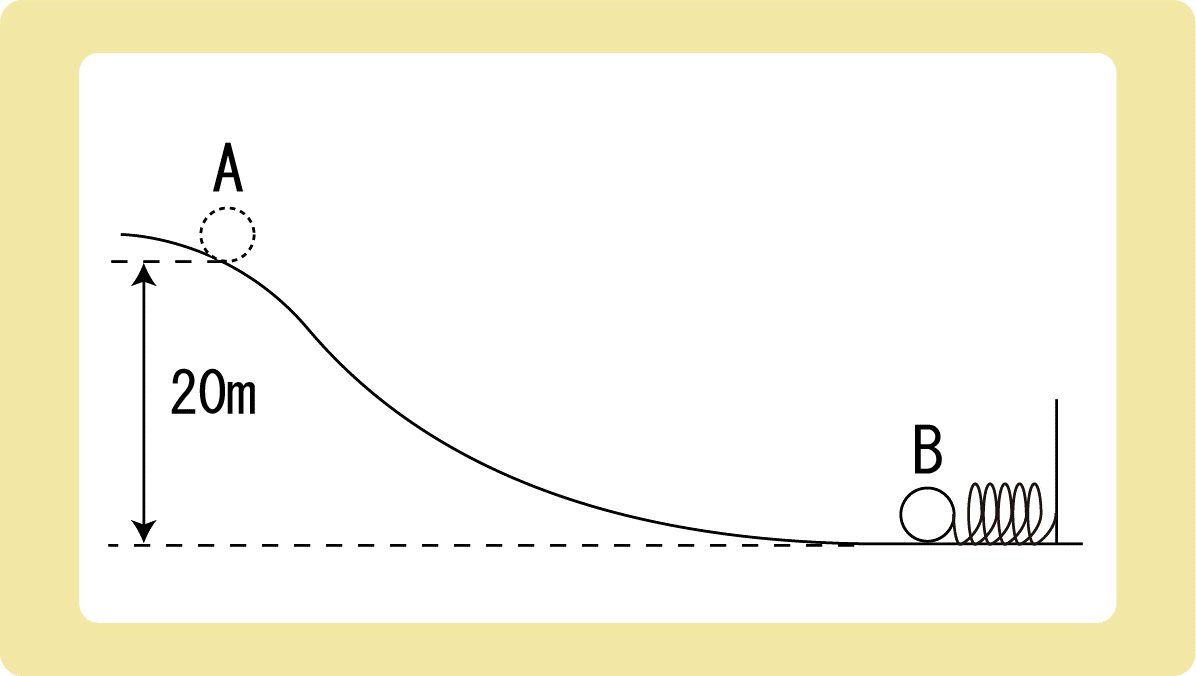
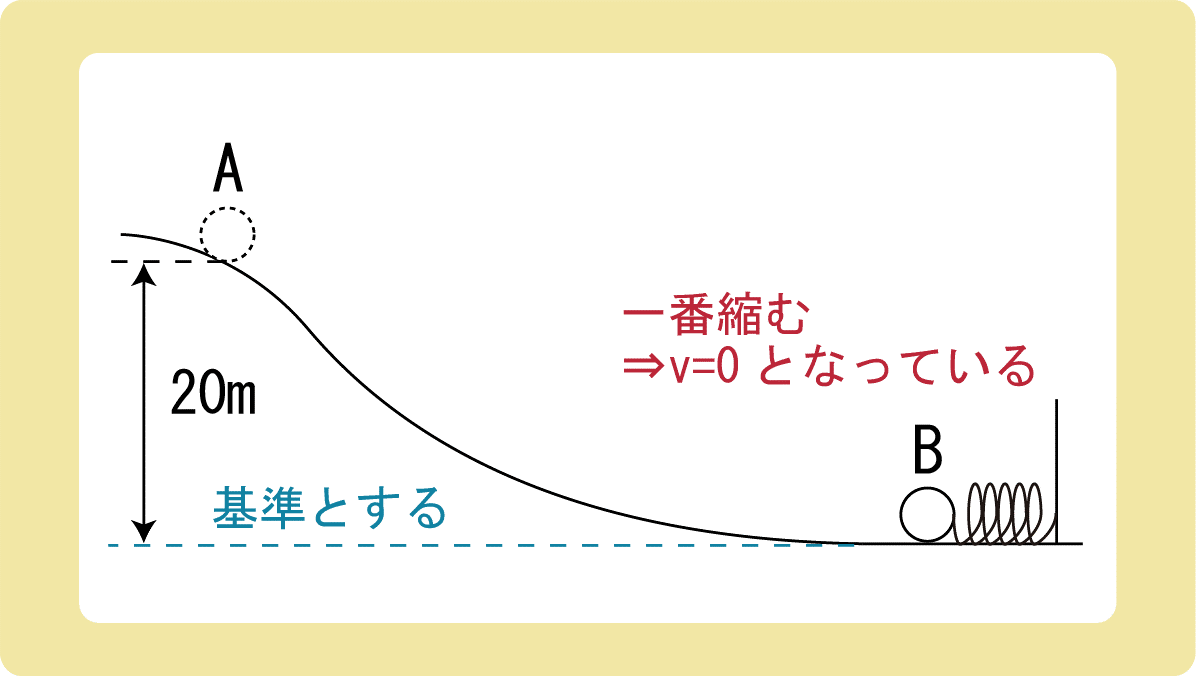
図のように、質量2.0kgの物体がなめらかな曲面上の点Aから静かに滑り始めた。物体が水平面におかれたバネ定数100N/mのバネを押し縮めるとき、バネは最大で何m縮むか。ただし、重力加速度の大きさを9.8m/s2とする。
例題2のバネver.です。
バネが出てきたときは、弾性力による位置エネルギー
$$\frac{1}{2}kx^2$$
を使うと考えましょう。
いつものように、一番低い位置のBを高さの基準とします。
例題2のように、物体は曲面上を滑ることによって、重力による位置エネルギーが運動エネルギーに変わります。
その後、物体がバネを押すことによって、運動エネルギーが弾性力による位置エネルギーに変化します。
力学的エネルギー保存の法則より
mgh=\frac{1}{2}kx^2\\
2.0×9.8×20=\frac{1}{2}×100×x^2\\
2.0×9.8×20=\frac{1}{2}×100×x^2\\
x^2=7.84\\
x=2.8$$
∴2.8m
力学的エネルギー保存の法則と摩擦力・摩擦熱
摩擦力がはたらく場合、物体のもつ力学的エネルギーは減少する。
$$μN×L$$
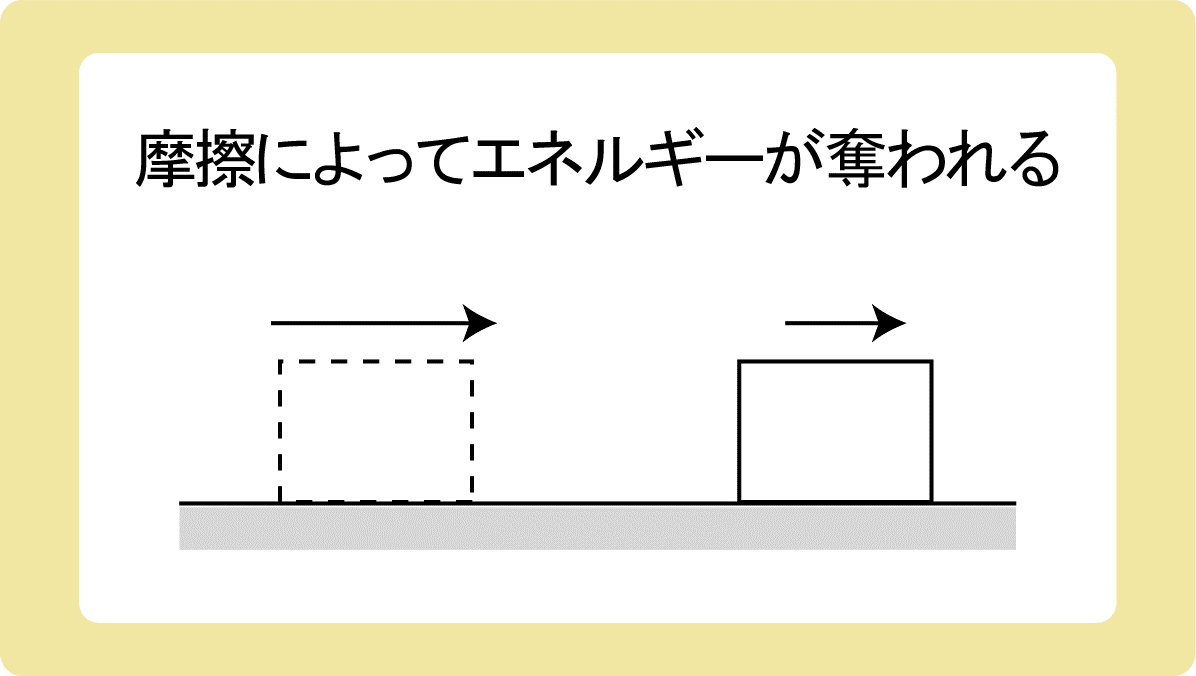
摩擦力がはたらく場合、物体の持つ力学的エネルギーは減少します。
摩擦のせいで力学的エネルギーは保存しなくなってしまうのですが、物体が失ったエネルギーと摩擦力が奪ったエネルギーの大きさは同じなので、広く全体でみるとエネルギーは保存していると考えることができます。
なお、摩擦力が奪ったエネルギーは摩擦熱として放出されます。
このとき、仕事の公式は\(W=Fs\)
摩擦力の公式は\(F=μN\)
なので、2つを合わせることにより、摩擦力が奪うエネルギーは
$$μN×L$$
となります。
摩擦がエネルギーを奪う場合、この式を使うことで問題を解くことになるでしょう。
例題
例題5
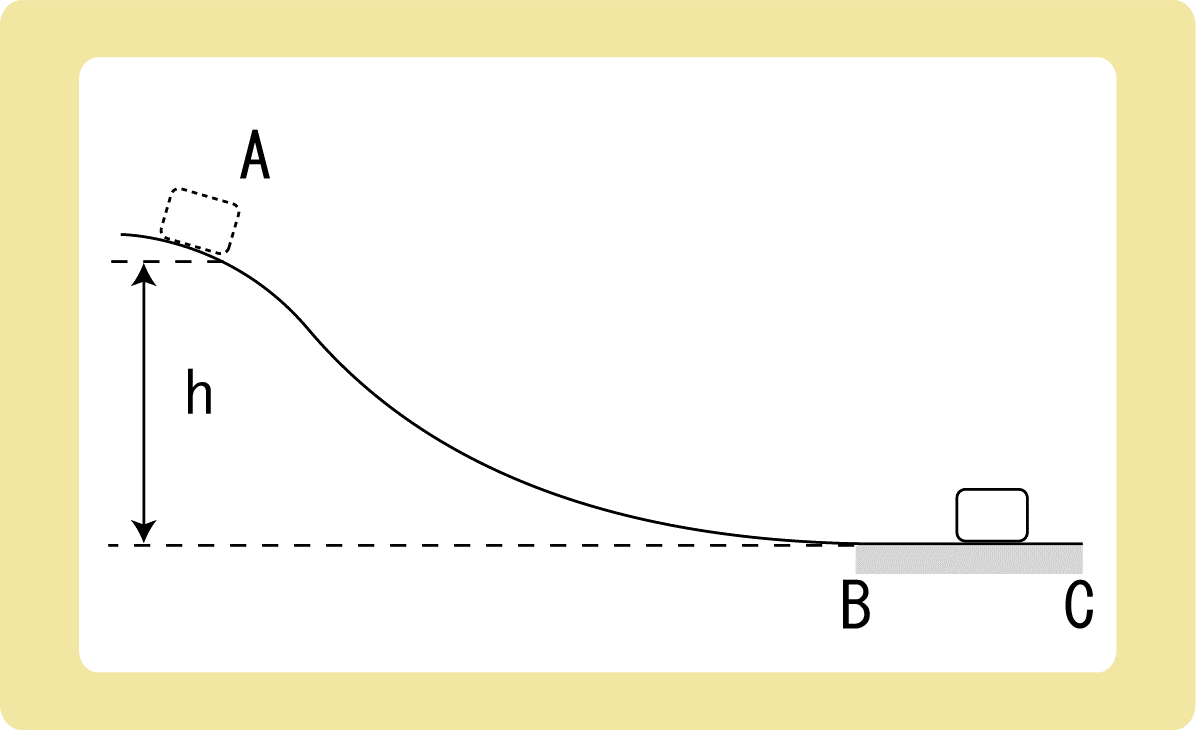
図のように、物体がなめらかな曲面上の点Aから静かに滑り始めた。物体があらい水平面に到達した後、あらい水平面BC上で物体は停止した。点Bから止まった位置までの距離は何mか。ただし、物体とあらい水平面との間の動摩擦力をμとする。
いつも通り、水平面BCを高さの基準とします。
物体の持っていた力学的エネルギーが全て摩擦力に奪われた(摩擦熱になった)と考えます。
つまり、
$$mgh+\frac{1}{2}mv^2=μNl$$
と、立式します。
もちろん、静かに滑り始めているので、初速度は0であり、
$$mgh=μNl$$
となります。
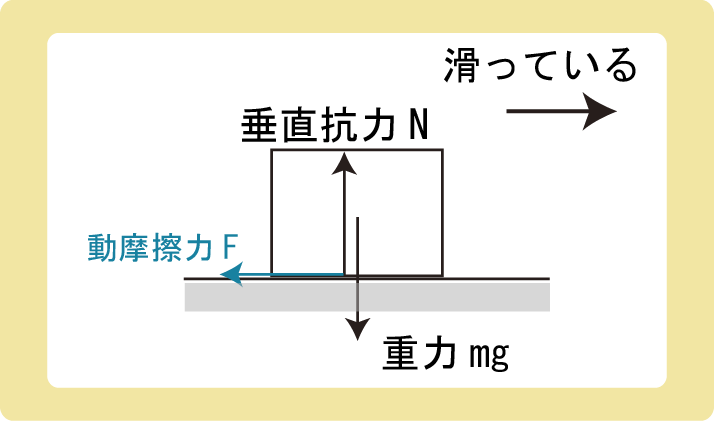
ここで、水平面上を滑っている物体にはたらく動摩擦力は\(F=μN\)より
$$F=μmg$$
となります。
これを代入すると、
$$mgh=μNl\\
mgh=μmgl\\
h=μl\\
l=\frac{h}{μ}$$
∴\(\frac{h}{μ}\)
となります。
まとめ
今回は力学的エネルギー保存の法則について、問題の解き方を中心に学びました。
物体がまっすぐではない運動をしているとき、力学的エネルギー保存の法則を使うと疑いましょう。
ポイントは、2つの状態の力学的エネルギーを比べることです。
また、摩擦がある場合でも力学的エネルギーを使うときがあります。
そのときは、力学的エネルギーの減少した量＝摩擦に奪われたエネルギー
と考えましょう。
力学的エネルギー保存は、物理全体を通して使っていく考え方・公式であるため、何度も読み直して復習することをオススメします。
今後、力学的エネルギー保存の法則が登場する度に、今回の内容を覚えているかどうか聞くことになるでしょう。
少し長くなりましたが、今回の解説はこれで終わります。
