・熱量とは
・比熱と熱容量とは
・比熱と熱容量の公式と使い方
鉄はすぐ温まりますが、水は全然温まらないですよね。
すぐ近くの金属を触ってみてください。最初はひんやりとしていますが、すぐに温かくなります。
コップの中でもなんでもいいので、水を触り続けてみてください。水は全然温まらず、こちらの手が先に冷えてしまいます。
今回は、物体を温めるのにどれくらいの熱が必要なのか、物体はどれくらい温まりやすいのかについて、わかりやすく簡単に解説をしていきます。
熱量とは
物体と物体の間で熱として移動するエネルギーの量のこと。
熱量とは、物体と物体の間で熱として移動するエネルギーの量のことです。記号はheat quantityのQを使い、単位は［J］となります。
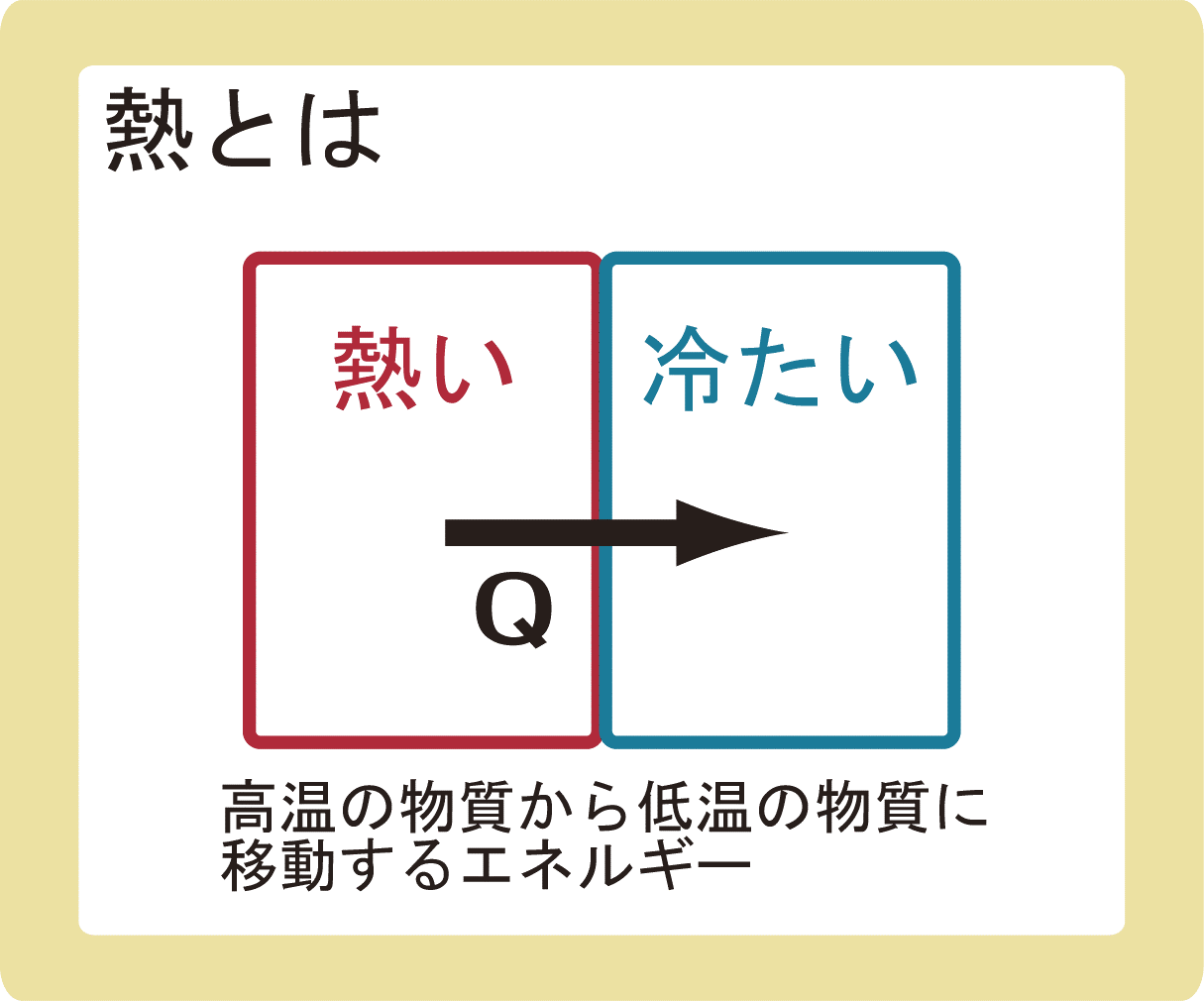
熱いものと冷たいものを接触させると、熱いものの温度は下がり、冷たいものの温度は上がります。
このとき、熱いものから冷たいものに移動したエネルギーのことを熱といい、その量を熱量と言います。
物理基礎や物理では、熱量Q［J］を使って様々な計算をしていきます。
熱容量とは
物体の温度を1K(1℃)上げるのに必要な熱量。
$$Q=CΔT$$
(Q：熱量［J］ ΔT：温度変化［K］)
熱容量とは、物体の温度を1K(1℃)上げるのに必要な熱量のことであり、記号はheat capacityのC、単位は［J/K］です。
熱容量が150J/Kの物体があるとすると、「この物体に150Jの熱を与えると、温度が1K(1℃)上がる」という意味になります。
もし2K(2℃)上げたいのであれば、300Jの熱を加えればよいでしょう。
従って、公式は\(Q=CΔT\)という単純な式になります。
Δ(デルタ)は変化を表します。
Tは絶対温度なのですが、ΔTになることで温度変化という意味になります。
なお、絶対温度とセルシウス温度の目盛りの幅は同じなので、「温度を1K上げる＝温度を1℃上げる」となります。
例えば「温度が20℃から25℃に変化した」場合は、どうせ絶対温度とセルシウス温度の目盛りの幅は同じなので、ΔT=5Kとして大丈夫です。
熱量と熱容量、名前は似ていますが意味は異なるので間違えて覚えないようにしましょう。
熱量がQ、熱容量はCです。
比熱とは
1gの物質の温度を1K(1℃)上げるのに必要な熱量。
$$C=mc$$
$$Q=mcΔT$$
(Q：熱量［J］ m：質量［g］ ΔT：温度変化［K］)
比熱とは、1gの物体の温度を1K(1℃)上げるのに必要な熱量のことです。
水は温まりにくい、鉄は温まりやすい等、物質によって温度の上がりやすさは決まっています。
1gあたりの物質の温まりやすさを比熱といい、記号cで表し、単位は［J/(g・K)］となります。
熱容量は大文字のCですが、比熱は小文字のc。
熱容量と比熱の違いは「1gあたりかどうか」という点です。
「1gあたりかどうか」という違いなので、公式も質量mがあるかないかの違いしかありません。
ある意味、1gあたりの熱容量が比熱であると言えるので、
$$\frac{C}{m}=c\\
C=mc$$
となります。
これを\(Q=CΔT\)に代入することで、
$$Q=mcΔT$$
という式を作ることができます。
色々な公式が出てきましたが、物理基礎の熱の範囲で一番使う式はQ=mcΔTです。
とりあえず、\(Q=mcΔT\)は覚えておきましょう。
また、熱容量や比熱は「温度を上げるために必要な熱量」なので、熱容量や比熱が大きいほど物体の温度は上がりにくくなります。
もしかしたら、こういう感覚が大事になってくるかもしれませんね。
例題
例題1
次の各問に答えなさい。
(1)1200Jの熱を加えると、物体の温度が300Kから320Kに変化した。物体の熱容量は何J/Kか。
(2)50gの水の温度を2℃上げるためには何Jの熱が必要か。ただし、水の比熱を4.2J/(g・K)とする。
例題2
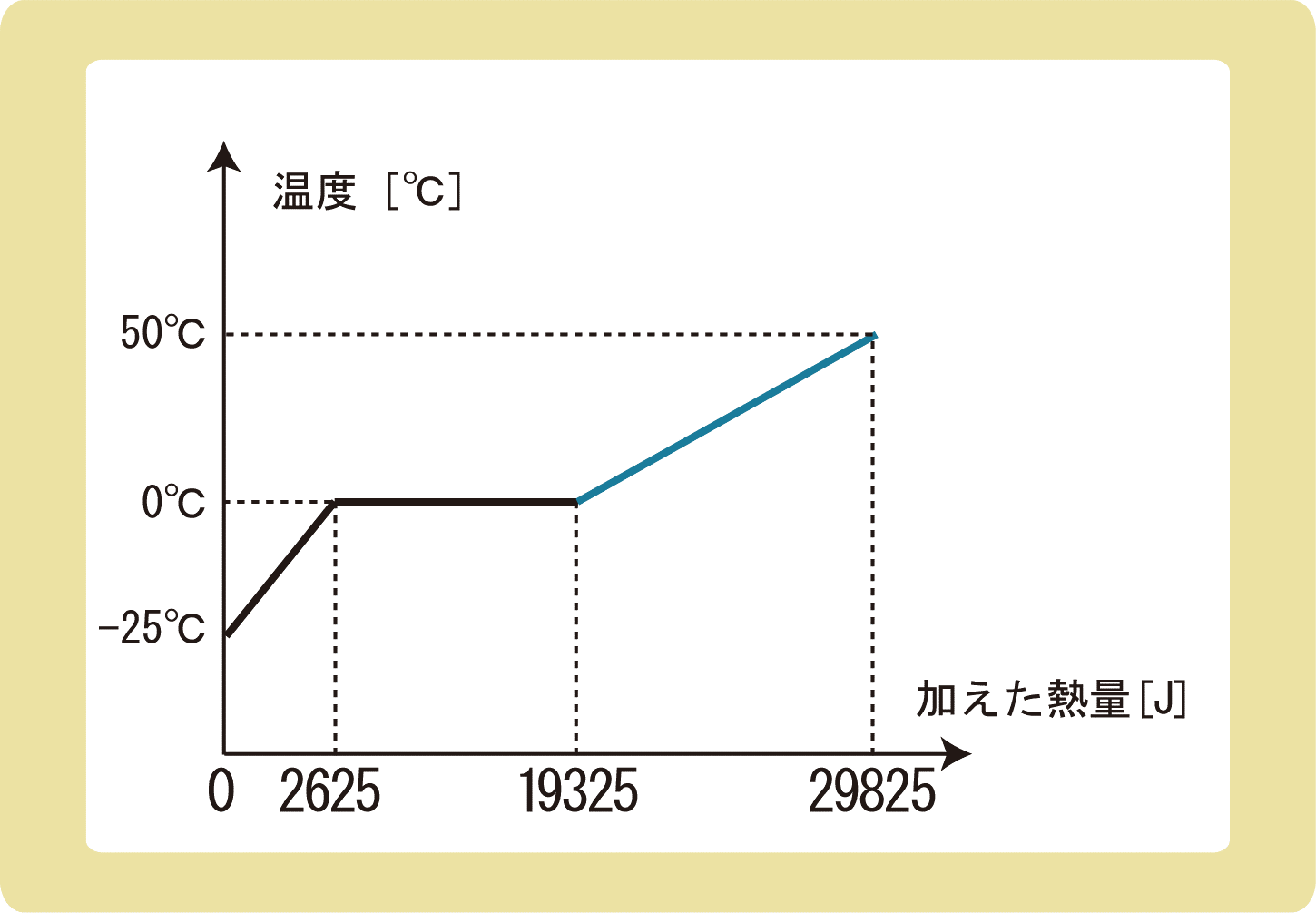
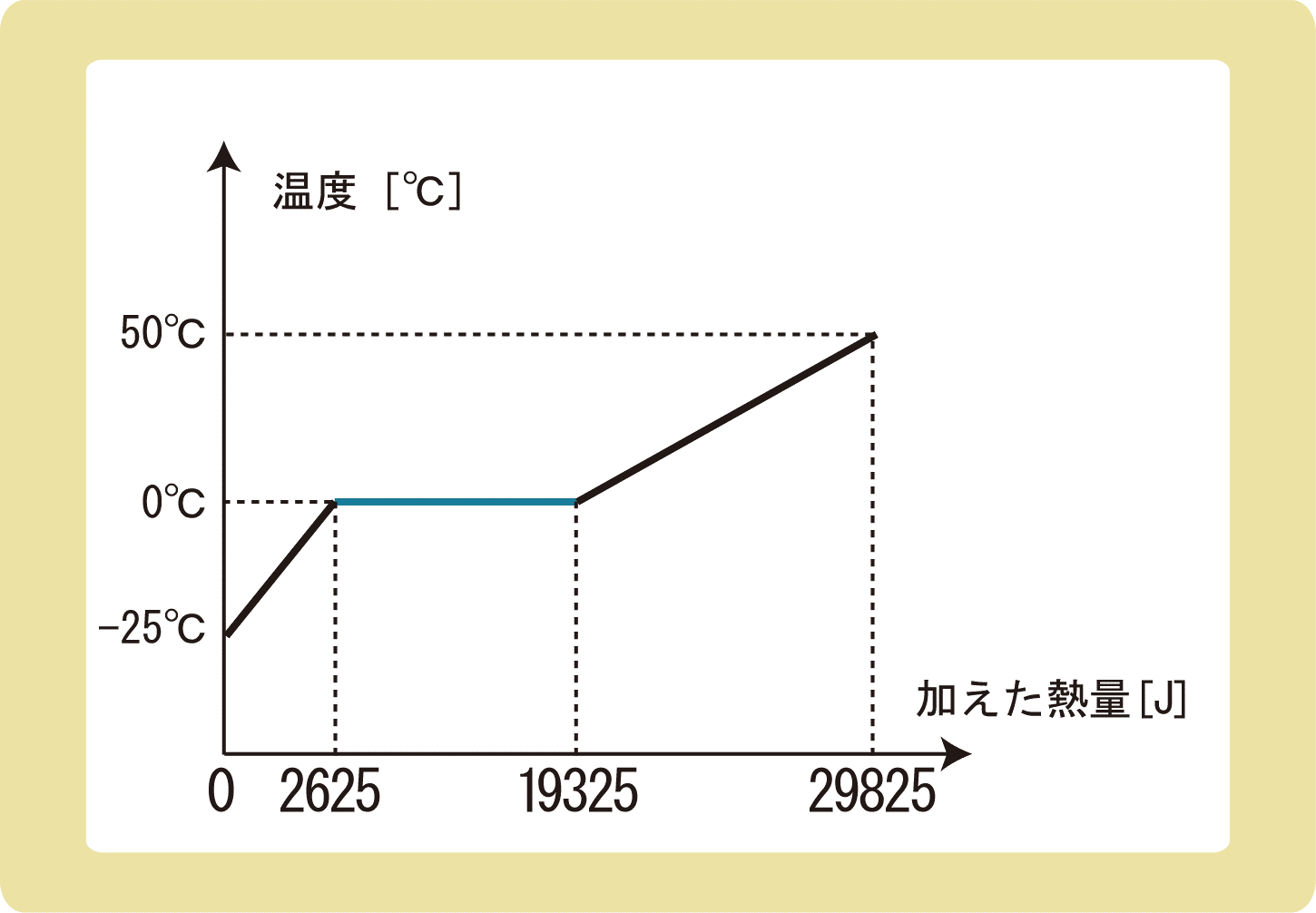
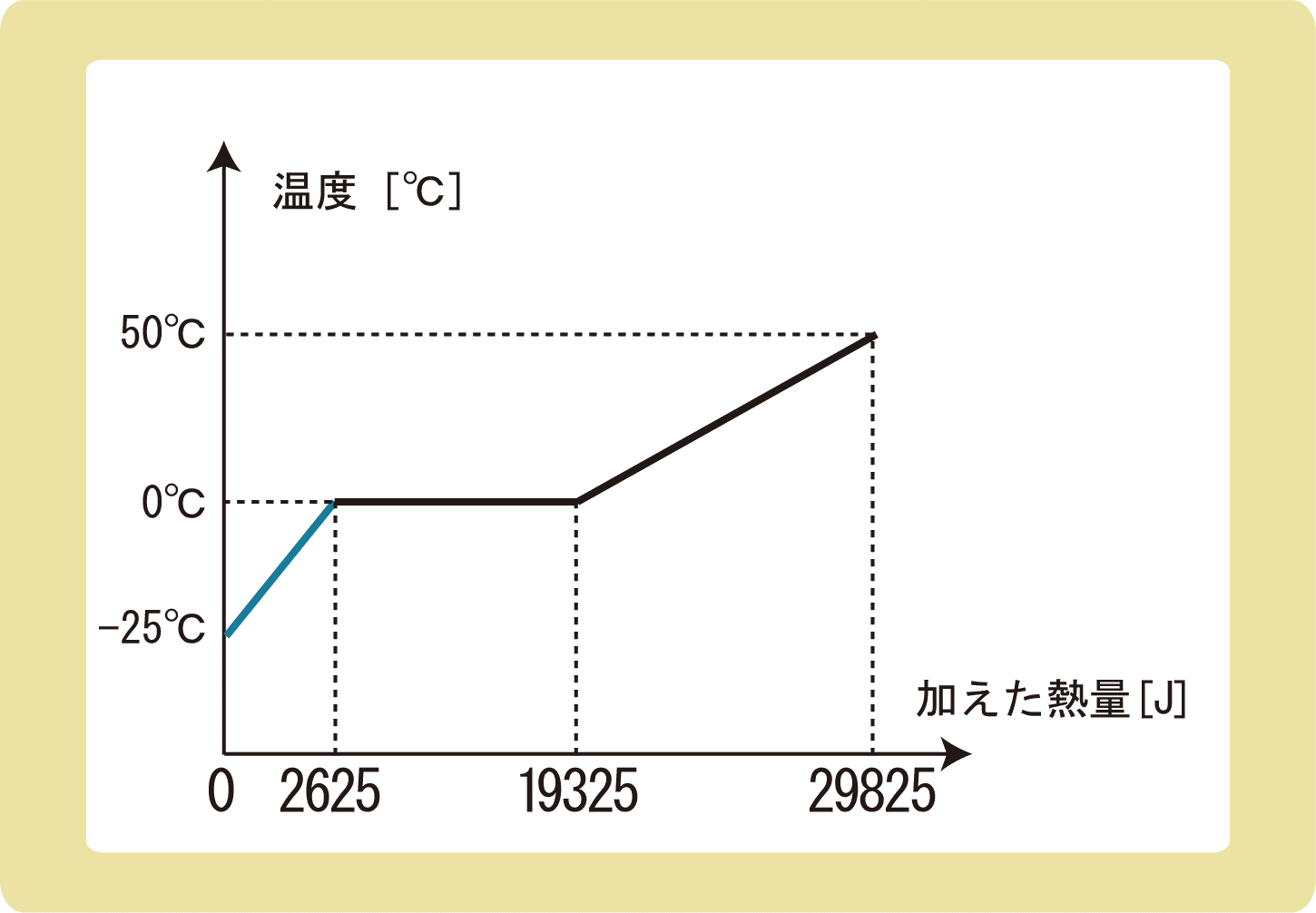
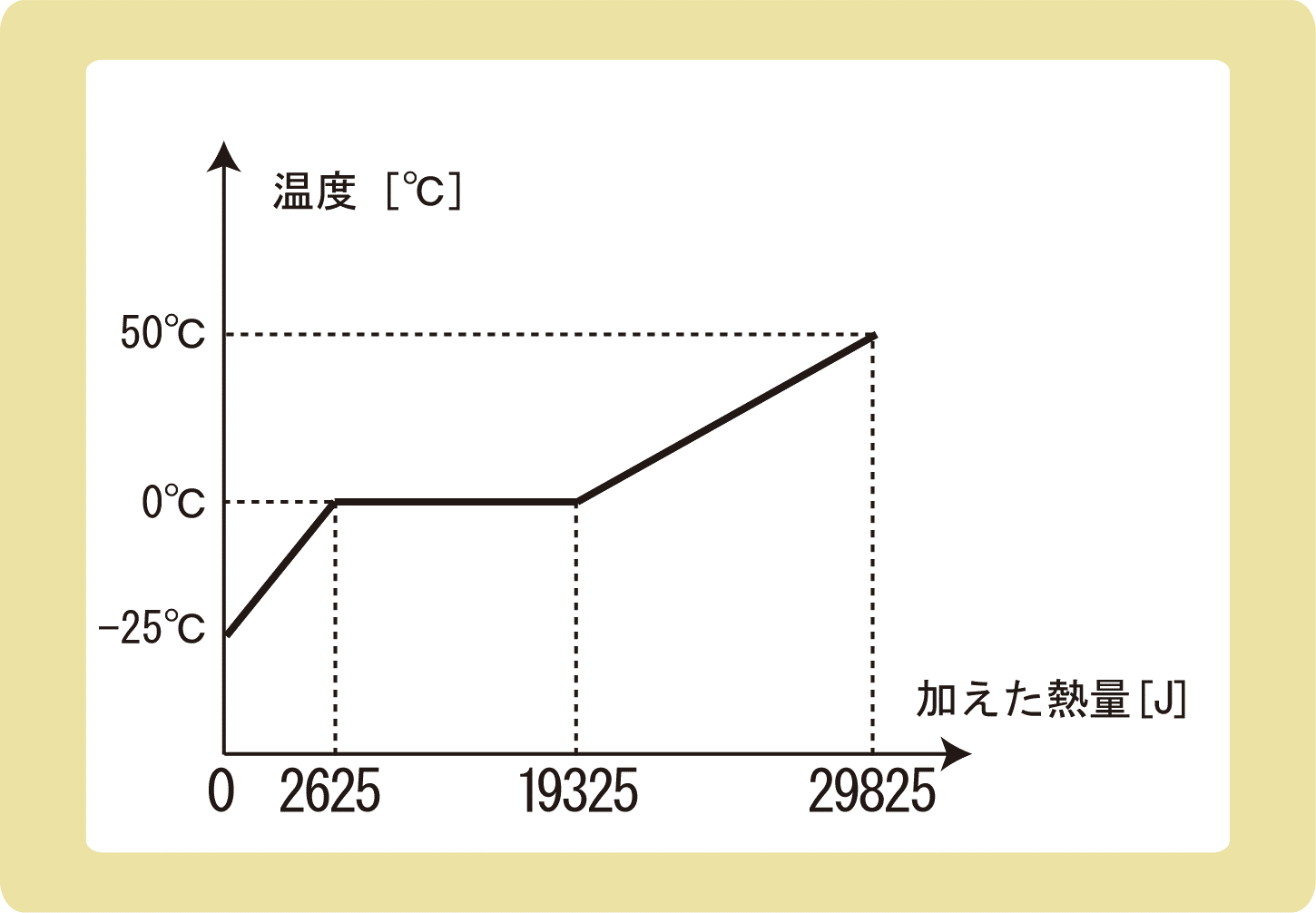
下図は、氷にゆっくりと熱を与え続けたときの、加えた熱量と温度の関係を表したグラフである。以下の問に答えなさい。ただし、水の比熱を4.2J/(g・K)とする。
(1)この氷の質量は何gか。
(2)この氷の融解熱は何J/gか。
(3)この氷の比熱は何J/(g・K)か。
氷が-25℃から0℃まで温められた後、水に変化します。
水に変化している間は温度が変わらないので、真横のグラフになっています。
比熱があるので\(Q=mcΔT\)
また、融解熱や蒸発熱が出てきているので\(Q=mL\)も使うと考えましょう。
氷の温度を-25℃から0℃に上げるために必要な熱量をQ1
氷を解かすために必要な熱量をQ2
水の温度を0℃から50℃に上げるために必要な熱量をQ3
と、区別します。
(1)氷の質量を直接求めることはできません。
「元々あった氷」と「解けた後の水」の質量は同じなので、氷ではなく水の質量を求めましょう。
氷の比熱や氷の融解熱は分かっていないので、水の比熱を使いましょう。
水が0℃から50℃に上がるためには
$$Q_3=29825-19325\\
Q_3=10500$$
の熱が必要です。
$$Q=mcΔT$$
より
$$10500=m×4.2×50\\
m=50$$
∴50g
(2) (1)で求めた氷の質量を使います。
融解熱を求めるためには\(Q=mL\)を使います。
$$Q_2=19325-2625\\
Q_2=16700$$
なので、
$$Q=mL\\
16700=50×L\\
L=334$$
∴334J/g
(3) (1)で求めた氷の質量を使います。
比熱が求めるためには
$$Q=mcΔT$$
を使いましょう。
$$Q_1=2625$$
なので、\(Q=mcΔT\)より
$$2625=50×c×25\\
c=2.1$$
∴2.1 J/(g・K)
まとめ
熱量がQ［J］、熱容量がC［J/K］、比熱がc［J/(g・K)］、温度変化がΔTです。
熱容量が登場しているときは\(Q=CΔT\)を使い、
比熱が登場しているときは\(Q=mcΔT\)を使います。
この式を使って計算するのは、今回の内容と次回の熱量保存の法則だけです。
問題の種類もあまり多くないので、簡単に理解できて点数も取りやすい内容であると思います。
