・熱量保存の法則とは
・熱量保存の法則の問題の計算方法
物理基礎の熱の分野で一番よく出題される問題が「熱量保存の法則」についての問題です。
保存とは、力学的エネルギー保存の法則のように「何かが一定で変わらない」という意味になります。
今回は、熱量保存の法則がどのような法則なのか、計算方法等についてわかりやすく簡単に解説をしていきます。
熱量保存の法則とは
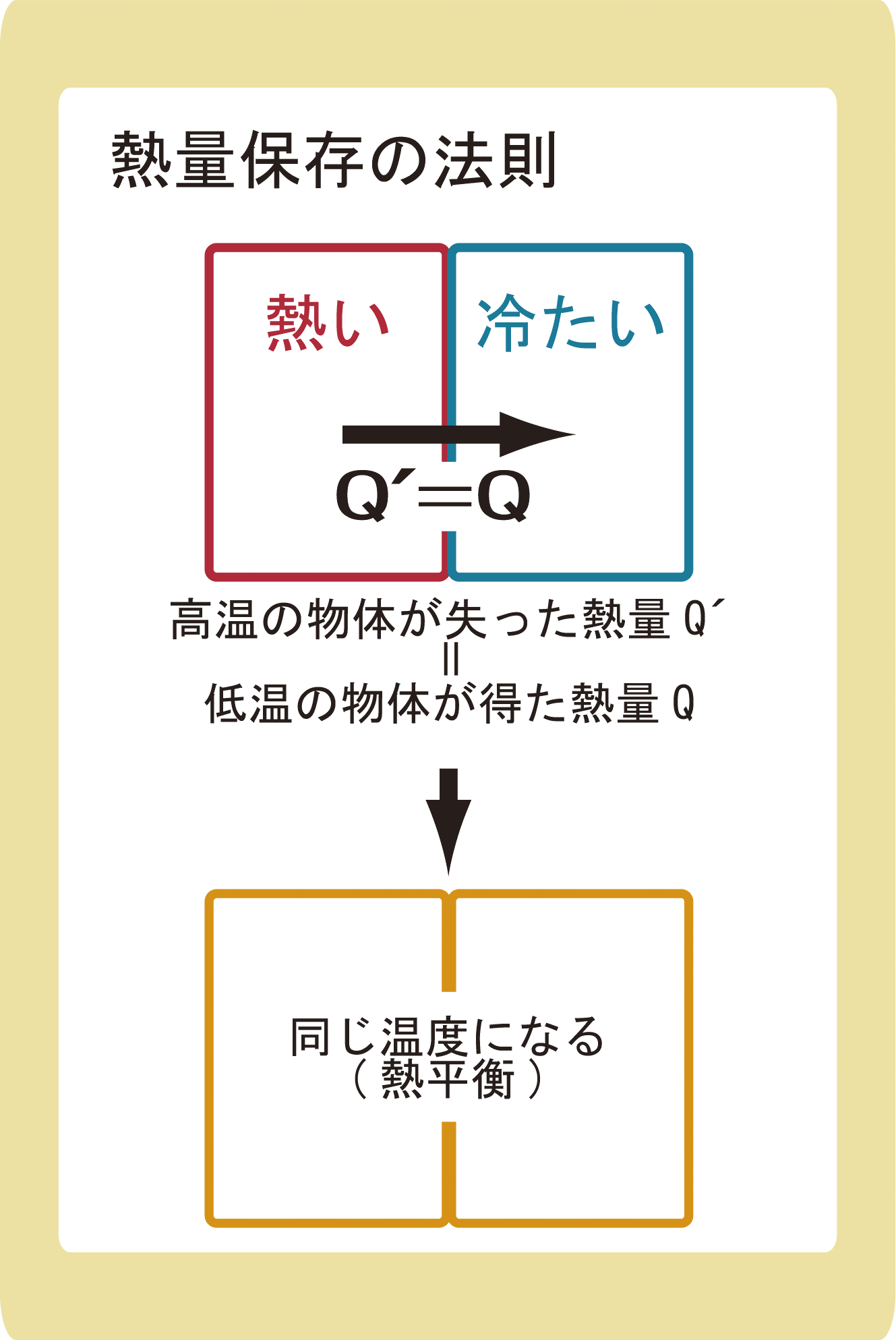
高温の物体が失った熱量＝低温の物体が得た熱量
熱量保存の法則とは、「高温の物体が失った熱量＝低温の物体が得た熱量」のことを言います。
熱いものと冷たいものを混ぜている問題が出たときは、熱量保存の法則を使って解きましょう。
熱いものと冷たいものを混ぜると、やがて同じ温度になります。(熱平衡(ねつへいこう)と言います)
このとき、高温の物体から低温の物体に熱が移動するのですが、熱が外部に逃げない場合、高温の物体から出たエネルギーと低温の物体が受け取ったエネルギーの大きさは等しくなります。
これが熱量保存の法則です。
熱量保存の法則では、高温の物体が失った熱量と低温の物体が得た熱量の計算式を立式する必要があります。
問題文に熱容量が書かれている場合は\(Q=CΔT\)
比熱が記載されている場合は\(Q=mcΔT\)
を使いましょう。どちらを使うかは問題によります。
温度変化ΔTに関してですが、
高温の物体が失った熱量＝低温の物体が得た熱量と立式する場合は、ΔTが必ずプラスになるように引き算をしてください。必ず、大きい方から小さ方を引きましょう。
では、例題に入ります。
例題
例題1
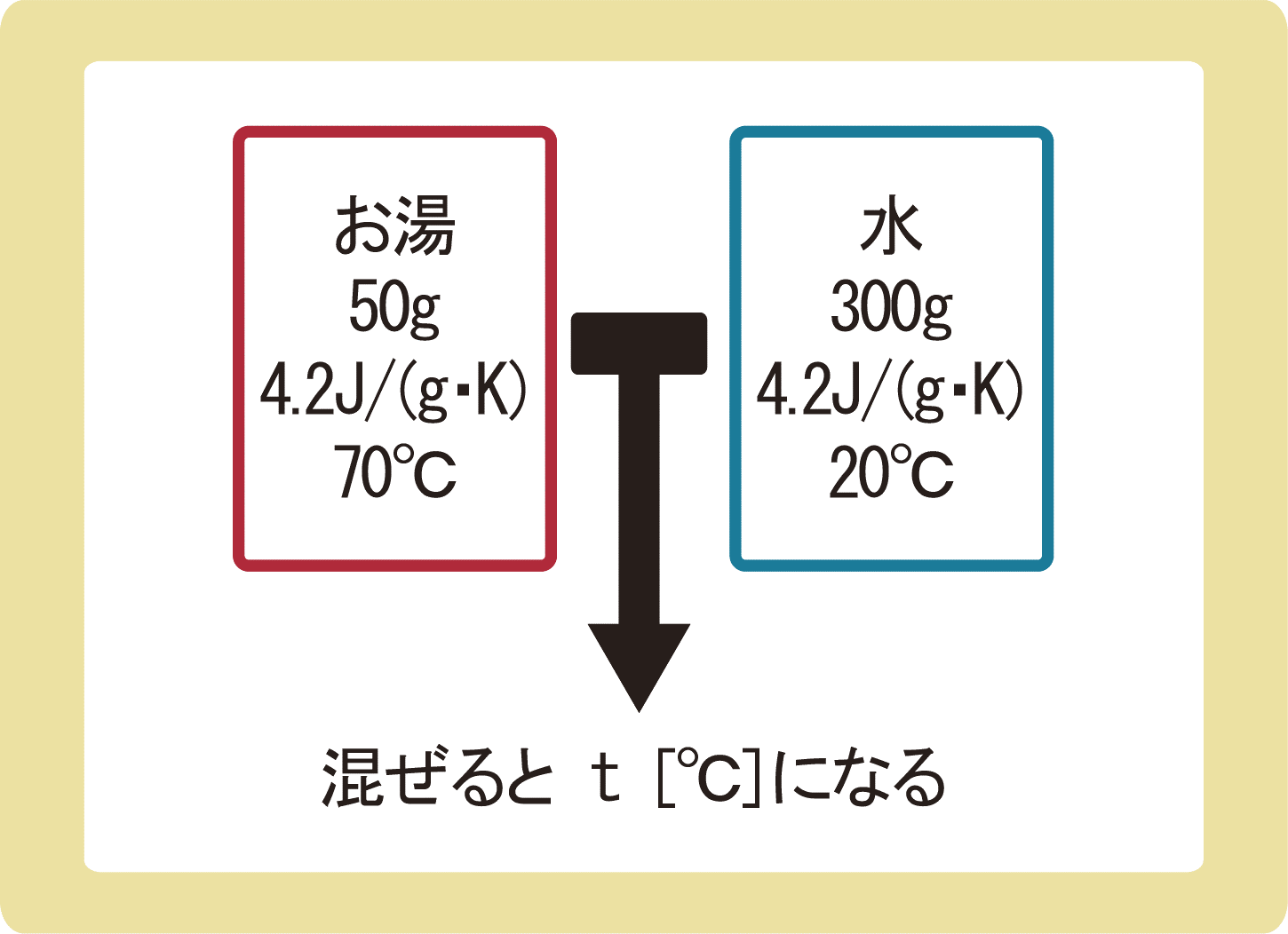
70℃の湯50gと20℃の水300gを混ぜると何℃になるか、有効数字2桁で答えなさい。ただし、水の比熱を4.2 J/(g・K)とし、熱は外部に逃げないものとする。
このような、熱いものと冷たいものを混ぜている問題では熱量保存の法則を使うと考えましょう。
まず、混ぜた後の温度(熱平衡温度)をt［℃］とします。
熱量保存の法則では、「高温の物体が失った熱量＝低温の物体が得た熱量」の式を作ればいいので、
高温のの物体が失った熱量Q’は
$$Q=mcΔT\\
Q’=50×4.2×(70-t)$$
低温の物体が得た熱量Qは
$$Q=mcΔT\\
Q=300×4.2×(t-20)$$
となり、
の式を作れるようになれば完璧です。
ここで、「高温の物体が失った熱量＝低温の物体が得た熱量」のように式を作る場合、ΔTは必ずプラスになるように引き算をしなければなりません。
ΔTは温度変化なので、70℃からt［℃］になった場合、温度は(70-t)［℃］変化したと考えます。
20℃の水と70℃のお湯を混ぜたということは、混ぜた後の温度は20～70℃の間にあるはずなので、引き算の順番は(70-t)と(t-20)となります。
ここを間違えると答えも変わってしまうので、間違えないように注意しましょう。
「高温の物体が失った熱量＝低温の物体が得た熱量」のように式を作る場合
ΔTはプラスになるように引き算をする。
では、計算をしていきます。
50×(70-t)= 300×(t-20)\\
1×(70-t)= 6×(t-20)\\
70-t= 6t-120\\
-7t= -190\\
t=27.14…$$<\div>∴27℃
例題2
80℃のアルミニウム50gを、20℃の水150gの中に入れると、全体の温度は何℃になるか。ただし、水の比熱を4.2J/(g・K)、アルミニウムの比熱を0.90 J/(g・K)とし、熱は外部に逃げないものとする。
例題3
図のように、断熱材に囲われている水熱量計に水を100g入れると全体の温度が22℃になった。この中に、90℃に熱した72.5gのアルミニウム製の物体を入れ、銅でできた棒で静かにかきまぜたところ、全体の温度が30℃になった。水の比熱を4.2J/(g・K)、銅の比熱を0.39J/(g・K)とし、銅の容器と銅の棒の合計の質量を150gとするとき、アルミニウムの比熱は何J/(g・K)となるか。
いつもより文章の長い問題ですが、物理の問題は文章が長くて当たり前なところがあるので、文章はしっかり読みましょう。
熱量保存の法則を使う問題に出てくる物体は2つのみとは限りません。
今回は、水・銅・アルミの3種類の物体で熱のやり取りが行われています。
水と銅が合わせて22℃であり、そこに90℃のアルミを入れ、全体が30℃になった。
ということは、冷たい方の物質が水と銅の2種類あることになります。
この図のようなイメージです。
アルミの失った熱量＝水が得た熱量＋銅が得た熱量
$$\color{red}{mcΔT}= \color{blue}{mcΔT} + \color{blue}{mcΔT} $$
このように式を作ることで計算をすることができます。
では、アルミニウムの比熱をcとして、式を作ってみましょう。
72.5×c×60=100×4.2×8+150×0.39×8 \\
72.5×c×6=10×4.2×8+15×0.39×8 \\
72.5×c×2=10×1.4×8+15×0.13×8 \\
72.5×c×1=10×0.7×8+15×0.13×4 \\
72.5×c=56+7.8 \\
72.5c=63.8\\
c=0.88$$
∴0.88J/(g・K)
計算は大変ですが、慣れていくしかありませんね。
まとめ
熱いものと冷たいものを混ぜると、やがて同じ温度になります。(熱平衡)
そのとき、「高温の物体が失った熱量＝低温の物体が得た熱量」となることを熱量保存の法則と言います。
正しい表現ではないのですが、高温の物体と低温の物体で
$$\color{red}{mcΔT}=\color{blue}{mcΔT}$$
と式を作って解きます。
比熱cではなく熱容量Cが出ている場合は、CΔTを使う。
熱いものと冷たいものを混ぜている問題は必ず熱量保存の法則を使うので、どの問題に使えばよいかは分かりやすいかと思います。
