理解力がない人の特徴は？その理由は？

理解力がない人の特徴は何でしょうか？その理由はあるのでしょうか？
また、物事をスムーズに理解できる人と理解できない人の違いは何でしょうか？

理解力がない人・理解できないことで困っている人には、「知識」と「論理的思考力」が足りていないという特徴があるように思えます。

いくつかの例を見ながら、理解力についての理解を深めていきましょう。

リーディングスキルテスト

リーディングスキルテストとは、文章の意味を正しく読み取ることができるか、読解力についてのテストです。
ネットサーフィンをしていると、半年に一度はリーディングスキルテストの問題と結果について見かけます。

例題1

以下の文を読みなさい。
Alexは男性にも女性にも使われる名前で、女性の名Alexandraの愛称であるが、男性の名Alexanderの愛称でもある。

この文脈において、以下の文中の空欄にあてはまる最も適当なものを選択肢のうちから1つ選びなさい。

Alexandraの愛称は（　　）である。

例題2

アミラーゼという酵素はグルコースがつながってできたデンプンを分解するが、同じグルコースからできていても、形が違うセルロースは分解できない。

この文脈において、以下の文中の空欄にあてはまる最も適当なものを選択肢のうちから1つ選びなさい。

セルロースは（　　）と形が違う。

これらの例題は、読めば誰でも理解できるような内容なのですが、例題1の正答率は中学生で53%、高校生で78%であり、例題2の正答率は中学生で9%、高校生で33%しかないという結果が出ています。

例題2は
①アミラーゼはデンプンを分解する
②デンプンはグルコースがつながってできる
③セルロースも同じグルコースからできるが、形が違う
④アミラーゼはセルロースを分解できない

という内容になっており、①〜④を読み取ることができれば、必ずこの文章を理解することができるはずです。
逆に、この文章がよく理解できない場合、①〜④のうちのどれかが理解できていないということになり、論理的に物事を理解する力が足りていないということになるでしょう。

また、元々セルロースとデンプンの違いを知っている場合、先程の文章を簡単に理解するが可能になります。
論理的思考力と知識のどちらかがあれば、これらの例題を理解することができるはずなのです。

なお、リーディングスキルテストについての細かい条件や方法については、以下の本を参照にしてください。

上記の問題以外にも様々な問題について扱っており、分類分けがしっかりされていて面白い本です。

論理的思考力の欠如が原因

論理思考パズル「天使と悪魔」

理解力がない人には、論理的思考力が低い特徴があります。

下の例題は、有名な論理思考パズルでもある「天使と悪魔」というものなのですが、最低限の論理的思考力があれば理解することができるはずです。

例題3

「嘘をつかない天使」、「嘘をつく悪魔」、「気分で嘘をつく人間」がいます。
しかし、外見からは誰が誰だかわかりません。
この３人をA、B、Cとします。

Aは「私は天使ではない」といい、

Bは「私は悪魔ではない」、

Cは「私は人間ではない」と話しました。

ABC、それぞれが何者かを答えてください。

パッと見るとAが人間であることが分かるため、あとは少し考えると、Bが悪魔、Cが天使と分かりますが、理解力がない人・理解が遅い人は、この問題を理解することができなかったり、理解するのが遅かったりします。

「論理的思考力」の欠如が理解できない・理解が遅いことの原因なのです。

最低限の「論理的思考力」があれば、天使と悪魔の論理パズルくらい、苦もなく理解できるはずですよね。

知識があれば理解も早まる

$$v=\frac{mg}{k}(1-e^{-\frac{k}{m}t})$$

縦軸を\(v\)、横軸を\(t\)として、このグラフを描きなさい。ただし、\(k、m、g\)は定数とし、\(e\)はネイピア数である。

と言われたとき、大学1年生程度の物理の知識を持っていれば「自由落下の終端速度」であると分かり、高校3年生程度の数学の知識を持っていれば「ただの指数関数のグラフ」であると分かるため、簡単に理解しグラフを描くことができます。
つまり、知識があればあるほど、理解が早くなるのです。

逆算して考えてみましょう。

\(v=\frac{mg}{k}(1-e^{-\frac{k}{m}t})\)の\(\frac{mg}{k}\)は係数であり、グラフ全体を\(\frac{mg}{k}\)倍しているだけです。
大雑把に考えるとグラフの形にはあまり影響しないため、無いもとして考えてみます。

$$v=1-e^{-\frac{k}{m}t}$$

1は、最終的にグラフを1ずつ増やしているだけなので、グラフの形を知る上では無いほうが簡単です。一旦消してみます。

$$v=-e^{-\frac{k}{m}t}$$

eにマイナスが付いてるのは面倒なため、プラスにしちゃいましょう。

$$v=e^{-\frac{k}{m}t}$$

\(\frac{k}{m}\)は定数です。グラフの傾きのようなものであり、無かったとしても大雑把な形は同じなので、外して考えます。

$$v=e^{-t}$$

マイナス乗はグラフが左右反転するという意味です、ややこしいので外します。

$$v=e^{t}$$

eはネイピア数といって、約2.7なので、3にしちゃいましょう。

$$v=3^{t}$$

そもそも\(v\)と\(t\)がややこしいので、yとxにします

$$y=3^{x}$$

ここまでくれば、高校2年生以上であれば全員簡単に描けるグラフになりますよね。
逆算はここまでにして、実際にグラフを描いてみましょう。

\(y=3^x\)は誰でも簡単に描けるような、普通の指数関数です。

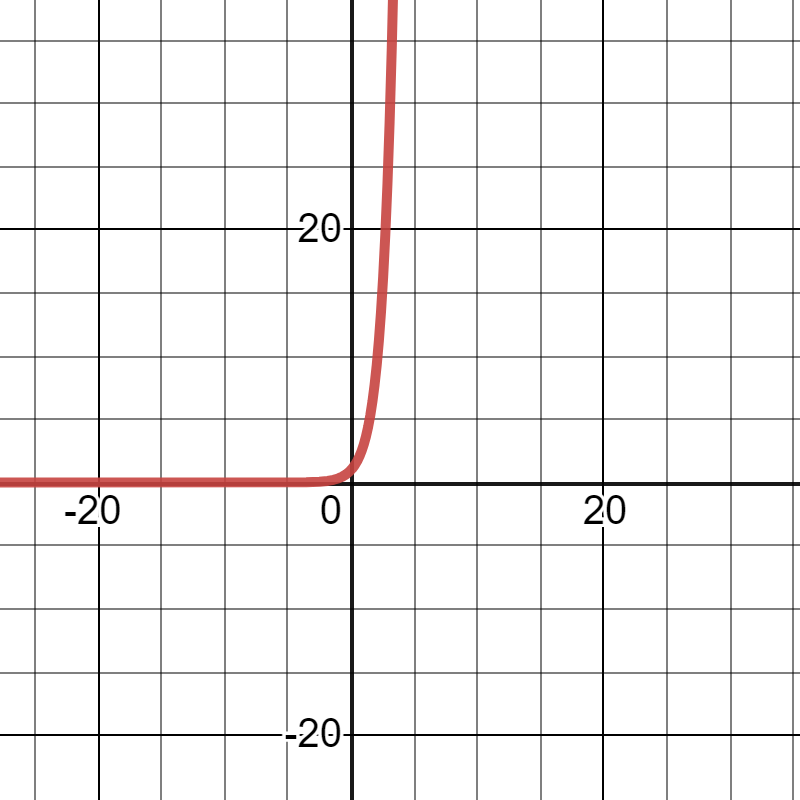
\(v=3^t\)にするため、縦軸と横軸を変えましょう。

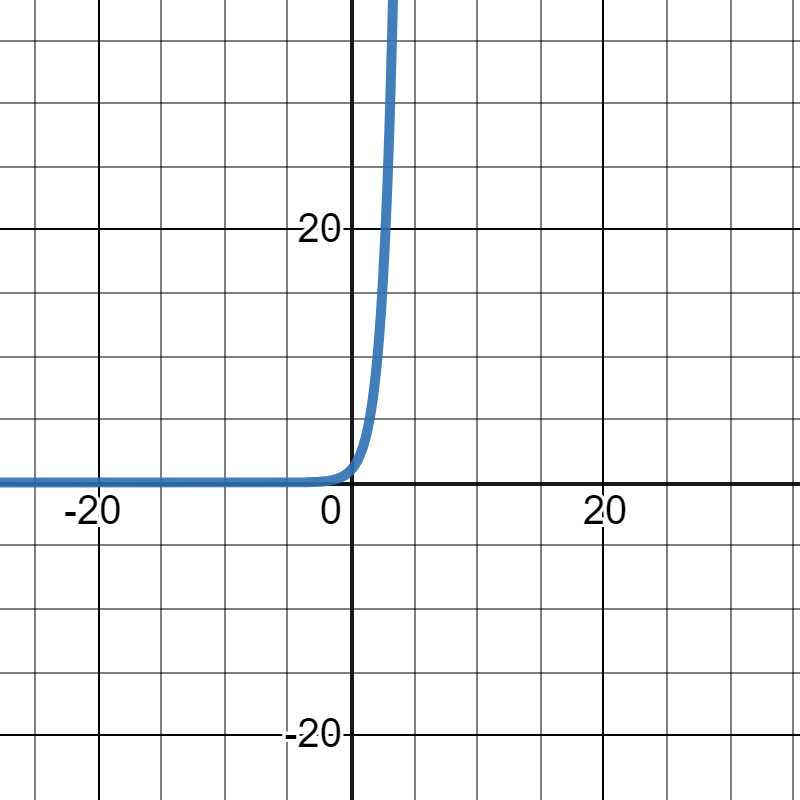
\(v=e^{t}\)にするため、3をeに戻します。
形は少しだけ変わりますが、ほぼ同じです。

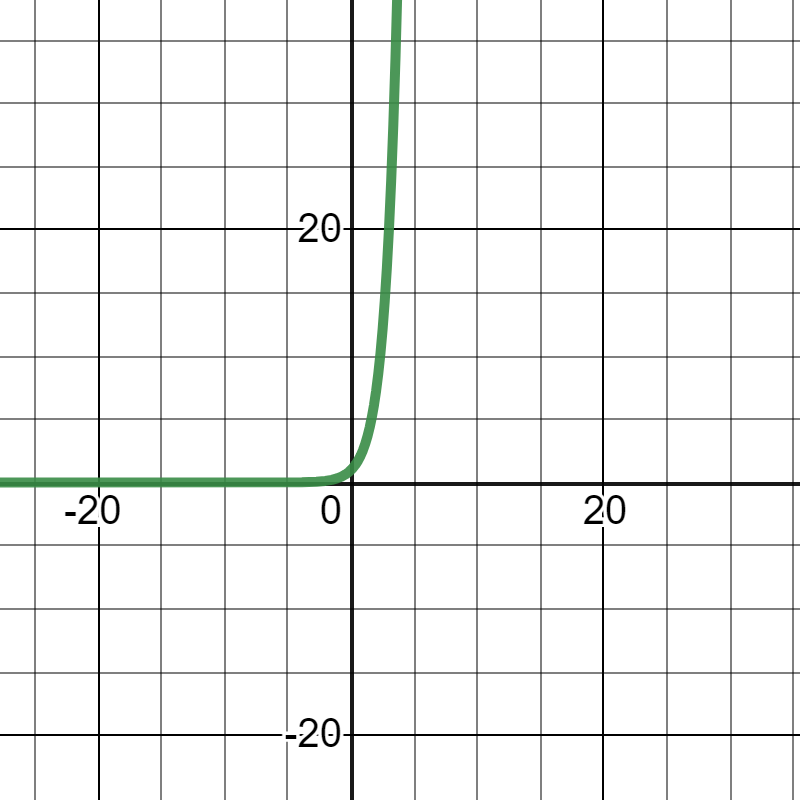
\(v=e^{-t}\)にすると、左右反転します。

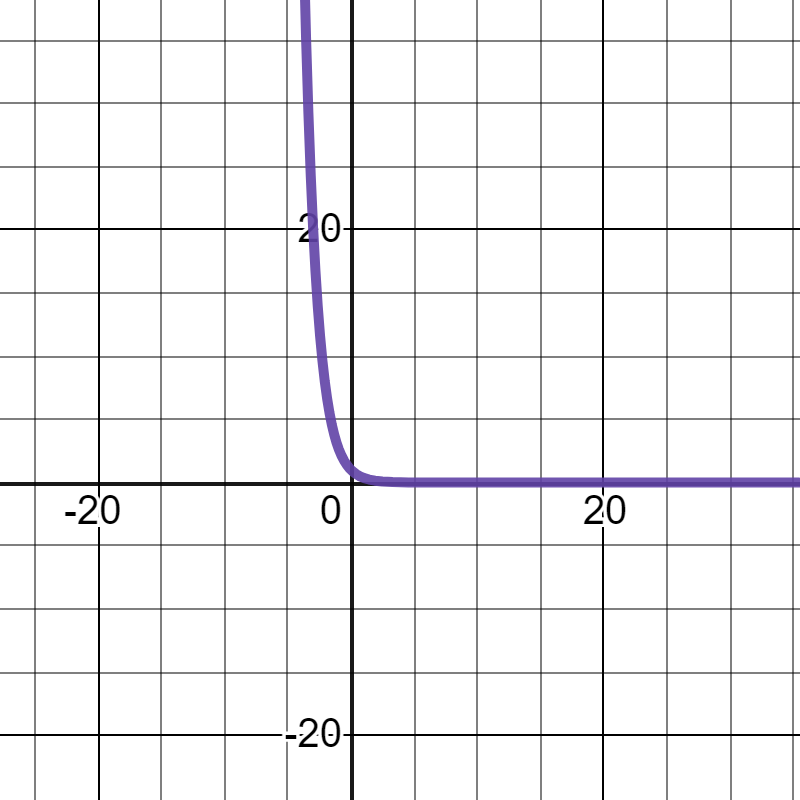
\(v=e^{-\frac{k}{m}t}\)にするため、定数をつけます。
定数は記号のままでもいいのですが、今回は\(k=0.3、m=0.5\)としてグラフを描きます。
少しグラフが横に大きくなります。

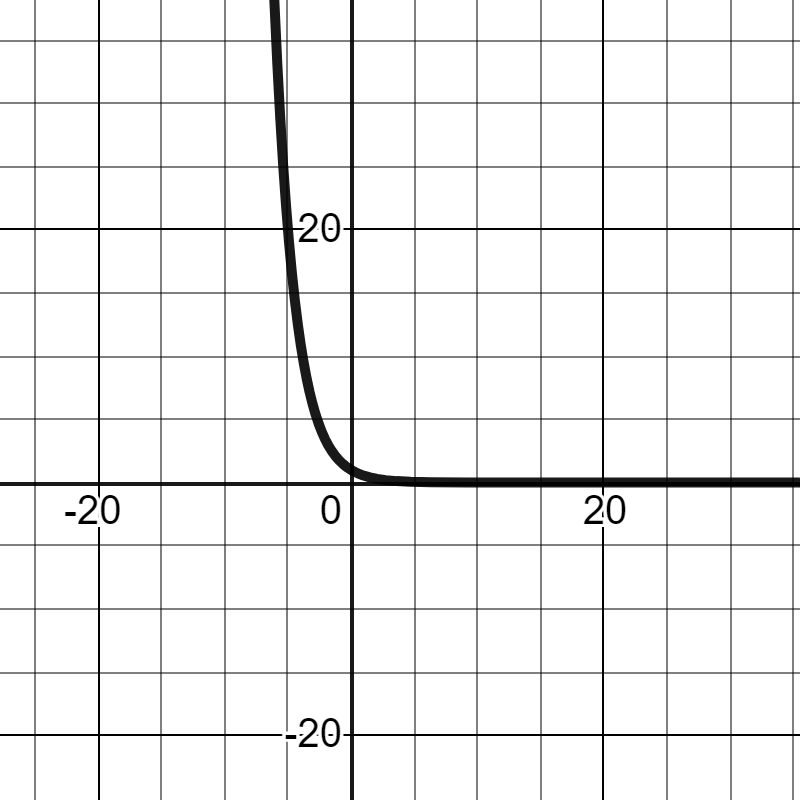
\(v=-e^{-\frac{k}{m}t}\)にするため、eにマイナスを付けます。
全体にマイナスが付くため、上下反転します。プラスマイナスが入れ替わる感じです。

\(v=1-e^{-\frac{k}{m}t}\)にするには、今のグラフに1を足します。
グラフは1ずつ上に移動します。

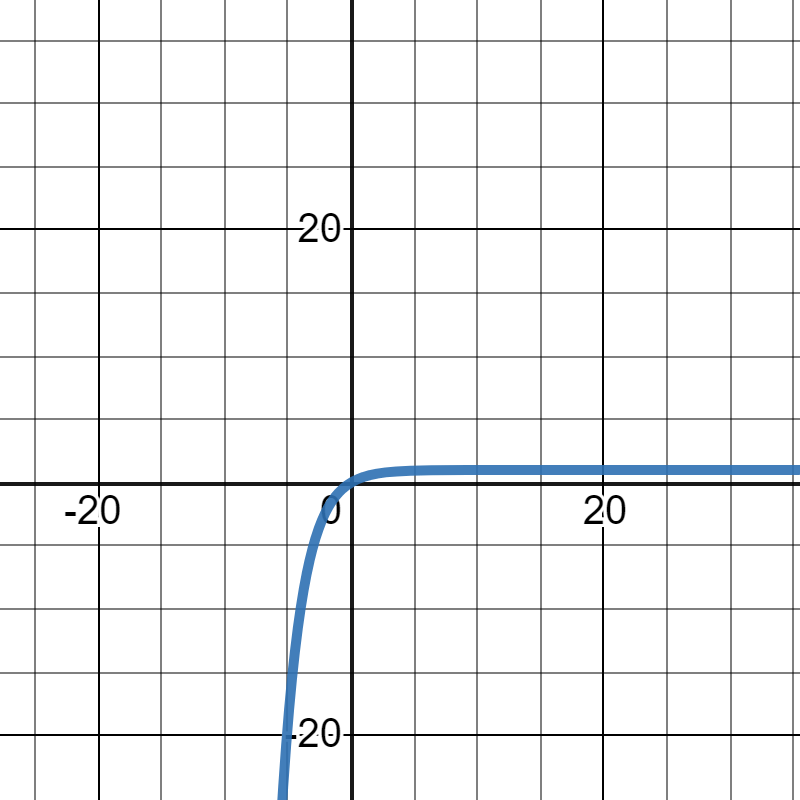
最後に、\(v=\frac{mg}{k}(1-e^{-\frac{k}{m}t})\)にするため、全体を\(\frac{mg}{k}\)倍にします。もちろん、\(g=9.8\)とします。

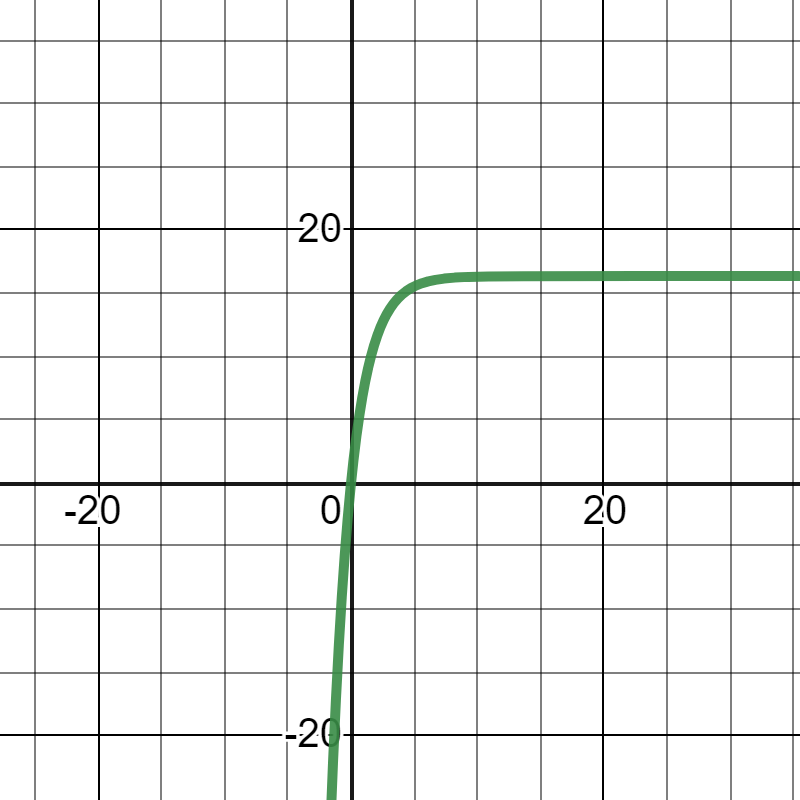
これで、\(v=\frac{mg}{k}(1-e^{-\frac{k}{m}t})\)のグラフを描くことができました。

グラフを説明するため、式を簡単な形に直してからグラフを描きましたが、知識があれば\(y=3^x\)まで遡らなくても、途中まで遡った段階で理解することができたはずです。

つまり、知識があることで途中の説明を省くことができ、理解するためのスピードが上がるのです。
知識がなければ、1つのことを説明するのに多くの前段階の知識から説明する必要があり、時間がかかってしまいます。

まとめ

理解力がない人には「論理的思考力」と「知識」が足りないという特徴があります。

「論理的思考力」と「知識」があれば理解することができる・理解が早まることは、上記の例から明らかですよね。

「論理的思考力」と「知識」は、どちらも短期間で鍛えることができないので、日々の積み重ねを大切にしましょう。