この記事で学べる内容
・鉛直面内での円運動について
前回の内容では、水平面上での円運動について例題として解きました。
ジェットコースターや振り子など、鉛直面で円運動をする問題も頻出です。
今回は、鉛直面での円運動についての問題を解きながら、わかりやすく簡単に解説していきます。
例題 鉛直面内での円運動と張力
例題1
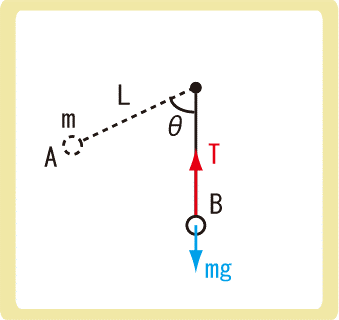
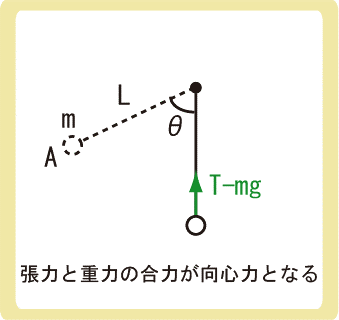
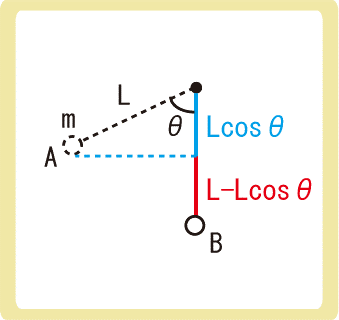
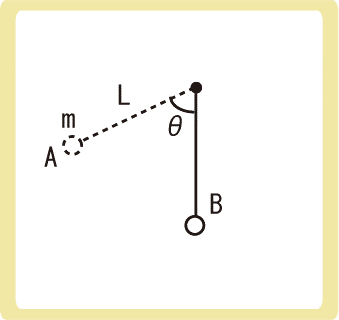
下図のように、長さLの糸に繋がられた質量mの物体を、点Aで静かに離した。物体が点Bを通過したとき、物体にはたらく張力の大きさを求めなさい。ただし、重力加速度の大きさをgとする。
例題2 鉛直面での円運動と垂直抗力
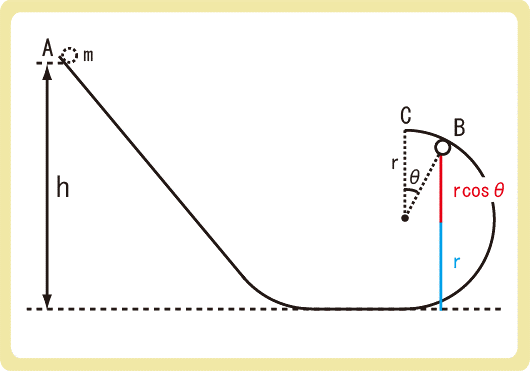
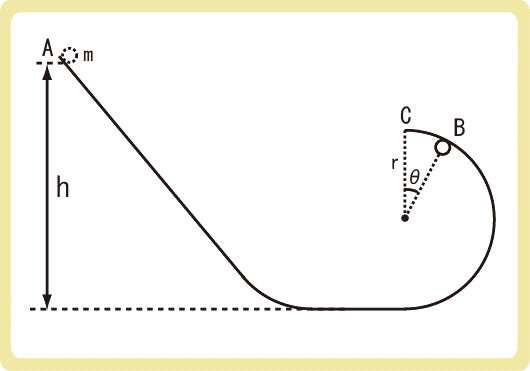
下図のように、高さhの点Aから質量mの物体を静かに転がしたところ、円形rの曲面内で円運動をした。重力加速度の大きさをgとするとき、以下の各問に答えなさい。
(1)点Bにおける物体の速さを求めなさい。
(2)物体が点Cまで円運動をするための、点Aの高さhの条件をrで表しなさい。
まとめ
鉛直面での円運動ではエネルギー保存の法則を使ってvを求め、向心力の式に代入するパターンばかりです。
物理基礎の問題をしっかり復習し、エネルギー保存の法則の問題に慣れたあと、鉛直面での円運動の問題をどんどん解いていきましょう。