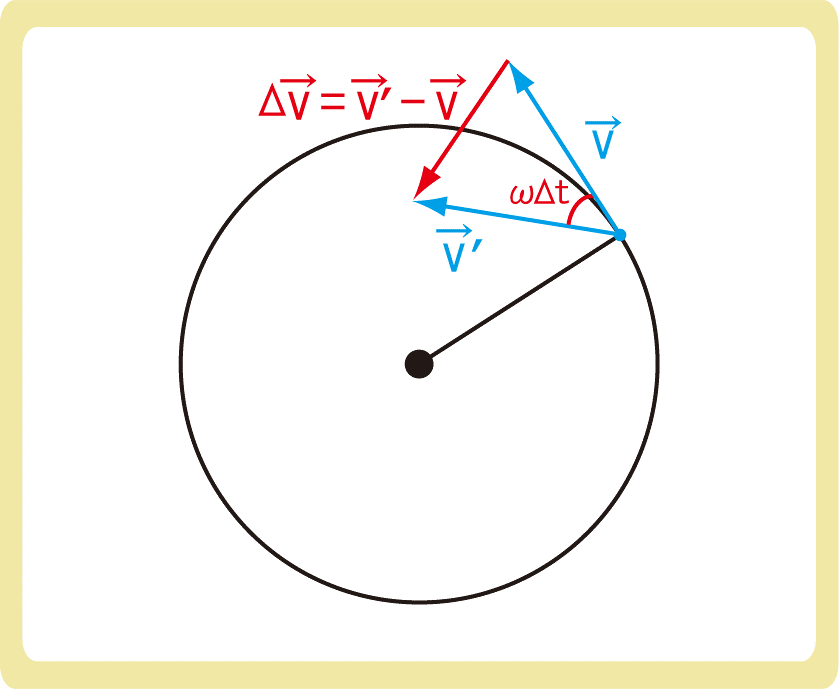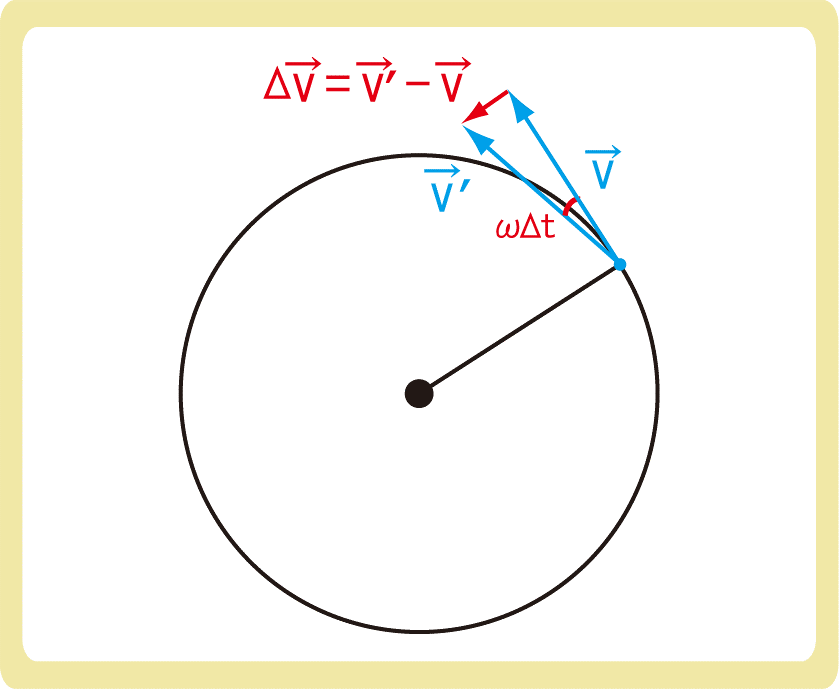・向心力とは
・向心力の式の導出
円運動では、速度の向きが常に変化しています。
速度の向きや大きさが変化するためには、物体に何かしらの力を加える必要があります。
今回は、円運動している物体にはたらく向心力について、わかりやすく簡単に解説をしていきます。
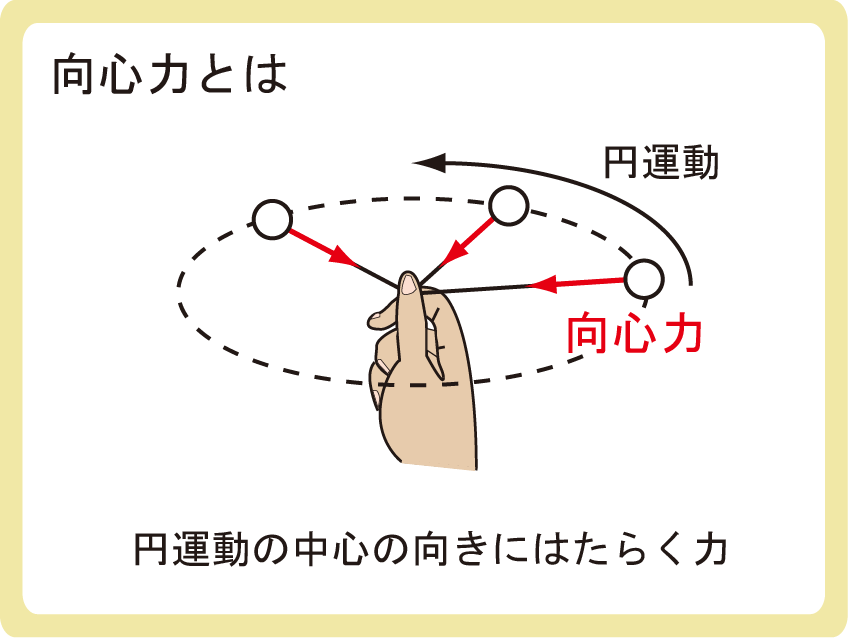
向心力とは
円運動の中心の向きにはたらく力
$$F=m\frac{v^2}{r}\\
F=mrω^2$$
向心力とは、円運動の中心の向きにはたらく力のことです。
円運動では、常に速度の向きが変化しています。
物体に何かしらの力が働いていないと物体の速度の向きは変化しません。上図のように、糸に繋がれた物体を水平に回すとき、物体は円運動の中心の方向に力を受けます。
ここで注意したいのは、向心力という力があるのではなく、円運動の中心の向きにはたらく力のことを向心力と呼ぶということです。
張力や弾性力など、様々な力が向心力としてはたらく場合があります。向心力は張力や弾性力、垂直抗力やその分力や合力かもしれないのです。
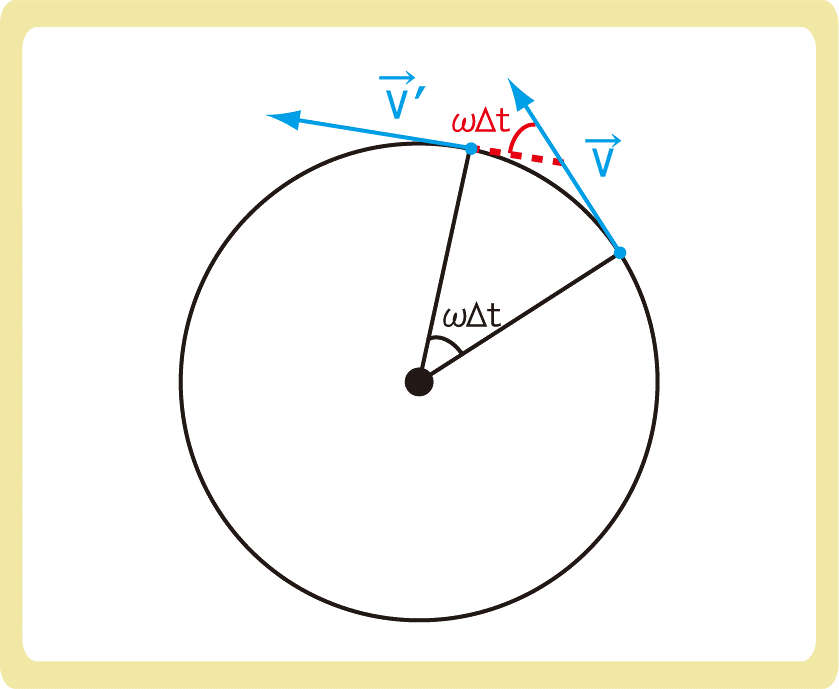
半径rの円周上を、角速度ωで等速円運動している物体を考えましょう。
時間Δtで物体がωΔtだけ回転したとき、物体の速度が\(\vec{v}\)から\(\vec{v}’\)に変化したとします。
このとき、2つのベクトル\(\vec{v}\)と\(\vec{v}’\)の始点を合わせると、2つのベクトルのなす角もωΔtになり、この2つのベクトルの引き算\(\vec{v}’-\vec{v}\)が速度の変化といえます。
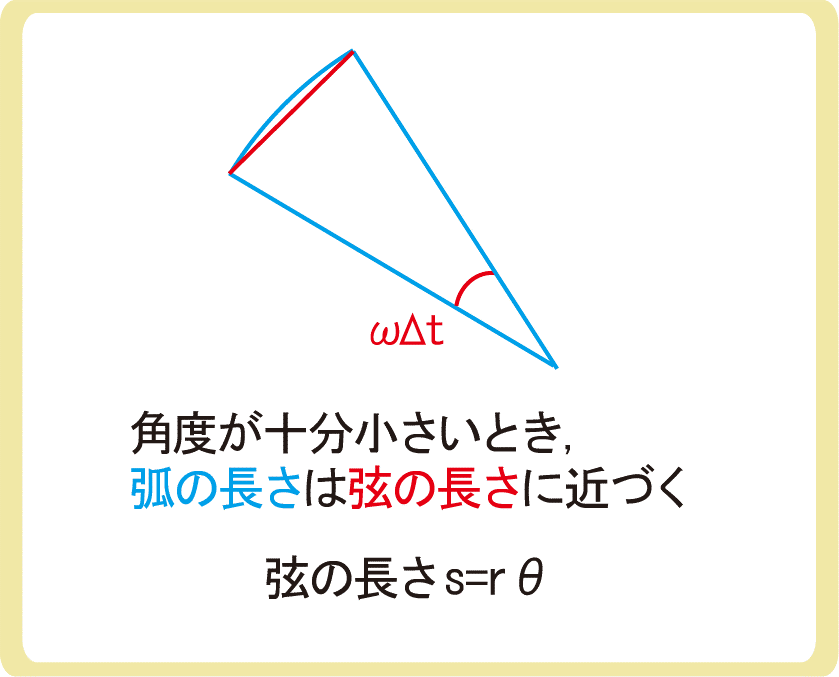
Δtが十分に小さいとき、弧の長さは弦の長さに近づくため、弧の長さを求める式である\(s=rθ\)より、\(|\vec{v}’-\vec{v}|=|\vec{v}|ωΔt\)となり、
$$|\vec{v}’-\vec{v}|=|\vec{v}|ωΔt\\
Δv=vωΔt \\
\frac{Δv}{Δt}=vω\\
a=vω$$
となります。あとは、\(v=rω\)を使って、
$$a=rω^2\\
a=\frac{v^2}{r}$$
となり、運動方程式\(ma=F\)より、
$$F=mrω^2\\
F=m\frac{v^2}{r}$$
と式を導出することができます。
円運動の公式まとめ
$$ω=\frac{θ}{t}$$
$$v=rω$$
$$T=\frac{2πr}{v}\\
T=\frac{2π}{ω}$$
$$n=\frac{1}{T}$$
$$F=m\frac{v^2}{r}\\
F=mrω^2$$
ω：角速度［rad/s］
\(v\)：速度［m/s］
r：半径［m］
T：周期［s］
n：回転数［s-1］
ちょっと多いですが、向心力を含めて上記が円運動の公式になります。大切なのは、
$$v=rω$$
$$T=\frac{2πr}{v}\\
T=\frac{2π}{ω}$$
$$F=m\frac{v^2}{r}\\
F=mrω^2$$
です。
これらの式を使って、円運動の問題を解いていきましょう。
例題
例題1
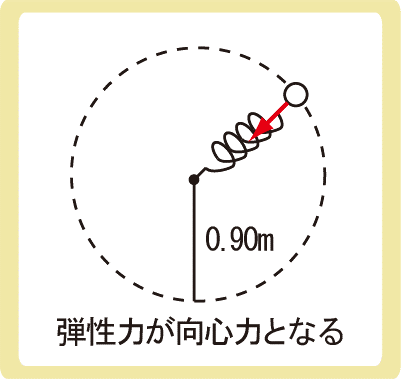
自然の長さが0.50m、ばね定数が10N/mのばねの一端を固定し、もう一端に質量0.10kgの物体を繋げて水平に円運動をさせたところ、ばねの長さが0.90mになった。この物体の速さを求めなさい。
まずは図を描いてみましょう。
ばねに繋がられた物体が円運動している図を描きます。
ばねの長さが0.90mになったということは、円運動の半径が0.90mということですね。
円運動することでバネが伸びているため、バネが元の長さに戻ろうとする弾性力がはたらきます。
この弾性力が円の中心を向いているので、今回の向心力は弾性力になります。
つまり、弾性力＝向心力と式を立てましょう。
$$kx=m\frac{v^2}{r}\\
10×0.40=0.10×\frac{v^2}{0.90}\\
v^2=\frac{10×0.40×0.90}{0.10}\\
v^2=36\\
v=6.0$$
xはバネの伸びた長さなので、もちろん0.40mですね。
∴6.0 m/s
例題2
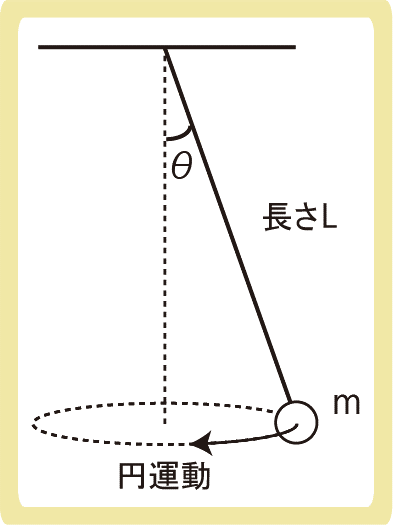
長さLの糸の一端を固定し、他端に質量ｍの物体をつるし、円錐振り子として等速円運動させた。糸が鉛直線となす角θが一定であるとき、この物体の周期を求めなさい。ただし、重力加速度の大きさをgとする。
周期を求めるためには、\(T=\frac{2πr}{v}\)か\(T=\frac{2π}{ω}\)を使います。2πは定数なので、ωかvが分かると周期Tが分かります。
この問題では、ωとvの両方を求めることができるのですが、今回はωを求めていきましょう。
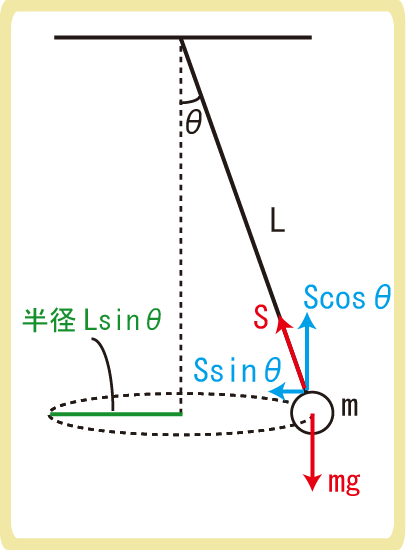
まずは力を図示します。上図の赤色の力が物体にはたらく力です。
重力はmg、張力はTにしてしまうと周期Tと被ってしまうので、Sにしておきましょう。
今回は水平方向に物体が運動しているので、上図の青い力のように、水平方向と鉛直方向に張力Sを分解します。
この物体は、鉛直方向には運動していないため、鉛直方向では力がつりあっているため
$$Scosθ=mg…①$$
と式を作ることができます。
水平方向では物体は円運動をしているため、何かしらの向心力がはたらいていると考えます。
今回は、張力Sの水平成分が向心力であることと、円運動の半径がLsinθになることから
$$mrω^2=Ssinθ\\
mLsinθ×ω^2=Ssinθ\\
mLω^2=S…②$$
となります。②のSを①に代入し、
$$ mLω^2×cosθ=mg\\
ω^2=\frac{g}{Lcosθ}\\
ω=\sqrt{\frac{g}{Lcosθ}}$$
とωを求めることができました。あとは\(T=\frac{2π}{ω}\)を使うと、
$$T=\frac{2π}{ω}\\
T=2π\sqrt{\frac{Lcosθ}{g}}$$
となります。
∴\(2π\sqrt{\frac{Lcosθ}{g}}\)
まとめ
向心力とは、円運動の中心の向きにはたらく力のことです。
物体が円運動しているとき、必ず円運動の中心方向に何かしらの力がはたらいていて、その力のことを向心力といいます。
あくまでも、円運動の中心を向いている力のことを向心力と呼ぶだけであり、向心力という力があるわけではありません。円運動の中心を向く力は弾性力だったり、垂直抗力や張力の分力だったりします。
向心力の大きさは、運動方程式より
$$F=m\frac{v^2}{r}\\
F=mrω^2$$
と表されます。この式を覚えておかないと問題は何も解けないので、問題を解きつつ覚えておきましょう。
