・単振動とは
・単振動と微分
・単振動の公式導出
物理基礎でも勉強した波動のような、周期的な運動を詳しく学ぶために、同じく周期的な運動である単振動について勉強します。
単振動は大学入試にもよく出題される内容であり、理解しておくと点数に繋がるため、しっかり勉強しておきましょう。
今回は、単振動とは何かについて、わかりやすく簡単に解説していきます。
単振動とは
直線上を往復する運動
等速円運動を回転面の真横から見たときの動き
$$x=Asinωt\\
v=Aωcosωt\\
a=-Aω^2sinωt\\
a=-ω^2x$$
単振動とは、直線上を往復する運動のことです。正確には、直線上を往復しているから単振動というわけではないのですが、まずは直線上を往復している運動というイメージを持つと良いでしょう。
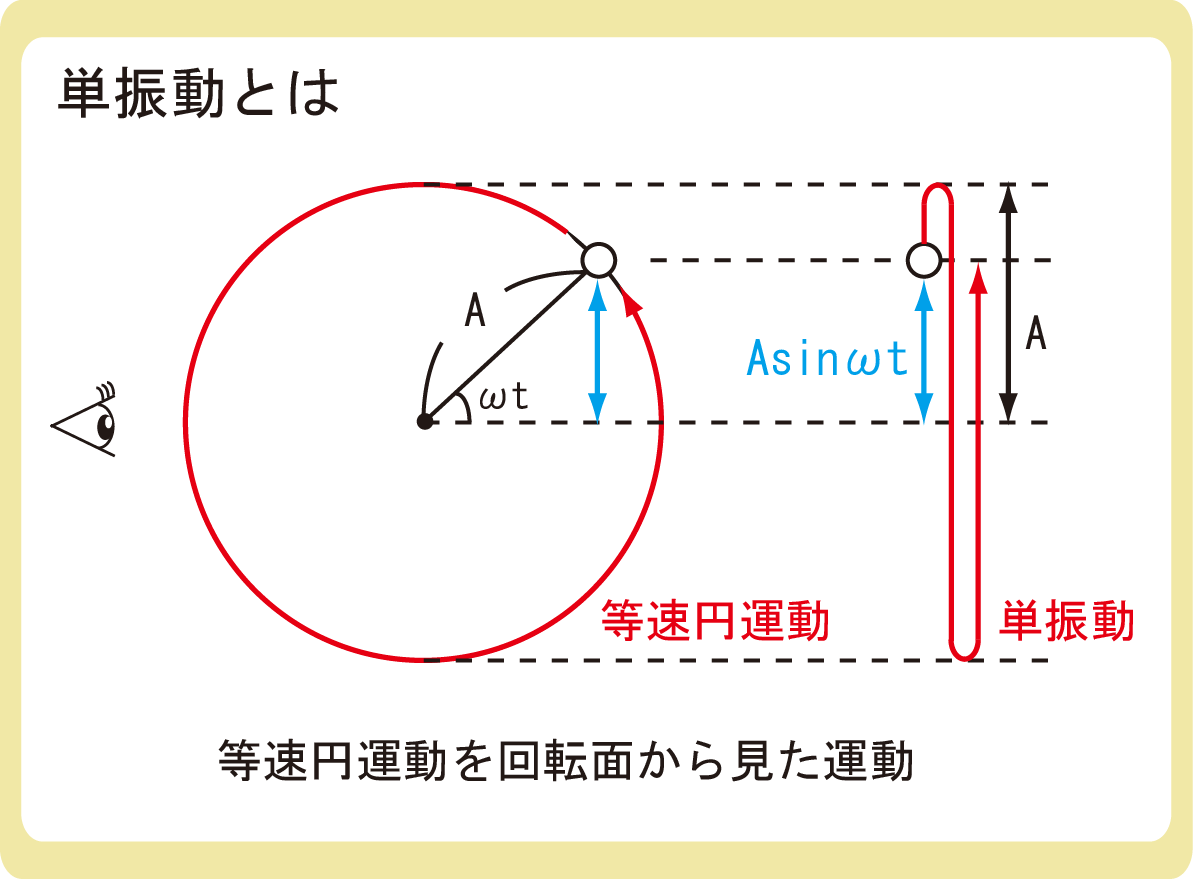
上図のように、等速円運動を回転面の真横から見たときの動きが単振動の動きになると考えることができます。
半径Aの円の円周上を角速度ωで回転している物体の縦の成分のみを考えると単振動になるため、単振動の変位x=Asinωtとなります。なお、ωのことを円運動では角速度と呼びますが、単振動では角振動数と呼びます。単位は[rad/s]で変わりません。
ここで、変位xを時間tで微分すると速度vに、速度vを時間tで微分すると加速度aになることから、
$$x=Asinωt\\
\frac{dx}{dt}=\frac{d(Asinωt)}{dt}\\
v=Aωcosωt$$
$$v=Aωcosωt\\
\frac{dv}{dt}=\frac{d(Aωcosωt)}{dt}\\
a=-Aω^2sinωt$$
と式を導出することができます。
また、
$$\begin{cases} x=Asinωt\\
a=-Aω^2sinωt\end{cases}$$
と連立すると、\(a=-ω^2x\)と表すことができます。
sinとcosの微分は数学3で学ぶ内容なので、もしかしたら知らない人もいるかもしれません。もし微分を習っていない場合は、とりあえず\(a=-ω^2x\)だけ覚えておきましょう。
復元力とは
単振動している物体にはたらく、振動の中心に物体を戻そうとする力
$$F=-Kx$$
(K：定数)
復元力とは、単振動している物体にはたらく、振動の中心に物体を戻そうとする力のことです。
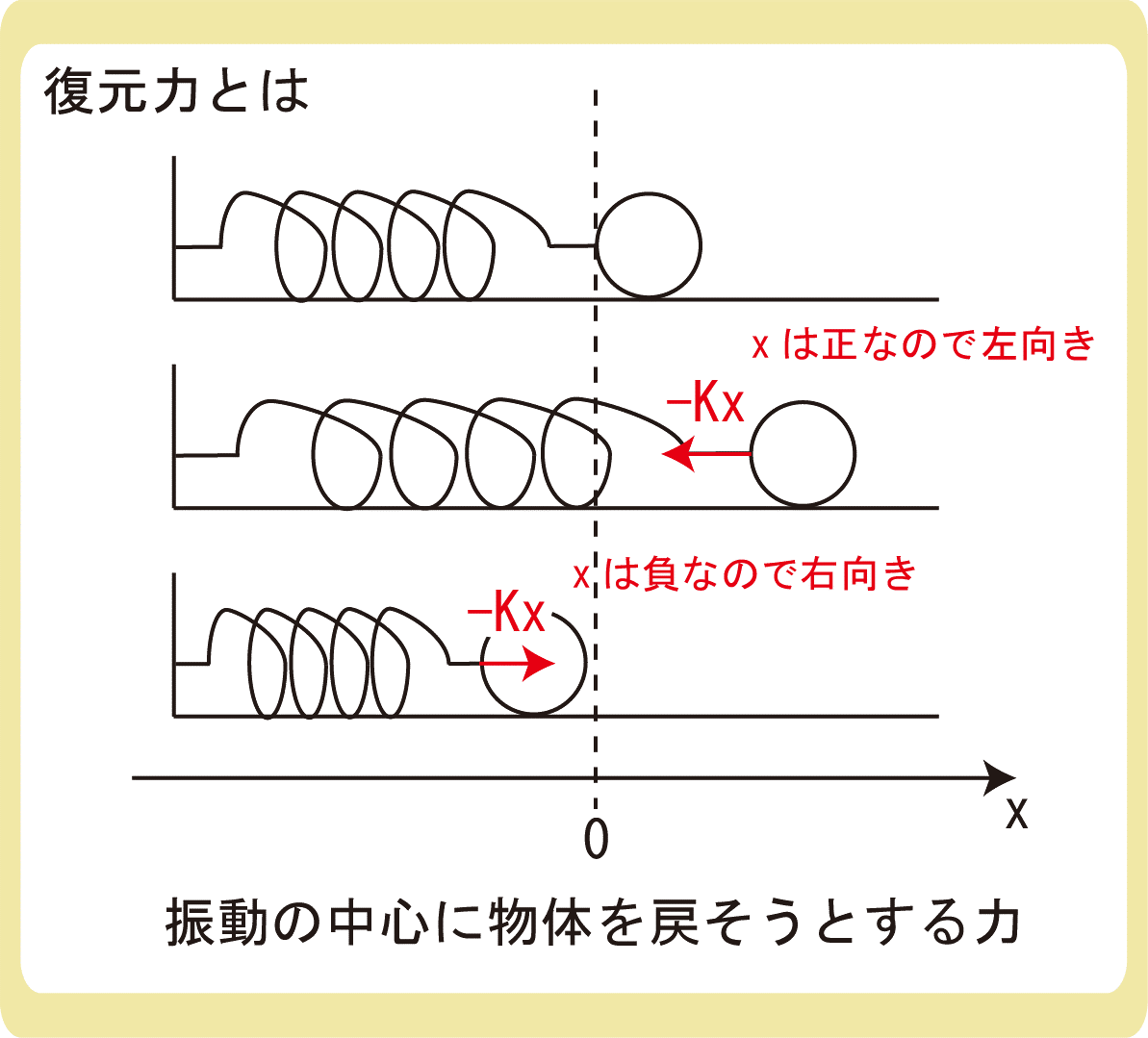
例えば上図のように、水平面上に置いたバネに物体を付け、物体をxだけ伸ばしてから単振動させたとします。
物体には弾性力がはたらくのですが、この弾性力は常に物体の振動の中心を向くため、-Kxと表すことができます。
Kを正の定数であるとすると、上図の真ん中の場合では、xは正なので-Kxの値が負となり力は左向きに、上図の一番下の場合では、xは負なので-Kxの値が正となり力は右向きとなります。
運動方程式を考えると、\(ma=F\)と\(a=-ω^2x\)より、
$$F=ma\\
F=-mω^2x\\
F=-Kx$$
となり、単振動している物体には\(F=-Kx\)という復元力がはたらくと言えます。
逆に言うと、復元力\(F=-Kx\)がはたらく場合、物体は単振動をすると考えます。(大学入試では「復元力がはたらくから単振動と考えることができる」として解く問題をよく見かけます。)
なお、Kは定数であり、様々な数値や物理量が定数となる場合があります。
単振動の周期
$$T=2π\sqrt{\frac{m}{K}}$$
復元力\(F=-Kx\)がはたらいている単振動を考えます。
\(a=-ω^2x\)と\(ma=F\)より、
$$ma=F\\
-mω^2x=-Kx\\
ω=\sqrt{\frac{K}{m}}$$
となります。さらに、円振動にも登場した\(T=\frac{2π}{ω}\)より、
$$T=\frac{2π}{ω}\\
T=2π\sqrt{\frac{m}{K}}$$
となります。
この導出方法は非常に大切です。
これから勉強するバネ振り子と単振り子では、周期Tを覚えておけば問題を解くことは可能ですが、バネ振り子と単振り子以外の単振動のときは、上記のように復元力から角振動数を求め、\(T=\frac{2π}{ω}\)に代入して周期を求める必要があります。
例題
例題1
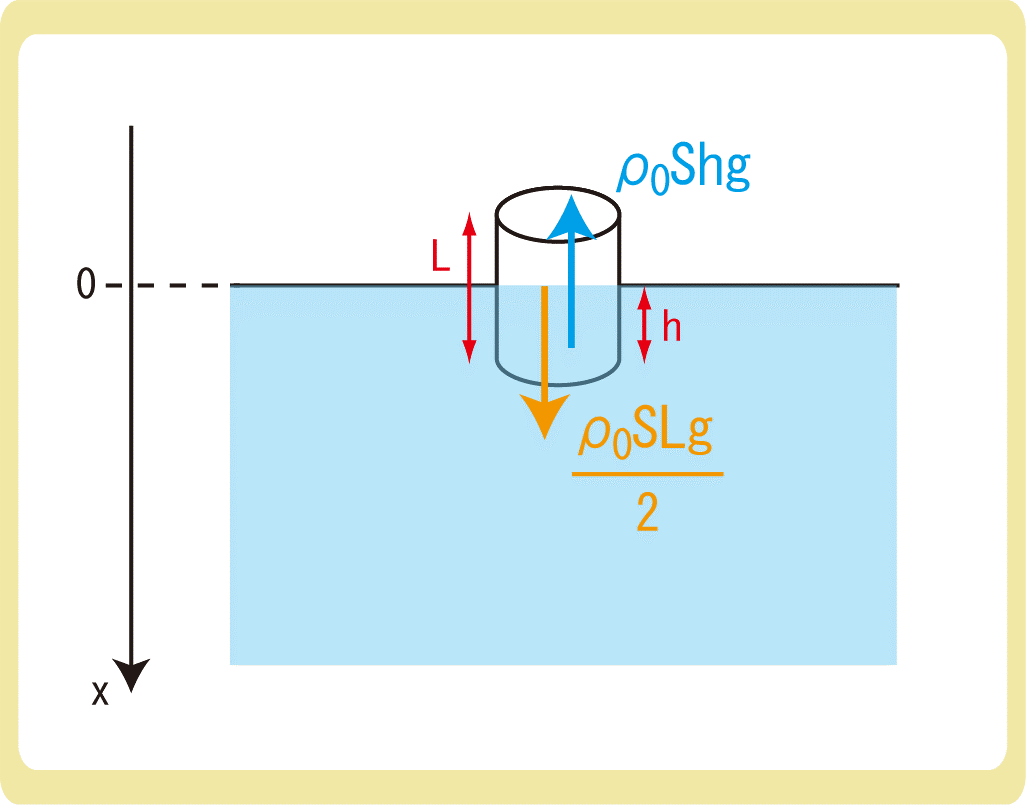
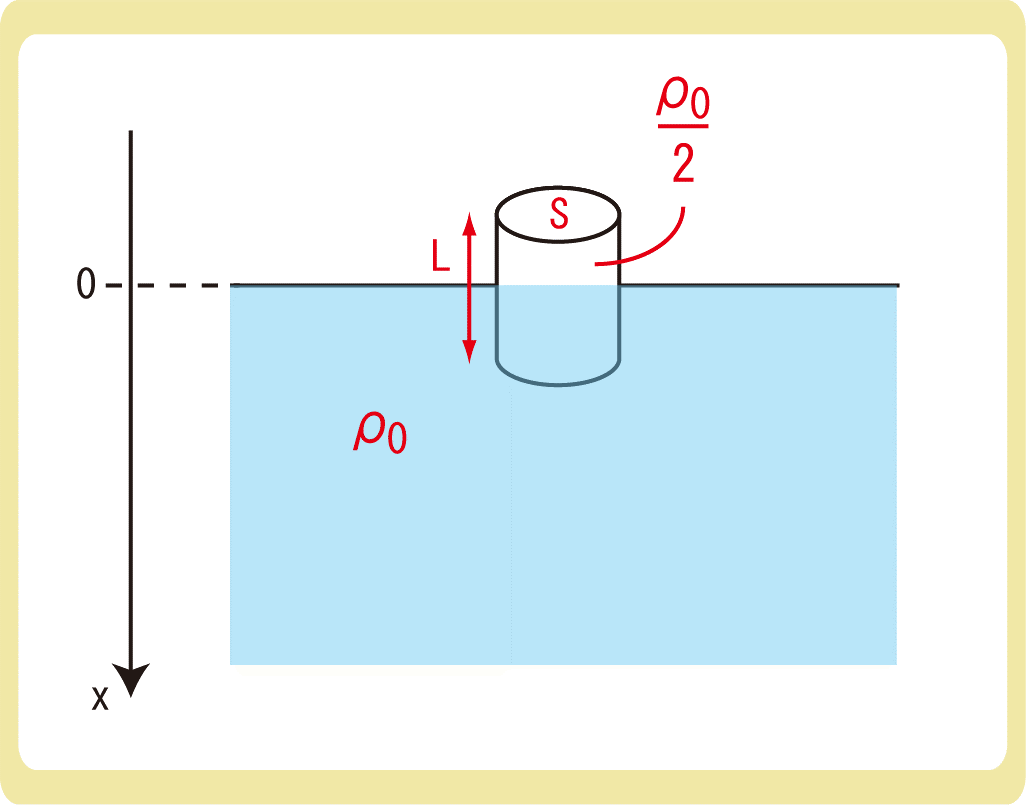
下図のように、密度ρ0の水の中に、長さL、底面積S、密度\(\frac{ρ_0}{2}\)一様な円柱形の物体を沈めた。重力加速度の大きさをgとするとき、以下の各問に答えなさい。なお、空気の抵抗は考えないものとする。
(1)円柱形の物体が静止するように浮かべたとき、水中に沈んでいる円柱の長さはいくらか。
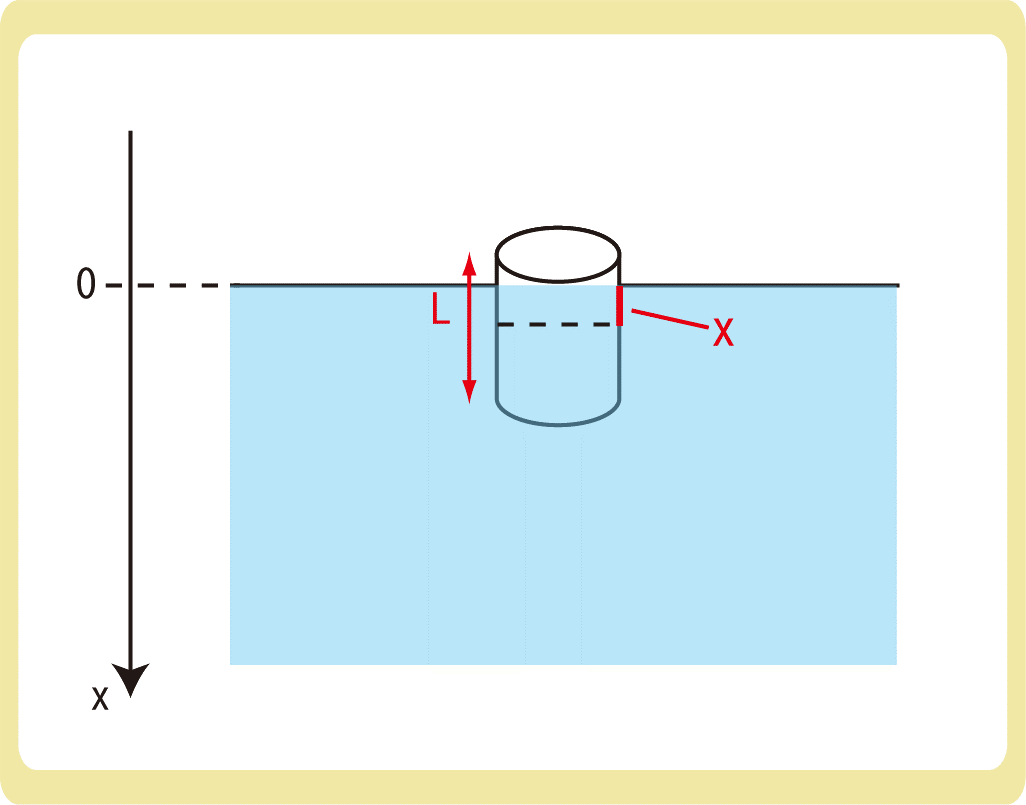
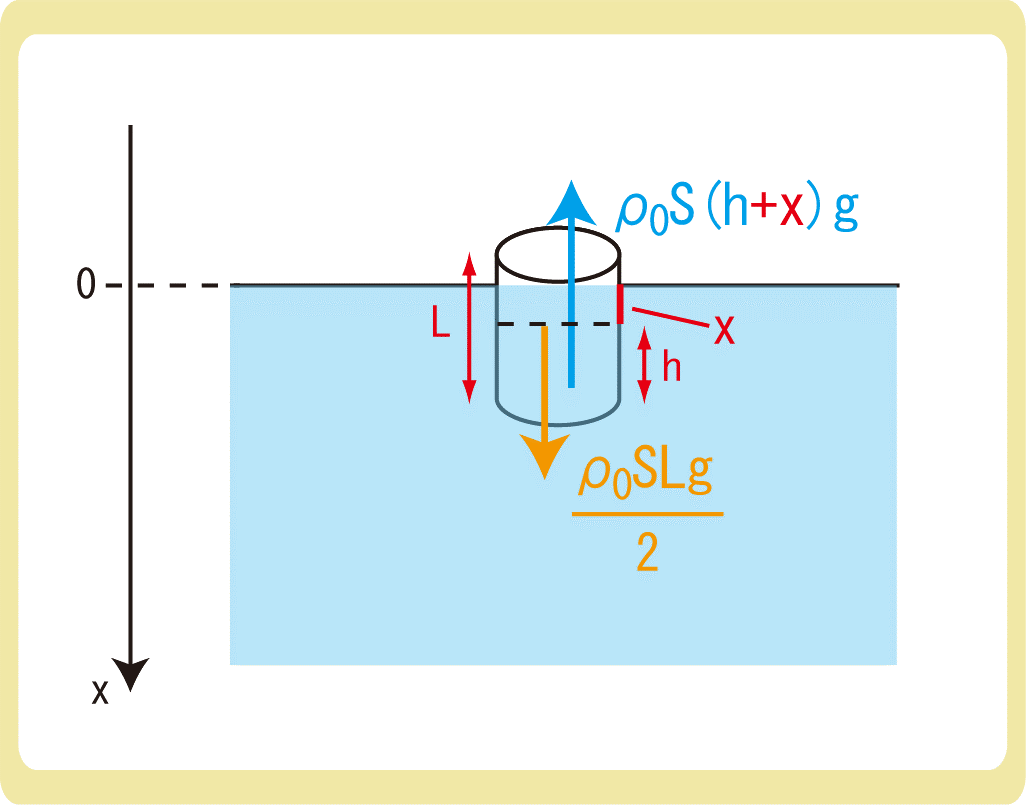
次に、物体を\(\frac{L}{2}+x\)(0<x<\frac{L}{2})だけ沈めてから静かに放したところ、物体は単振動をした。
(2)この単振動の振幅Aを求めなさい。
(3)この単振動の復元力の大きさを求めなさい。
(4)この単振動の周期を求めなさい。
(1)は物理基礎の浮力の問題です。
物体をh(0≦h≦L)だけ沈めたとします。
物体にはたらく重力は普通mgを使うのですが、浮力の問題では質量を与えられることはあまりなく、その代わり密度ρを使うことが非常に多いです。
密度×体積＝質量なので、物体の密度\(\frac{ρ_0}{2}\)×体積\(S×L\)(底面積×高さ)が質量となり、物体にはたらく重力の大きさは
$$\frac{ρ_0SLg}{2}$$
となります。
一方、物体にはたらく浮力の大きさは\(F=ρVg\)(V：沈んでいる体積)で表されるため、\(ρ_0Shg\)となり、物体が静止するためには力がつり合っている必要があるため、
$$\frac{ρ_0SLg}{2}=ρ_0Shg\\
h=\frac{L}{2}$$
∴\(\frac{L}{2}\)
(2)単振動では、力のつりあう位置が振動の中心となるため、(1)より、\(\frac{L}{2}\)沈んだ位置が中心となります。
物体を\(\frac{L}{2}+x\)だけ沈めてから静かに放すということは、振動の中心からxだけ動かしてから放すため、振幅はxとなります。
∴x
(3) (2)のとき、鉛直下向きを正にして、物体にはたらく力を考えてみましょう。
鉛直下向きを正とするとき、物体にはたらく力の合力Fは
$$F=\frac{ρ_0SLg}{2}-ρ_0S(h+x)g$$
となり、\(h=\frac{L}{2}\)を代入すると、
$$F=\frac{ρ_0SLg}{2}-ρ_0S(h+x)g\\
F=\frac{ρ_0SLg}{2}-\frac{ρ_0SLg}{2}-ρ_0Sgx\\
F=-ρ_0Sgx$$
復元力の大きさを求めなさいとのことなので、マイナスを消します。
∴\(ρ_0Sgx \)
(4) (3)より、\(F=-ρ_0Sgx\)となります。
\(ρ_0\)は水の密度なので一定、\(S\)は底面積で一定、\(g\)は重力加速度なので一定、つまり、\(F=-ρ_0Sgx\)は\(F=-Kx\)と表すことができます。(Kは定数、今回は\(K=ρ_0Sg\)。条件によってKの値は変化する。)
単振動では\(F=-mω^2x\)なので(\(a=-ω^2x\), \(ma=F\)を連立している)、
$$F=-mω^2x\\
-Kx=-mω^2x\\
ω=\sqrt{\frac{K}{m}}$$
となり、\(T=\frac{2π}{ω}\)、\(K=ρ_0Sg\)、\(m=\frac{ρ_0SL}{2}\)を使うと、
$$T=2π\sqrt{\frac{m}{K}}\\
T=2π\sqrt{\frac{ρ_0SL}{2ρ_0Sg}}\\
T=2π\sqrt{\frac{L}{2g}}$$
∴\(2π\sqrt{\frac{L}{2g}}\)
まとめ
単振動とは直線上を往復する運動のことなのですが、より正確にいうと、単振動とは復元力\(F=-Kx\)がはたらいているような運動といえます。
単振動では\(a=-ω^2x\)になることから、\(T=2π\sqrt{\frac{m}{K}}\)となります。周期はミカンと覚えておくと楽でしょう。mとKなので、ミカンです。
なお、Kはどのような単振動をするかによって変わる定数です。
これらの式を使って、様々な場合における単振動について学習していきましょう。
