・ばね振り子とは
・鉛直の場合のばね振り子について
単振動では、復元力が\(F=-Kx\)、加速度が\(a=-ω^2x\)、周期は\(T=\frac{2π}{ω}\)であると覚えていますか?
もし分からない場合は、単振動についてもう一度確認しておいた方が良いかもしれませんね。
今回は、単振動の中でもバネが振動している場合についてわかりやすく簡単に解説していきます。
なお、フックの法則\(F=kx\)や、弾性力による位置エネルギー\(U=\frac{1}{2}kx^2\)は物理基礎の内容なので知っている前提で解説をします。
ばね振り子は単振動の中でも最も基本的で頻出の内容なので、しっかり勉強しましょう。
ばね振り子とは
ばねの片方の端を固定し、もう片方の端に物体を付けたもの
$$T=2π\sqrt{\frac{m}{k}}$$
ばね振り子の周期はミカンと覚えると楽。mとkなので、ミカン。
ばね振り子とは、ばねの片方の端を固定し、もう片方の端に物体を付けたもののことです。
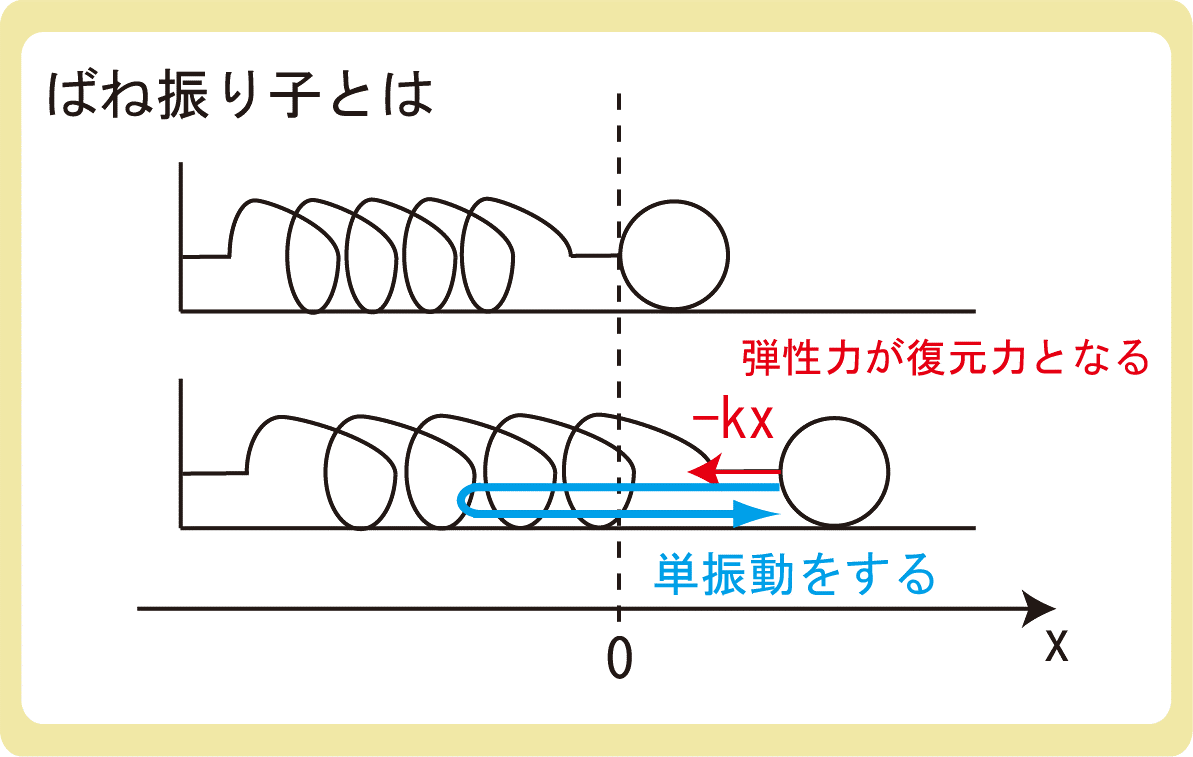
上図のように、ばねを水平に置いたものを水平ばね振り子といいます。
ばねについた物体を引っ張り(押し込み)静かに手放すと、ばねについた物体が単振動をします。
このとき、ばねの弾性力が復元力となるため、\(F=-kx\)と\(a=-ω^2x\)、\(T=\frac{2π}{ω}\)より、
$$F=-kx\\
ma=-kx\\
-mrω^2=-kx\\
ω=\sqrt{\frac{k}{m}}$$
$$T=\frac{2π}{ω}\\
T=2π\sqrt{\frac{m}{k}}$$
となります。ばね振り子の周期はミカンと覚えると楽です。mとkなので、上から読むとミカンです。
ばね振り子の周期が\(T=2π\sqrt{\frac{m}{k}}\)となることを覚えておくと、色々な問題を簡単に解くことができます。
可能であれば、ばね振り子の周期の導出を覚えておきたいところですが、とりあえずミカンと覚えておくと楽です。
例題
例題1
下図のように、ばね定数kのバネの片方の端を固定し、もう一端に質量mの物体を付け、水平に置いた。物体をバネの自然の長さからAだけ伸ばし、静かに手放したところ、物体は単振動をした。以下の各問に答えなさい。
(1)この物体の最大の速さはいくらか。
(2)この単振動の周期を求めよ。
(3)はじめに物体を2Aだけ伸ばしてから静かに手放した場合、単振動の周期は(2)の何倍になるか。
(4)物体の質量を2mにした場合、単振動の周期は(2)の何倍になるか。
鉛直の場合のばね振り子について
振動の中心は、自然の長さではなく、力のつり合う位置となる
ばね振り子を鉛直にした場合、振動の中心は自然の長さではなく力のつり合う位置となります。
簡単に言うと、鉛直ばね振り子では、ばねが自然の長さからどれくらい伸び縮みしているのかではなく、ばねが力のつり合いの位置からどれくらい離れているかのみを考えます。
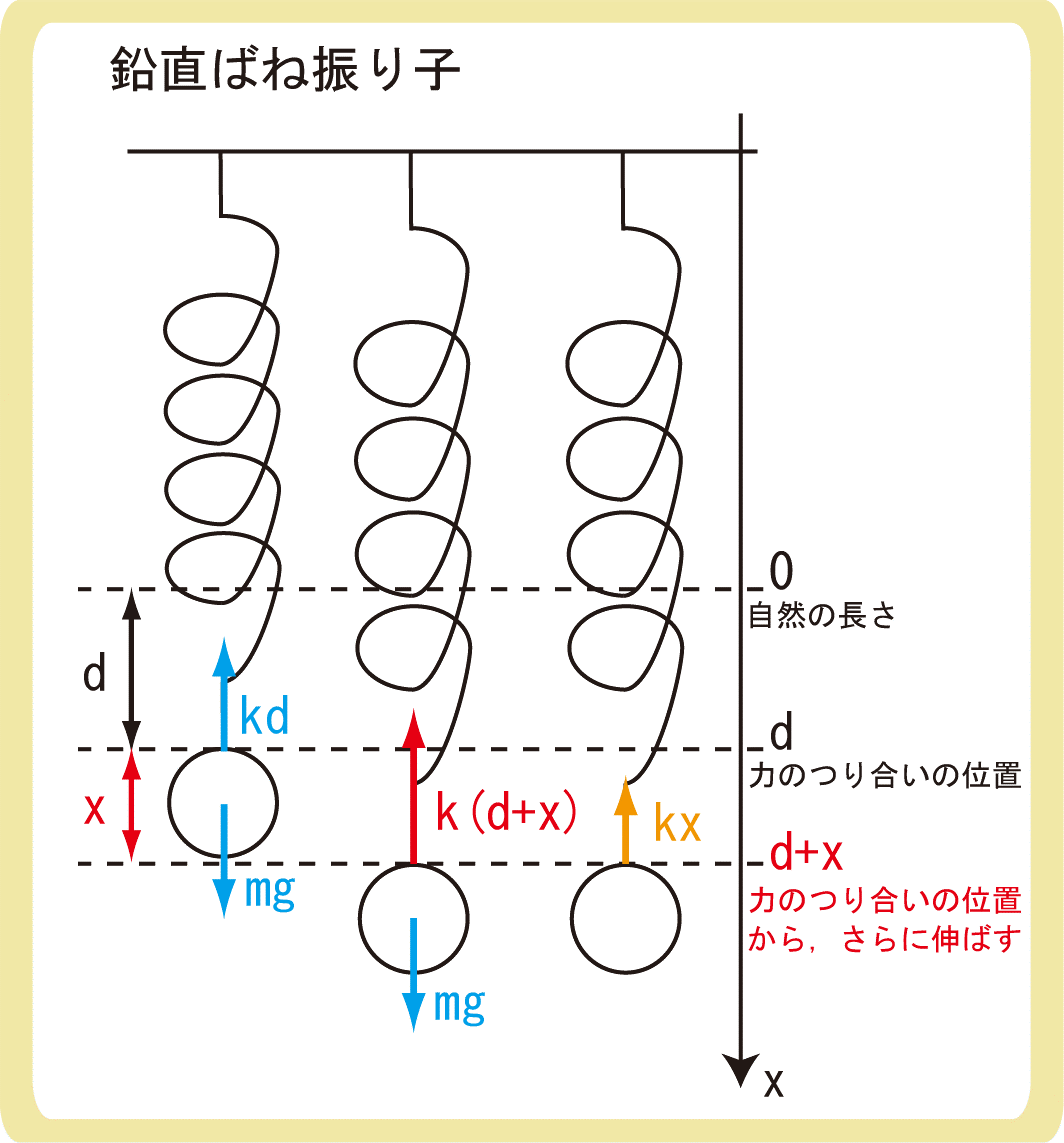
上図のような場合を考えます。
一番左のように、物体にはたらく力がつり合っているとき、
$$mg=kd$$
と表すことができこの合力ます。
次に、真ん中のように、バネをつり合いの位置からさらにxだけ伸ばしたときを考えます。
このとき、物体にはたらく力は、下向きの重力mgと上向きの弾性力k(d+x)なので、合力は
$$F=mg-k(d+x)$$
になります。ここで、\(mg=kd\)であることを利用すると、
$$F=mg-kd-kx\\
F=-kx$$
となり、これが復元力となります。
よく見ると、復元力のxは自然の長さからの変位d+xではなく、力のつり合いからの変位xとなっていることが分かります。
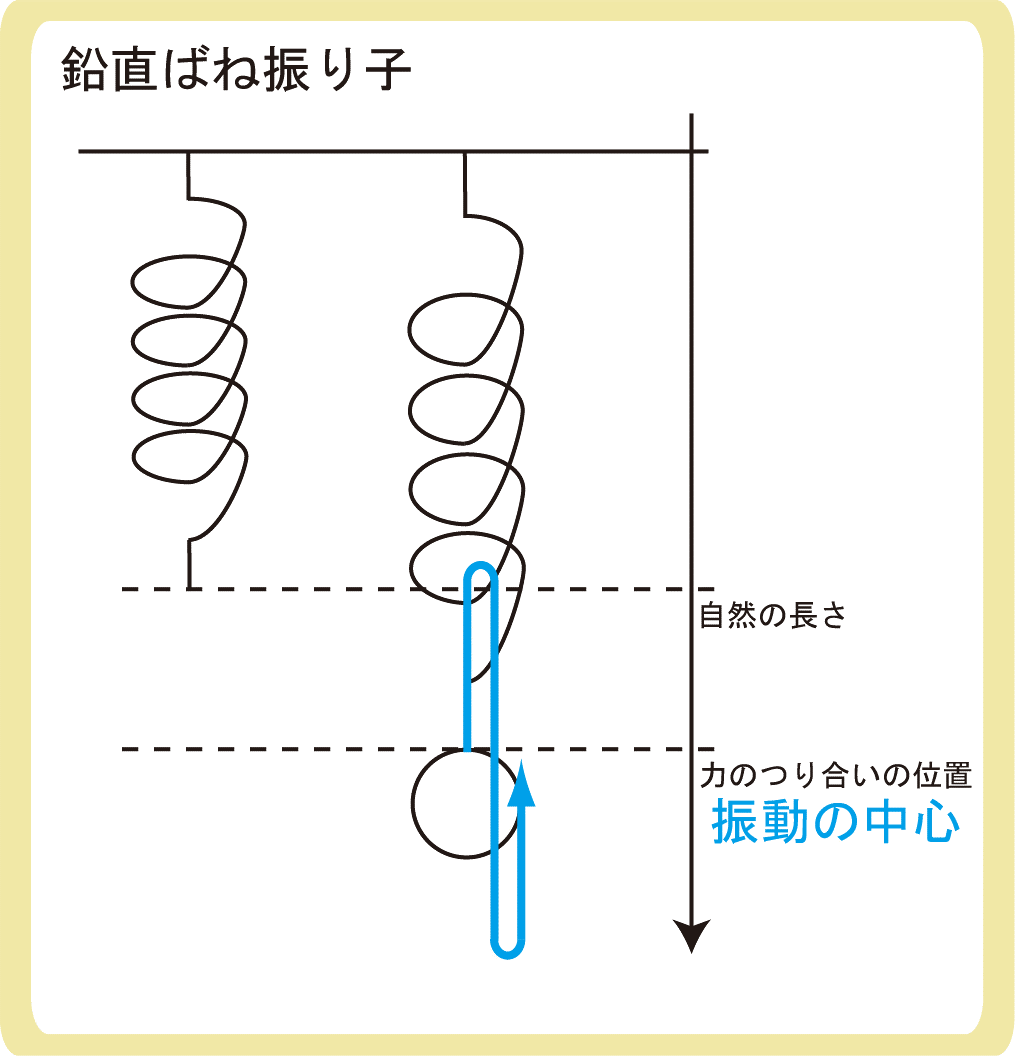
つまり、鉛直ばね振り子の振動の中心は、自然の長さではなく力のつり合いの位置であると考えます。
もちろん、振幅の大きさは、力のつり合いの位置からどれくらい離れているかになるのです。
また、鉛直ばね振り子でも復元力は\(F=-kx\)となるため、周期Tは\(T=2π\sqrt{\frac{m}{k}}\)となります。mとkなのでミカンと覚えておくと楽でしょう。詳しい式の導出は前回の内容を確認してください。
例題
例題2
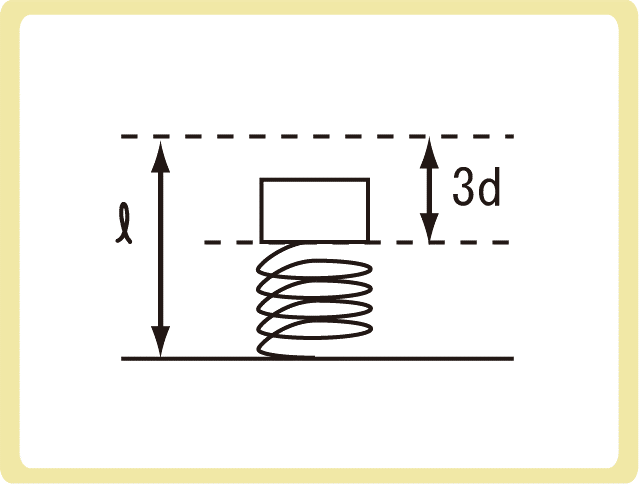
下図のように、自然の長さ\(l\)のばねの片方の端を固定し、もう片方の端に質量mの物体を付けたところ、ばねの長さがdだけ縮み静止した。このバネを3dだけ縮めてから静かに手放すと、物体は単振動をした。以下の各問に答えなさい。ただし、重力加速度の大きさをgとする。
(1)このばねのばね定数を求めなさい。
(2)この単振動の周期を求めなさい。
(3)この物体の最大の速さを求めなさい。
まとめ
ばねを単振動させるとき、弾性力が復元力となります。
復元力から周期を求めると、\(T=2π\sqrt{\frac{m}{k}}\)となり、ミカンと覚えると楽です。
ばねに繋がられた物体を鉛直に単振動させるとき、振動の中心は力のつり合う位置となります。
従って、バネの長さを考えるときも、自然の長さではなく、力のつり合う位置からの長さを考えることで問題を解きましょう。












