・第一宇宙速度とは
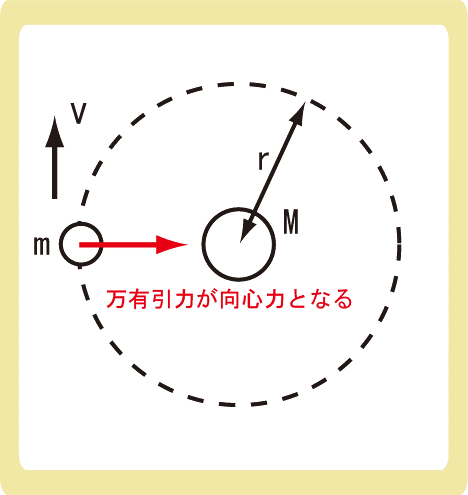
・万有引力と円運動について
「リンゴは落ちるのになぜ月は落ちないのか」の答えは「月は落ち続けているが、月が落ちる頃には地面も曲がり地面が下がるため、月と地面の距離が変わらないから」です。
万有引力と円運動を組み合わせたとき、月が落ちない理由を理解することができます。
今回は、万有引力と円運動を使い、第一宇宙速度とは何かについてわかりやすく簡単に解説していきます。
第一宇宙速度とは
人工衛星が地表すれすれを円運動するために必要な速度のこと
$$v=\sqrt{gR}$$
第一宇宙速度とは、人工衛星が地表すれすれを円運動するために必要な速度のことです。
水平投射を思い浮かべて下さい。ボールを水平に投げると真っ直ぐ飛んで落ちますね。もっと勢いよく投げるとボールはより遠くに落ちます。
もっともっともっと速くボールを投げるとどうなるでしょうか。
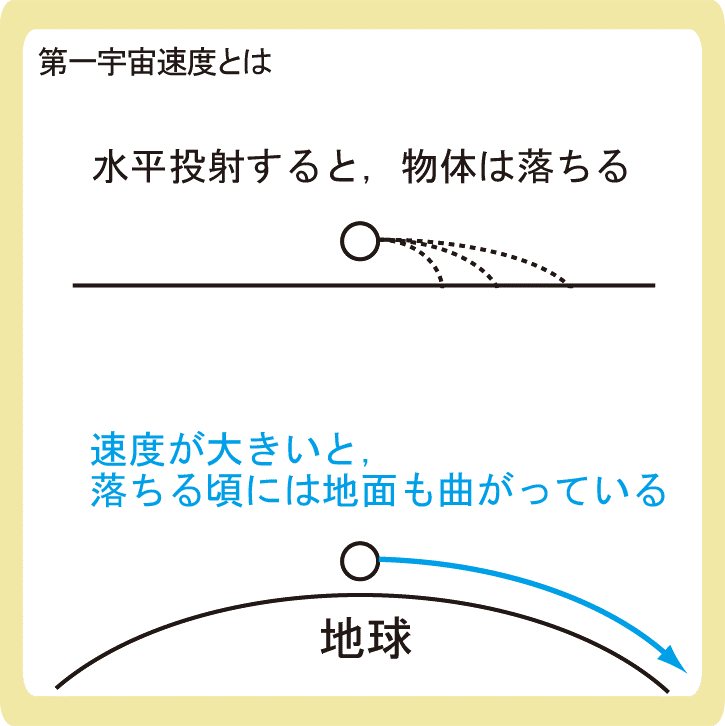
ある速度を超えると、ボールが少し落ちてもその分地面も低くなるので永遠に落ちないという現象が起きます。
上図のように、地表すれすれで水平投射をしたとき物体が落ちなくなるような速度のことを第一宇宙速度といいます。
このとき、物体は地球の周りを円運動していると考えられるため、地球の周りを周っている人工衛星についての例題を解いて、万有引力と円運動について考えてみましょう。
例題1
質量mの人工衛星が質量M、半径Rの地球の中心からrの距離で等速円運動をしている。このときの人工衛星の速さを求めよ。ただし、重力加速度の大きさをgとする。
第一宇宙速度の式の導出
第一宇宙速度は、地表すれすれを円運動するために必要な速度のことです。
上の例題1では、地球からrはなれた場合を考えました。
r=Rのとき、地球すれすれを円運動している人工衛星といえるため、
上の例題1の解答を用いると
$$v=\sqrt{\frac{gR^2}{r}}\\
v=\sqrt{\frac{gR^2}{R}}\\
v=\sqrt{gR}$$
となり、これが第一宇宙速度の式となります。
まとめ
第一宇宙速度とは、地表すれすれを円運動するために必要な速度のことです。
万有引力が向心力となることから導出すると、\(v=\sqrt{gR}\)となります。