万有引力による位置エネルギーと第二宇宙速度

2024 1/31

2024-01-31

URLをコピーしました！

この記事で学べる内容

・万有引力による位置エネルギーとは

・無限遠とは

・第二宇宙速度とは

物理基礎で位置エネルギーを勉強したことを覚えていますか。

重力による位置エネルギーはmgh、弾性力による位置エネルギーは$\frac{1}{2}kx^2$です。この2つの式の導出と同様に、万有引力による位置エネルギーを考えてみましょう。

今回は、万有引力による位置エネルギーとは、第二宇宙速度とはについて、わかりやすく簡単に解説していきます。

万有引力による位置エネルギーの公式
第二宇宙速度とは
例題
- 例題1 第二宇宙速度の求め方
- 例題2
まとめ

万有引力による位置エネルギーの公式

万有引力による位置エネルギー

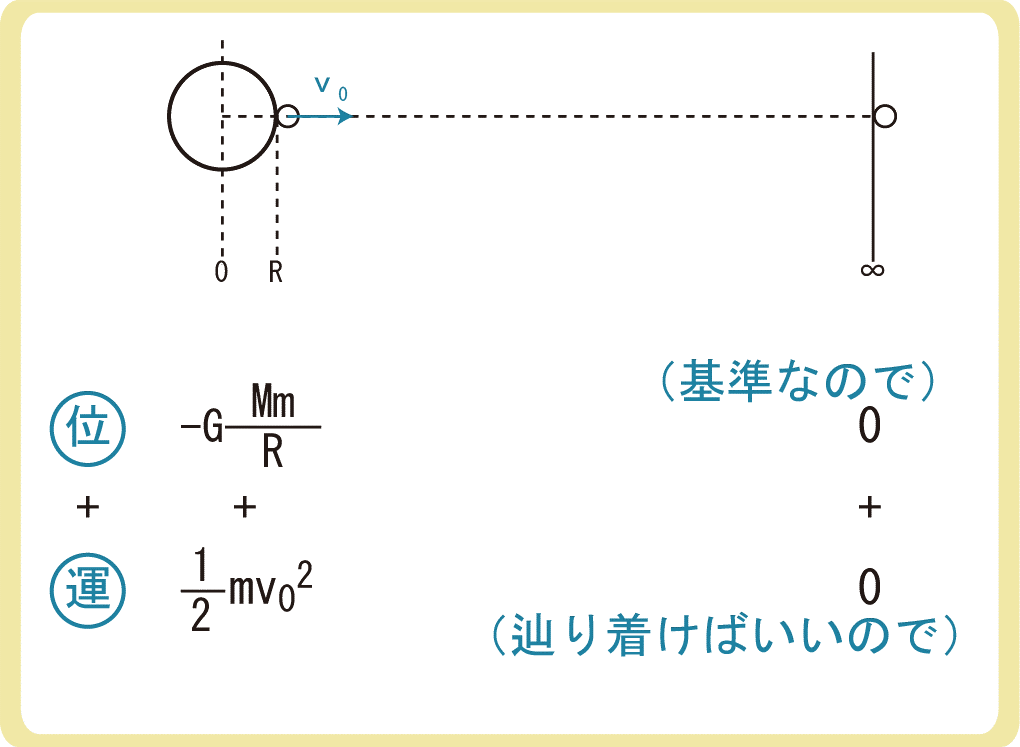
無限遠を基準とすると

$$U=-G\frac{Mm}{r}$$

万有引力による位置エネルギーの公式は、無限遠を基準とすると$U=-G\frac{Mm2}{r}$という式になります。

そもそも、位置エネルギーとは仕事をするポテンシャルのこと、つまり、どれくらい仕事ができるのかを表します。

仕事とは力・距離（力と平行な成分）で表される量であり、W=FxやW=Fs等と紹介されることが多いです。

万有引力による位置エネルギーも、重力による位置エネルギーや弾性力による位置エネルギーと同様に、力Fと距離rのグラフを描くことで求めることができます。

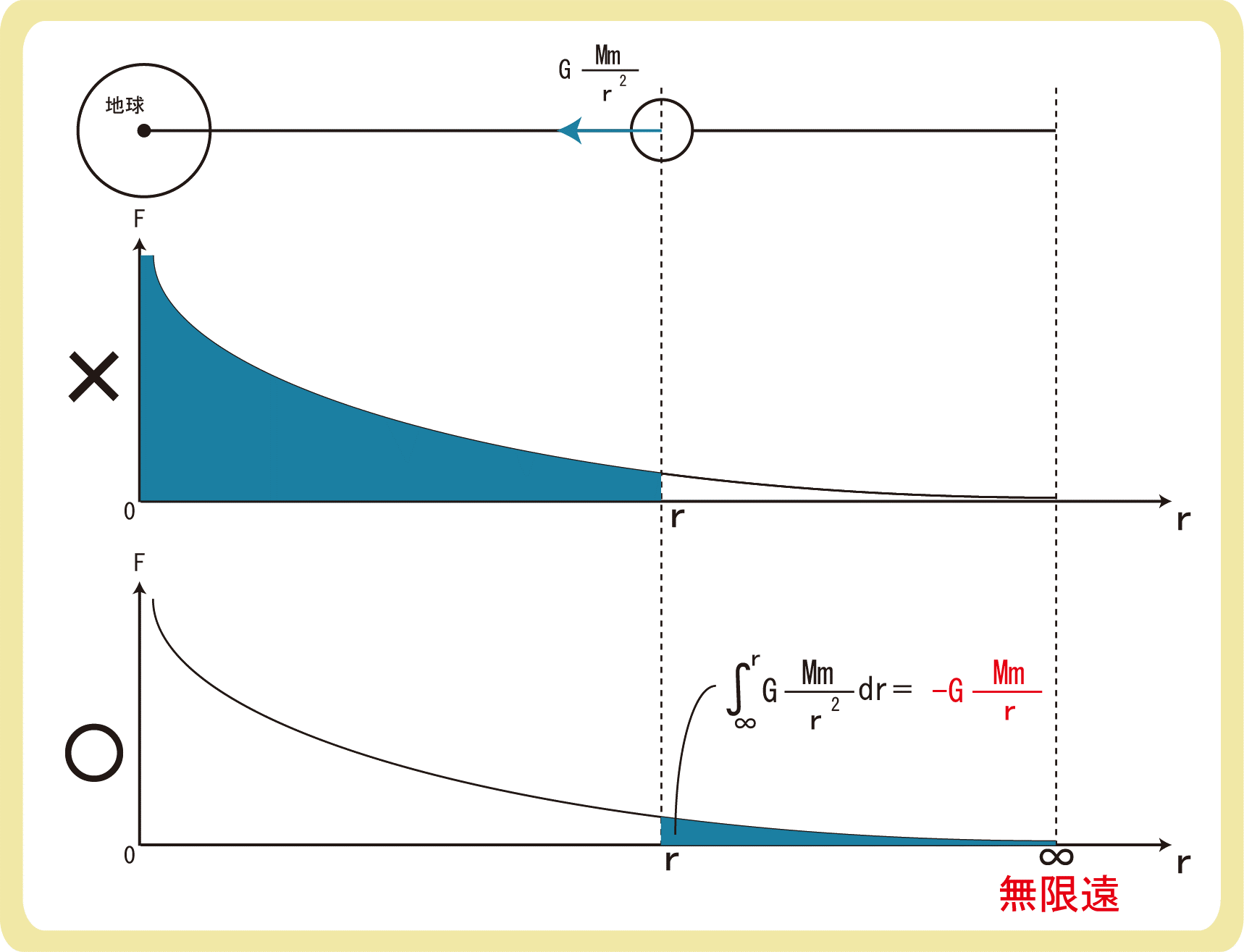
上図の一番上のように、地球の中心からr離れた物体が持つ位置エネルギーを考えます。

重力による位置エネルギーや弾性力による位置エネルギーのように、グラフの面積を求めることで位置エネルギーを求めることができるのですが、四角形でも三角形でもないので、簡単に求めることができません。

上図のようなグラフと軸に囲まれた面積を求めるためには、数Ⅲで勉強する積分を使います。
※数3の積分を勉強していない人は、公式が$U=-G\frac{Mm}{r}$であることを覚えるしかないでしょう。

しかし、地球の中心を基準として積分の計算をすると

$$\begin{eqnarray}U&=&\int_{0}^{r} (G\frac{Mm}{r^2})dr\\
&=&\left[\frac{GMm}{-r}\right]_0^r\end{eqnarray}$$

となり、分母に0を代入できないため計算ができなくなってしまいます。

そこで、地球ではなく無限遠という限りなく遠い点を基準として考えると、

$$\begin{eqnarray}U&=&\int_{∞}^{r}(G\frac{Mm}{r^2})dr\\
&=&\left[-\frac{GMm}{r}\right]_∞^r\\
&=&-\frac{GMm}{r}-(-\frac{GMm}{∞})\\
&=&-\frac{GMm}{r}+0\\
&=&-\frac{GMm}{r}\end{eqnarray}$$

のように、積分区間が∞～rとなるため計算することができます。

従って、無限遠を基準としたときの万有引力による位置エネルギーは$U=-G\frac{Mm}{r}$となります。

第二宇宙速度とは

第二宇宙速度

物体が地球まで戻ってこなくなるような速度のこと

$$v=\sqrt{2gR}$$

第二宇宙速度とは、物体を投げたとき、物体が地球まで戻ってこなくなるような速度のことです。

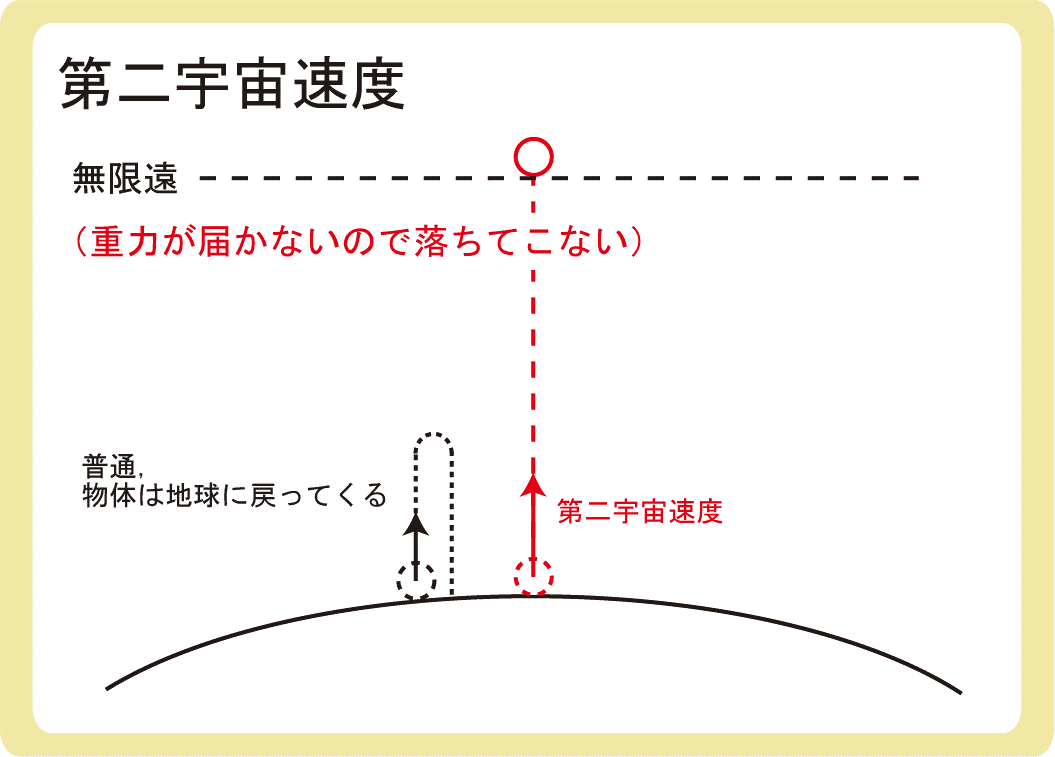
物体を鉛直上向きに投げるとき、普通は重力によって物体が地球に戻ってきますが、投げ上げたときの速さがある大きさを超えると、物体が重力の届かない無限遠まで到達するため地球に戻ってこなくなってしまいます。

このような、物体を投げたとき(投げ上げでなくても良い)、ギリギリ無限遠に到達し地球に戻ってこなくなるような速度のことを第二宇宙速度といいます。

第二宇宙速度を求めるため、以下の例題を解いてみましょう。

例題

例題1 第二宇宙速度の求め方

地上から打ち上げられた物体が地表に戻らないような速度(第二宇宙速度)を求めなさい。ただし、地球の半径をR、重力加速度の大きさをgとする。

解答

第二宇宙速度を求めるためには、エネルギー保存の法則を使います。
万有引力による位置エネルギーの公式$U=-G\frac{Mm}{r}$を覚えておきましょう。

物体の質量をm、地球の質量をM、万有引力定数をGとし、物体の初速度をv₀とします。
このとき、無限遠を基準とすると、地球上での万有引力による位置エネルギーは$U=-G\frac{Mm}{R}$になります。(位置がRなので、分母がrではなくRになっている)
また、地球上での運動エネルギーは初速度がv₀なので$\frac{1}{2}mv_0^2$です。

一方、物体が無限遠に達したとき、この物体がもつ万有引力による位置エネルギーは0となります。無限遠が基準なので位置エネルギーは0です。
また、物体が無限遠に達したとき、運動エネルギーが0以上であれば、地球に戻らず進み続けると考えることができます。物体が無限遠に達したときの運動エネルギーが0のときが、ギリギリ物体が地球に戻らなくなるときといえますね。

エネルギー保存の法則より

$$\frac{1}{2}mv_0^2+(-G\frac{Mm}{R})=0+0$$

となるので、この式を計算すると

$$v_0=\sqrt{\frac{2GM}{R}}$$

と求めることができます。あとは、$gR^2=GM$を使うことで、

$$v_0=\sqrt{\frac{2GM}{R}}\\
v_0=\sqrt{\frac{2gR^2}{R}}\\
v_0=\sqrt{2gR}$$

となります。

∴$\sqrt{2gR}$

これが、第二宇宙速度の求め方です。

例題2

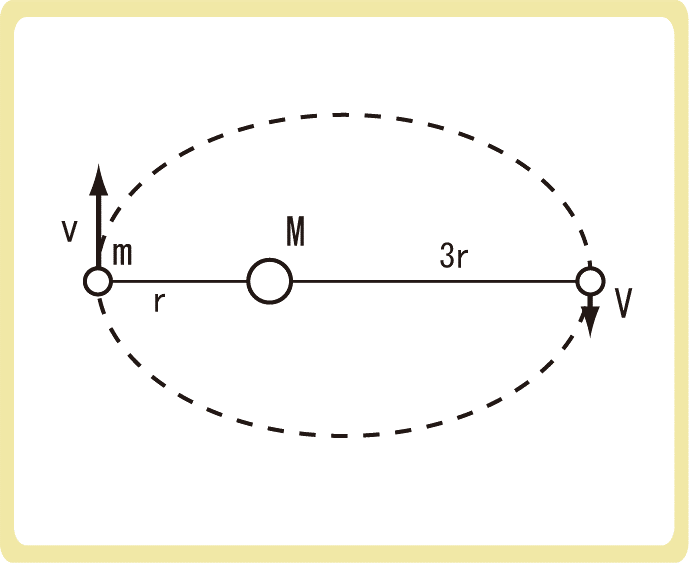
下図のように、質量Mのとある恒星を1つの焦点として、質量mの惑星が楕円軌道上を運動している。恒星と惑星の近日点の距離をr、遠日点の距離を3rとし、万有引力定数をGとするとき、近日点の速さ$v$と、遠日点の速さ$V$をそれぞれ求めなさい。

解答

どの問題でも同じですが、$v$と$V$、求める量が2つあるときは、2つ以上の式を立てます。
ケプラーの第2法則(面積速度一定の法則)と、エネルギー保存の法則の2つの式を使って問題を解いていきましょう。

ケプラーの第2法則(面積速度一定の法則)より

$$\frac{1}{2}×r×v=\frac{1}{2}×3r×V・・・①$$

無限遠を基準とするとき、エネルギー保存の法測より、

$$\frac{1}{2}mv^2-G\frac{Mm}{r}=\frac{1}{2}mV^2-G\frac{Mm}{3r}・・・②$$

この2つの式を計算することで、答えを求めることができます。

①より、

$$V=\frac{v}{3}・・・③$$

これを②に代入すると、

$$\frac{1}{2}mv^2-G\frac{Mm}{r}=\frac{1}{18}mv^2-G\frac{Mm}{3r}\\
\frac{1}{2}mv^2-\frac{1}{18}mv^2=-G\frac{Mm}{3r}+G\frac{Mm}{r}\\
\frac{8}{18}mv^2= G\frac{2Mm}{3r}\\
v^2=\frac{3M}{2r}\\
v=\sqrt{\frac{3M}{2r}}$$

これを③に代入し、

$$V=\frac{1}{3}×\sqrt{\frac{3M}{2r}}\\
V=\sqrt{\frac{M}{6r}}$$

∴$v=\sqrt{\frac{3M}{2r}}$、$V=\sqrt{\frac{M}{6r}}$