ハイゼンベルクの不確定性原理を知っていますか?
不確定性原理は物理や化学で登場する内容ですが、科学という垣根を越えて全世代的に有名となっている原理であるため、一度は耳にしたことがあるのではないでしょうか。
今回は、物理教師である私が、ハイゼンベルクの不確定性原理について分かりやすく簡単に説明していこうと思います。
ハイゼンベルクの不確定性原理とは何か
ハイゼンベルクの不確定性原理とは
ハイゼンベルクの不確定性原理とは、ある物理量Aと、ある物理量Bを同時に正確に計測することができないという原理です。
主に、素粒子の「位置」と「運動量」を同時に正確に計測できないという意味で使われているのを多く見かけます。
運動量とは質量×速度のことですが、単純に「速さ」というイメージを持ってもらっても大丈夫です。本当は運動量という言葉を使いたいのですが、分かりやすさ重視で速さという言葉を使います。
電子の「位置」を正確に測ろうとすると「速さ」が正確に測れなくなり、「速さ」を正確に測ろうとすると「位置」が正確に測れなくなる
というイメージ
日常生活において、「位置」と「速さ」を同時に知ることは容易です。
今目の前にあるスマホ(もしくはPC)の位置は分かりますし、きっと速さは0でしょう。
しかし、ハイゼンベルクの不確定性原理によると、電子などの素粒子では、「位置」と「速さ(運動量)」を同時に正確に測ることができないのです。
ポイントは”測定可能かどうか”
ハイゼンベルクの不確定性原理を理解する上で大切な点は”測定可能かどうか”という点です。
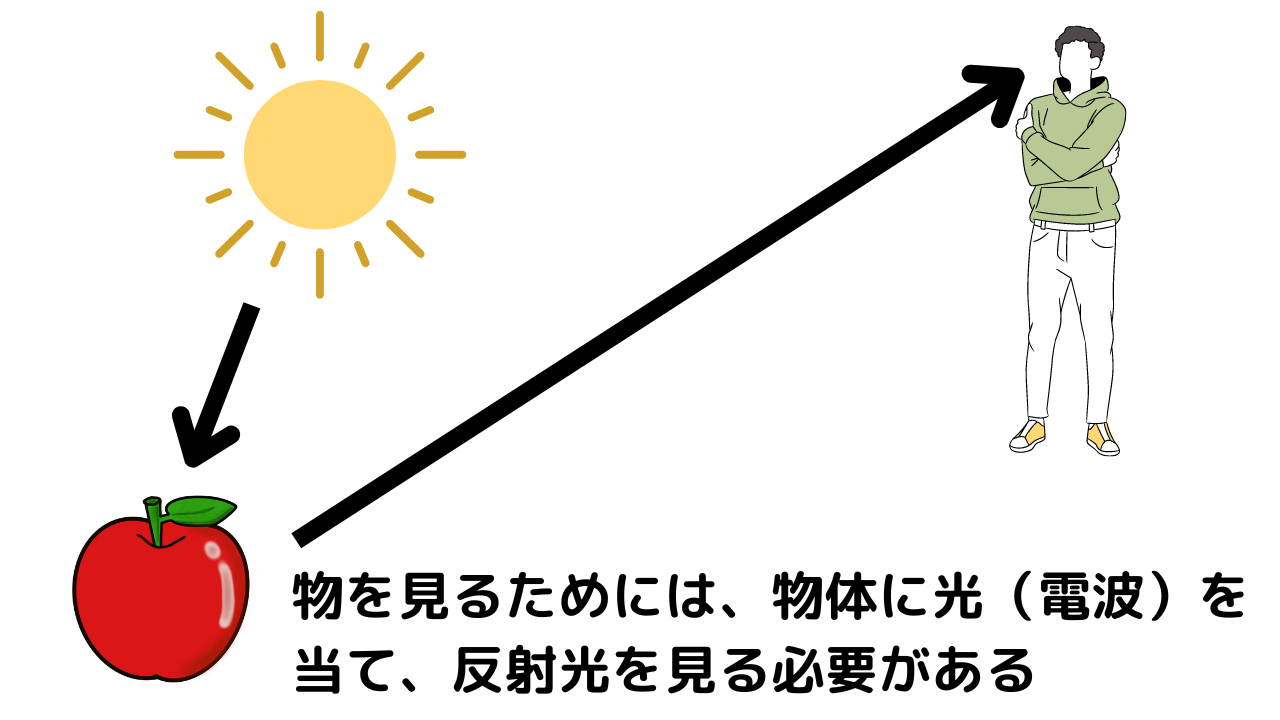
そもそも物体の位置は、物体に電波を当て、物体に衝突した電波を観測することで知ることができます。
人間の場合、物体に光を当て、反射光を見ることで物体の位置が分かりますよね。
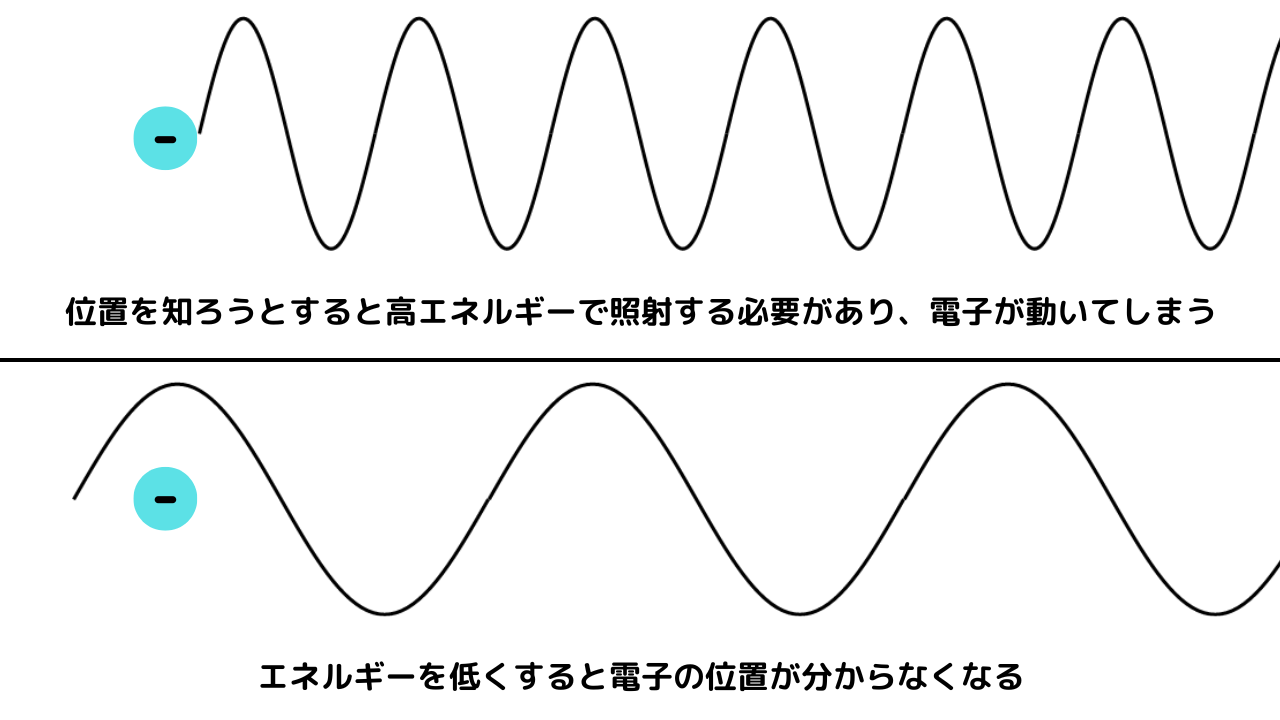
電子の位置を知るためにガンマ線を照射すると想定した場合、電子の位置を知るために波長を短く(エネルギーを大きく)すると、ガンマ線に当たった電子が動いてしまうため、電子の位置は分かっても速さは分かりません。
波長を長く(エネルギーを小さく)した場合、エネルギーが小さくなれば電子は動きにくくなりますが、波長が長くなってしまうため電子をすり抜ける可能性が高くなり、位置が分かりにくくなってしまいます。
位置と運動量の不確定性を、ハイゼンベルクは以下のような式として出しています。
$$ε_xη_p≧\frac{h}{4π}$$
\(ε_x\):位置の誤差、\(η_p\):運動量の擾乱、\(h\):プランク定数
位置の誤差を0に近づければ近づけるほど、運動量の擾乱(運動量が乱される量)が大きくなっていく、逆もまた然り。
これが、ハイゼンベルクの不確定性原理の考え方です。
ケナードの不等式
$$δ_xδ_p≧\frac{h}{4π}$$
\(δ_x\):位置の標準偏差、\(δ_p\):運動量の標準偏差
ハイゼンベルクの不確定性原理と混同してしまうものとして、ケナードの不等式というものがあります。
ハイゼンベルクの不確定性原理では位置の誤差と運動量の擾乱の積でしたが、ケナードの不等式は位置と運動量、それぞれの標準偏差の積となっています。
簡単に言うと、粒子をどんなに正確な測定をしたとしても必ず測定結果にばらつきが現れ、そのゆらぎの積は\(\frac{h}{4π}\)以下にならないという意味となっています。
全く同じ状況で何度正確に測定したとしても、そもそも粒子の位置や運動量の値がランダムで変化することがゆらぎであり、測定誤差とは異なります。
ハイゼンベルクの不確定性原理は測定の不確定性を表していますが、ケナードの不等式は粒子そのものの不確定性を表している点で違います。
ハイゼンベルクの不確定性原理は、原理という名前の通り、他の法則から導き出されたものではありませんが、ケナードの不等式は量子力学から導き出された式なので原理ではありません。
一般的には、不確定性原理というとハイゼンベルクの方として使うことが多いですが、物理学者の間ではケナードの不等式の方をよく使うので、そういう意味でも混同してしまうみたいです。
不確定性原理は結局何が言いたいのか
元々、量子力学が登場する前(ニュートン力学=古典力学 のみの時代で)は、大雑把に言うと、物体の位置や速度が分かれば物体がこれからどうなるか必ず分かるということが信じられていました。
物を落とせば何秒後に地面に着くか分かりますし、大砲を放てばどこに落ちるかも計算で出せました。
しかし、ミクロの世界になると、そもそも粒子の位置と速度を同時に正確に知ることができないため、粒子がどのように動くのか・どこにいるのかを確率でしか求めることができません。
つまり、未来は確定しておらず、確率によって変化していることが量子力学で判明したのです。
簡単に言うと、一年後の天気は今の時点で確定しておらず、どうなるのか確率でしか分からないのです。
この辺の詳細は、決定論と非決定論として別の機会に話したいと思います。
まとめ
ハイゼンベルクの不確定性原理は、「位置」と「運動量(イメージのような速さ)」を同時に正確に知ることができないという原理です。
本当は「位置」と「運動量」以外にも組み合わせがあるのですが、「位置」と「運動量」が最もよく例として挙げられています。
ハイゼンベルクの「不確定性」は測定誤差と擾乱(運動量の乱された量)によるものですが、似たようなものとして、量子そのものの「不確定性」について言及したケナードの不等式があります。
この2つは教科書レベルでも混同しているものもあるくらい、非常にややこしいです。
物理学者以外の人が使う不確定性原理は、”「位置」と「運動量」を同時に正確に知ることができない原理”だと理解しておけば大丈夫です。












