「確率は収束する」を勘違いしてる人が多すぎる 日常生活で確率は収束しないし試行回数も足りていない

「確率は収束する」

間違いなく確率は収束します。

しかし、「確率は収束する」を勘違いして理解している人があまりにも多いです。

一体なぜ勘違いしてしまう人が多いのでしょうか。

今回は、「確率は収束する」の意味と典型例な誤用について解説していきます。

「確率は収束する」誤用の典型例

例1

例2

例3

誤用の原因その①「代数の法則」を中途半端に知っている

「確率は収束する」を誤用する原因は2つの勘違いから来ています。

1つ目の原因は、代数の法則をなんとなーく知っているせいです。

まずは代数の法則について説明します。

代数の法則とは

代数の法則を簡単に説明すると

という法則です。

もーっと簡単に説明すると

という内容になります。

コインを10回投げたとき、表の出た割合は50%から遠いかもしれません。

しかし、コインを1万回も投げれば表が出た割合は50%に非常に近くなっているのです。

これが「代数の法則」です。

「代数の法則」を間違って理解してしまう

代数の法則を「表が100回出たってことは裏も100回出るんだ！」と勘違いしてしまう人が非常に多い。本当に多い。

最大の勘違いを指摘します。

内容を理解できれば解決です！

さて、具体的に考えるためにコインを1万回投げてみました。

コインを投げた回数	表の数	表の出た割合	表と裏の出た回数の差
100回	45回	45.00%	10回
1000回	489回	48.90%	22回
10000回	4984回	49.84%	32回

コインを100回投げたときと10000回投げたときで表と裏の出た回数の差は広がっていますが、割合は50%に近づいています。

「確率は収束する」とは「表と裏の出る回数が同じになる」のではなく、「投げた回数が多くなるせいで割合にすると50%に近づく」という意味であり、表がたくさん出たから次は裏が出るだろ～という意味ではないのです。

ついでなのでグラフも用意しました。

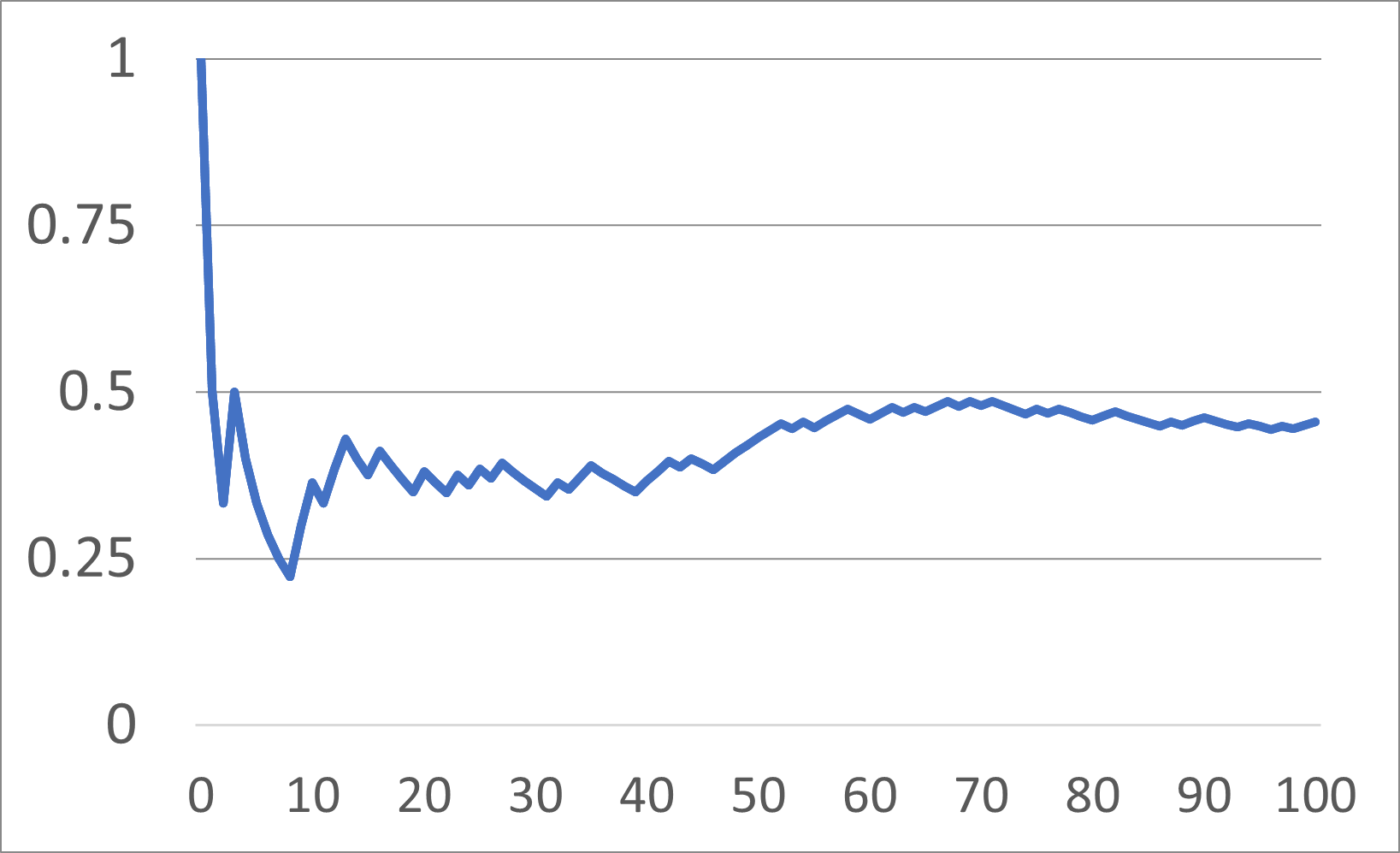
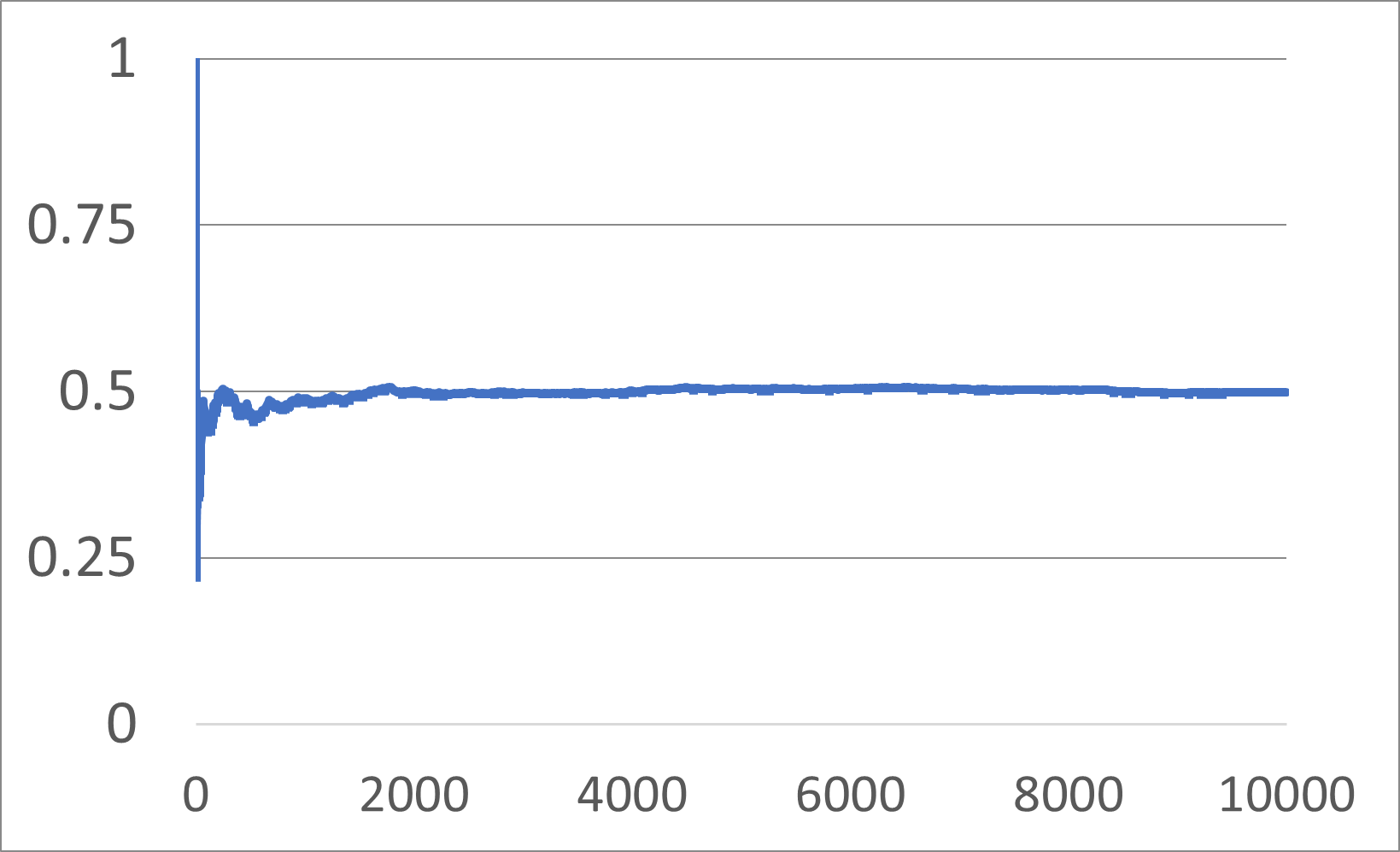
これが「確率は収束する」という具体例ですね。

「確率を収束させる」ためには確率母数の数百倍の試行回数が必要

そもそも、確率を収束させるためには確率分母の数百倍の試行回数が必要です。

500倍必要だとしても

は必要です。

まぁ大体300倍もあれば十分ですね。

日常生活におけるほとんどの場合、確率が収束するほどの試行回数に達することはまずないので、日常生活で確率が収束するようなことはほぼ何もありません。

誤用の原因その② 確率が独立していることを理解できていない

コインを投げて表の出る確率は\(\frac{1}{2}\)です。

当たり前のことを言っていますが、「表が連続して出てるしそろそろ裏も出るだろ～」と言っている人は、裏の出る確率が\(\frac{1}{2}\)よりも多いと心のどこかで思っているのではないでしょうか。

確率では、「前行った結果が次に影響しない」ことを独立と言います。

「コインで表が出たから次は裏が出る確率が高くなる」は、「コインで表が出たから次はサイコロで6が出やすくなる」と同じくらいキモいです。

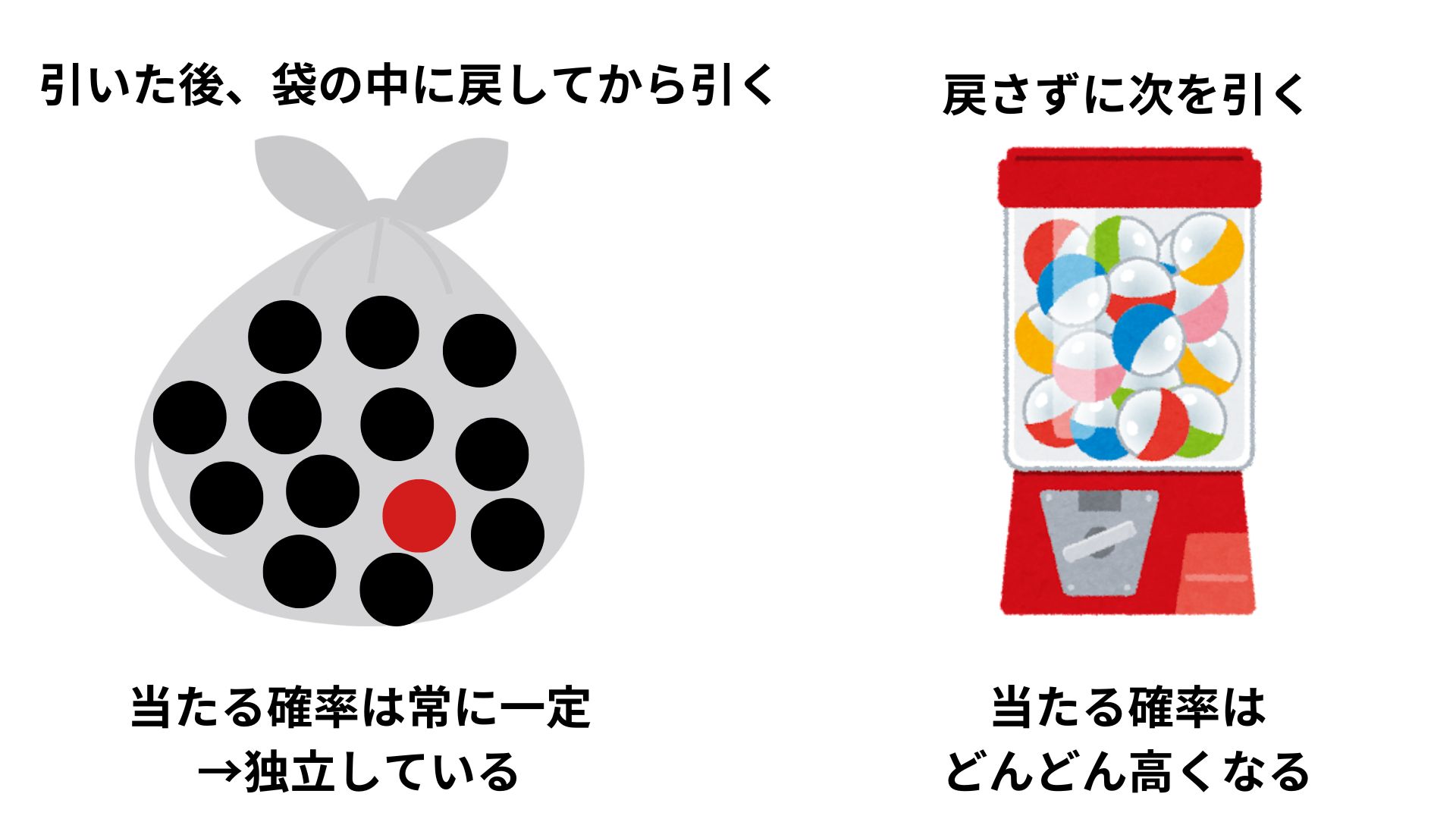
ガシャポンのような場合は、外れを引くことで母数が少なくなるので次に当たりやすくなり、独立していないと言えますね。

まとめ

「確率は収束する」は

また、

これらのことを理解して、「確率は収束する」を正しく使えるようになると良いですね！

以上です。