・圧力とは
・気圧と水圧とは
・浮力の公式の導出
物理には重力、張力、垂直抗力、弾性力などの力が登場しますが、これらの力以外にも様々な力が存在しています。
圧力は力ではないのですが、今回は色々な力の中でも「圧力と浮力」について説明していきます。
圧力とは
単位面積当たりにかかる垂直な力。
力を面積で割ったもの。
$$P=\frac{F}{S}$$
(F：力 S：面積)
圧力とは、単位面積当たりにはたらく垂直な力のことをいいます。
記号はPressure(プレッシャー)の頭文字であるPを使い、単位は［Pa］(パスカル)です。
単位面積(1m2のこと)当たりの力なので、力Fを面積Sで割ると圧力になります。(SはSurface areaの略です)
$$P=\frac{F}{S}$$
力を面積で割っているため、単位は［N/m2］なのですが、物理では［N/m2］のことを［Pa］と言います。
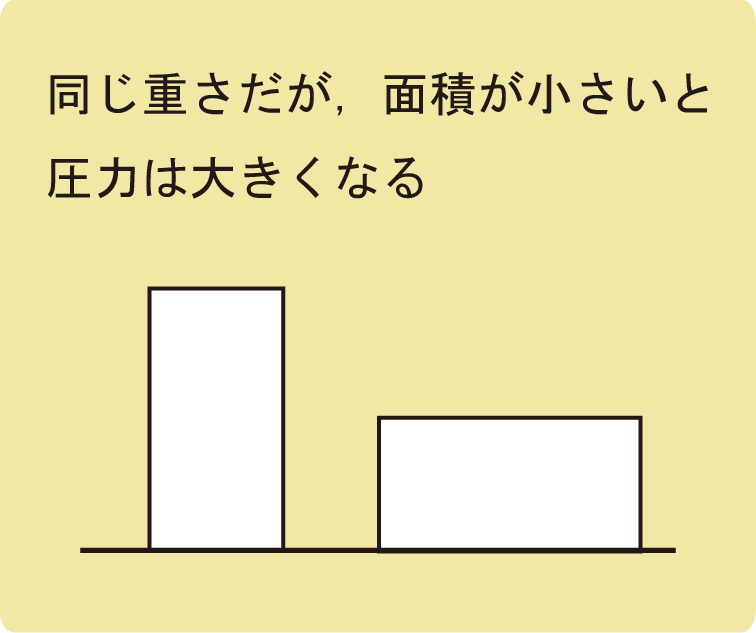
同じ重さのものであっても、面積が小さいと分母のSが小さくなるので、圧力が大きくなります。
箱を床に置いたとき、面積の大きい部分を下にすると、床にかかる圧力が少なくなるということを中学理科でも勉強しましたよね。
爪楊枝の尖っている部分は面積が非常に小さいため、圧力が大きくなり触ると痛いと感じます。
爪楊枝の尖っていない方を押したとしても痛くないのは、面積が大きくなると圧力が大きくなるからです。
試しに爪楊枝を50本くらい持って、尖っているところを手のひらに当ててみてください、全然痛みがなく、むしろ気持ちいいですよ。
このように、圧力には面積が関係しています。
圧力は力を面積で割ったものなので、圧力は「力」ではないということに注意
力の単位は［N］だが、圧力の単位は［Pa］
気圧とは
空気などの気体による圧力。
空気の重さを面積で割ったもの。
大気の圧力のことを大気圧といい、P0で表すことが多い。
P0＝1013hPa
気圧とは、空気などの気体による圧力のことをいいます。
圧力は力を面積で割ったものであり、気圧とは空気の重さを面積で割ったものとなるため、自分の頭上にある空気の量が気圧の大きさと関係しています。
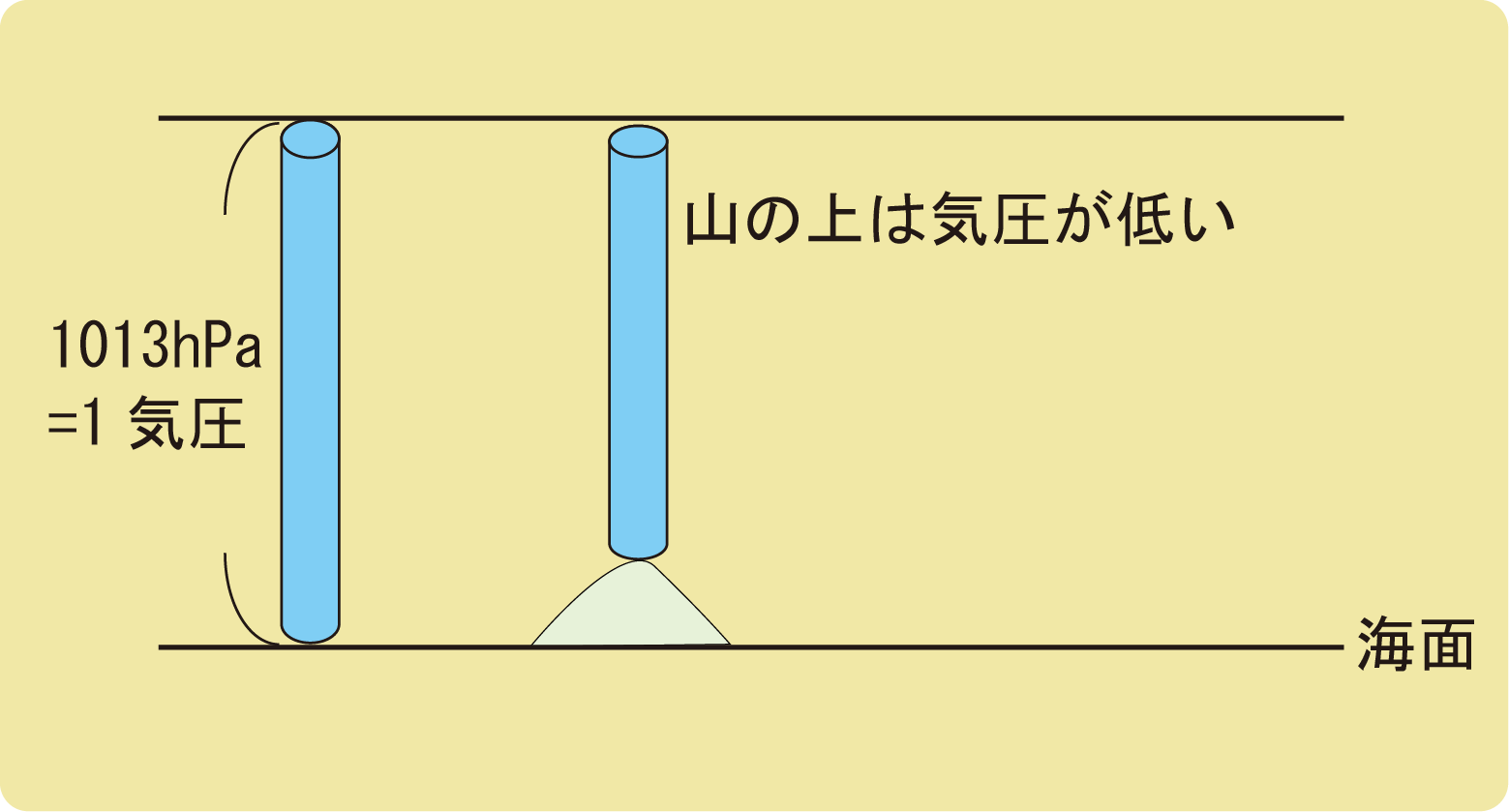
山の上では気圧が低くなるため、ポテチの袋が膨らんだり水が沸騰しやすかったりするということを聞いたことがあるのではないでしょうか。
山の上にいるということは、地上と比べると自分の上にある空気の量が少ないという事なので、気圧が低くなります。
また、天気でいうところの高気圧とは、空気がたくさん集まっているということになります。
1013hPaがパリ付近の平均的な海面での平均気圧となっているため、1013hPaのことを1気圧と言い、1つの基準となっています。
水圧とは
水による圧力。
水の重さを面積で割ったもの。
深ければ深いほど水圧は高くなり、海水10mが1気圧分の水圧となる。
$$P=P_0+ρhg$$
(P0 大気圧)
水圧とは、水による圧力のことをいいます。水の重さを面積で割ったものになるため、深ければ深いほど水圧は高くなります。
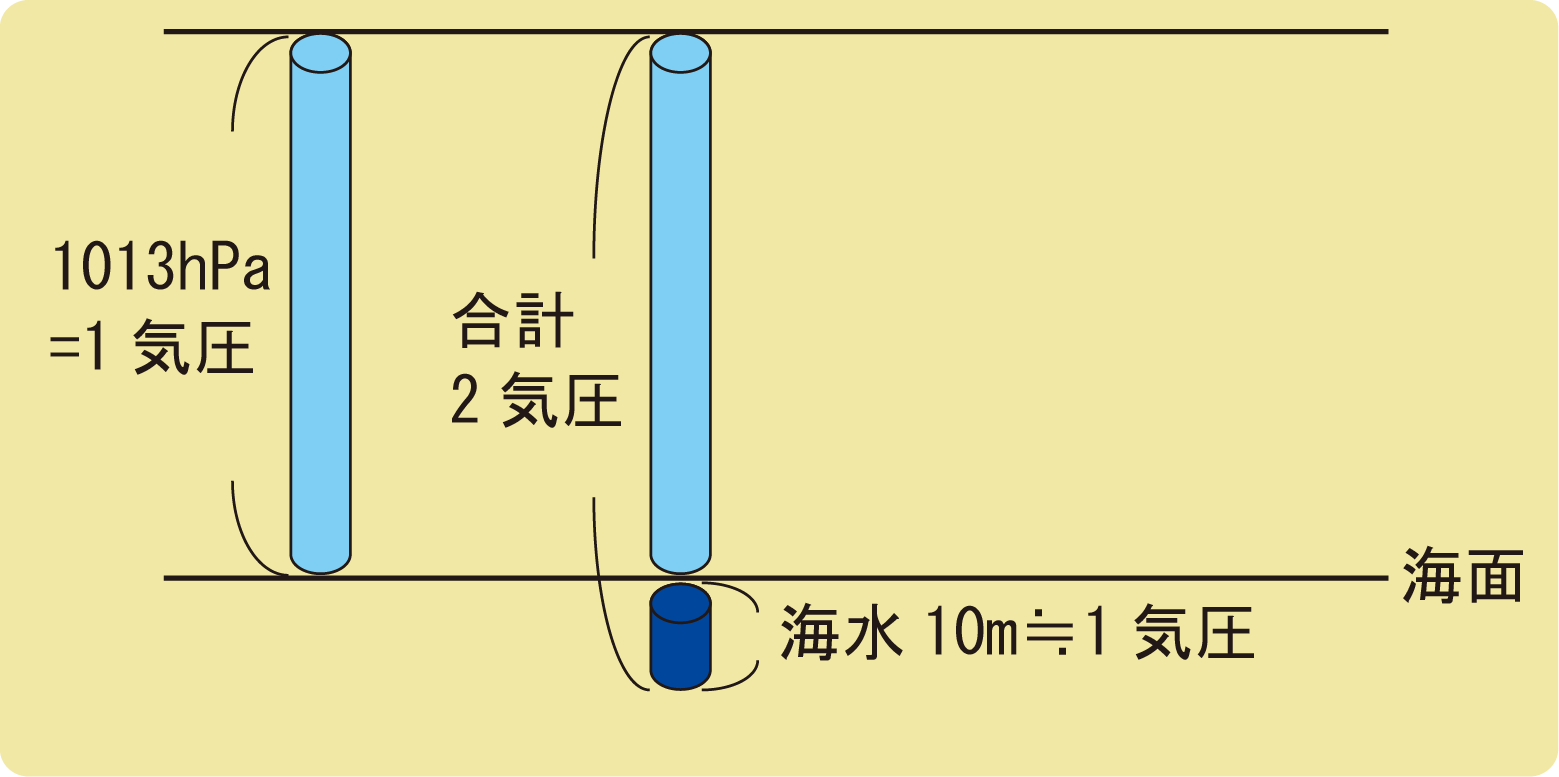
海水約10m分の圧力で1気圧と等しくなるので、10m潜ると2気圧の圧力を受けることになります。
海水の重さと大気の重さの両方の圧力が影響しているということです。
1m3あたりの質量。
$$ρ×V＝ｍ$$
(v：体積 m：質量)
になるので、水の場合は重さをmgではなくρVgで表す。
重さといえばmgですが、水の場合は質量ｍを使いません。
英語でいうところの不可算名詞のように、水の量はすぐに変わってしまうため、毎回質量を測ることをしないのです。
質量の代わりに、密度ρ(ロー) [kg/m3]と体積V[m3]を使います。ρ×Vで質量ｍになるので、水の密度をρとするとき水の重さはρVgとなります。(体積VはVolumeのVですね)
水圧は水の重さを面積で割ったものなので、水圧をPとすると
$$P=\frac{ρVg}{S}$$
体積V=面積S×高さｈなので、
$$P=ρhg$$
となり、大気圧P0とすると
$$P=P_0+ρhg$$
となります。
水の質量はmではなく、密度ρ×体積V⇒ρVを使います。
つまり、水の重さはmgではなくρVgです。
ρはローと読みます。ギリシャ文字です。
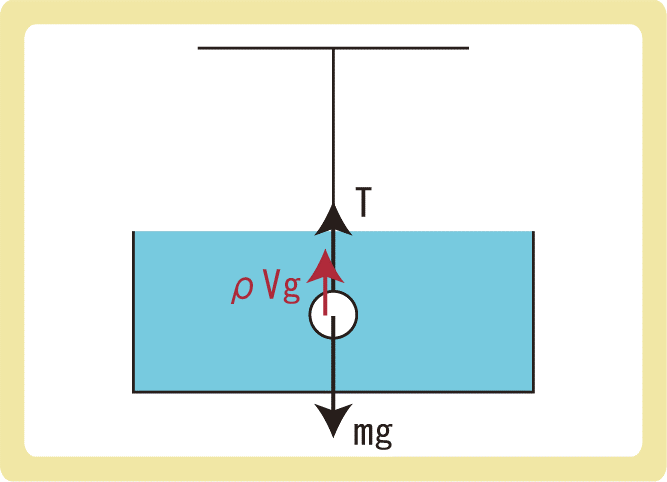
浮力とは
水や空気など、液体や気体の中にある物体が浮こうとする力
$$F=ρVg$$
浮力の大きさは、元々その場にあった液体や気体の重さと等しい。
浮力とは、水や空気などの液体や気体の中にある物体が浮こうとする力のことを言い、向きは重力と逆向きにはたらきます。
空気中でも浮力があるの？
と思うかもしれませんが、気球や風船が浮くのは浮力があるからですよね。
浮力の公式
$$F=ρVg$$
は、水圧の式から求めることができます。
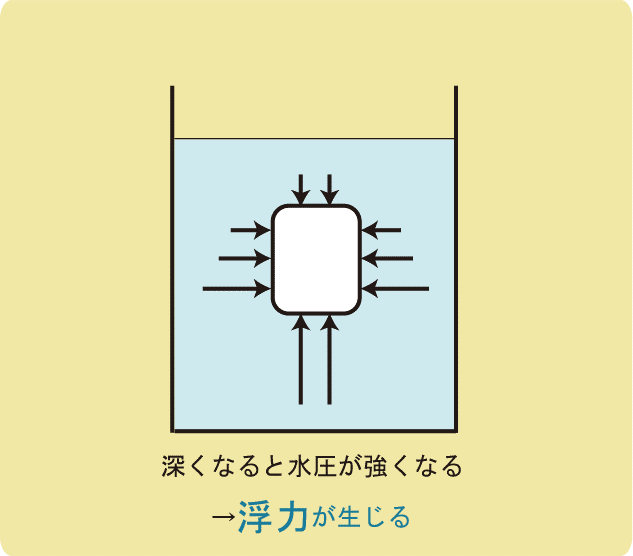
水圧は深くなればなるほど大きくなるのですが、ある程度の大きさを持つ物体を水の中に入れると、上面と下面の水圧に差が生まれ、その差が浮力となります。
（左右の水圧は同じ大きさなので、打ち消されます）
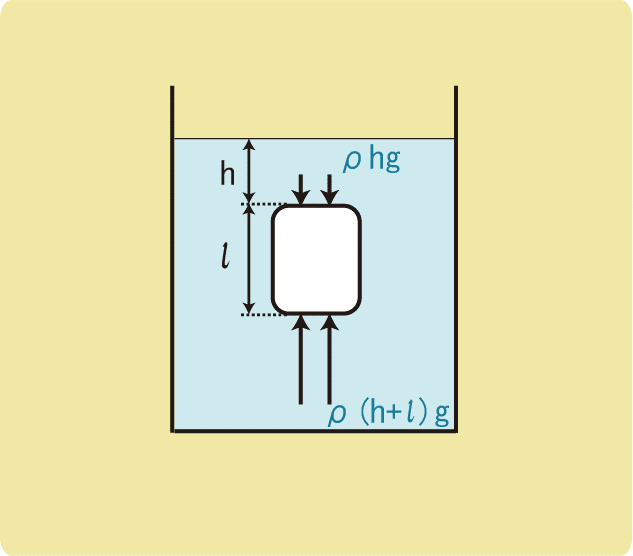
水圧の公式\(P=P_0+ρVg\)より
上面の水圧P1
$$P_1=P_0+ρhg$$
下面の水圧P2
$$P_2=P_0+ρ(h+l)g$$
となり、上向きをプラスとしたとき、その圧力の合計は
\begin{eqnarray}
P&=&-( P_0+ρhg)+ P_0+ρ(h+l)g\\
P&=&ρlg
\end{eqnarray}
となります。
ここで、圧力とは
$$P=\frac{F}{S}\\
F=PS$$
であるため、
\begin{eqnarray}
F&=&ρlg ×S\\
F&=&ρ(l×S)g\\
F&=&ρVg
\end{eqnarray}
となります。（\(体積V=面積S×高さl\)）
ρは水の密度であり、ρVで質量となるので、浮力ρVgは水の重さということになり、浮力の大きさは、元々その場にあった液体や気体の重さと等しいというアルキメデスの原理が成立します。
浮力は
$$F=ρVg$$
って覚えておけば大丈夫ですよ
ただし、ρは水の密度です。(油の中なら油の密度)
例題
例題1
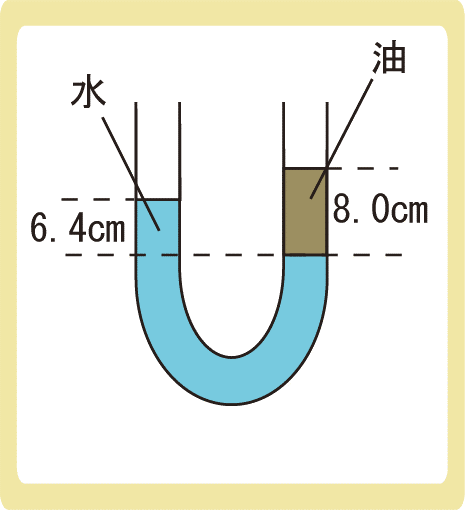
一様な太さのU字管に入れた油と水が図の位置でつりあっているとき、油の密度を求めなさい。ただし、水の密度ρ0=1.0×103kg/m3とする。
例題2
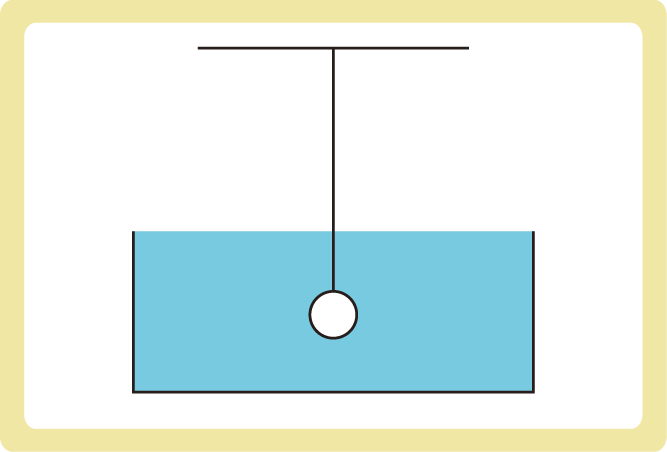
質量5.0kg、体積2.0×10-3m3の物体が糸に吊り下げられ水の中に入れられ静止している。以下の問に答えなさい。ただし、水の密度を1.0×103 kg/m3、重力加速度の大きさを9.8m/s2とする。
(1)物体にはたらいている浮力の大きさは何Nか。
(2)糸にはたらく張力の大きさは何Nか。
(1)浮力の大きさは
$$F=ρVg$$
を使い、求めます。
$$F=1.0×10^3×2.0×10^{-3}×9.8\\
F=2×9.8\\
F=19.6$$
∴19.6N
(2) 物体は静止しているので、力のつり合いを使います。
力のつり合いは、2つ先の回で詳しく勉強するので、この問題は後回しにしても大丈夫です。
まずは力を図示しましょう。
力のつり合いより
$$mg=T+ρVg$$
浮力は(1)の答えを使います。
$$5.0×9.8=T+19.6\\
T=49-19.6\\
T=29.4$$
∴29.4N
まとめ
圧力とは、力を面積で割ったものなので
$$P=\frac{F}{S}$$
です。
気圧は空気の圧力、水圧は液体の圧力であり、深くなればなるほど圧力は大きくなります。
水圧の差から、
$$F=ρVg$$
という公式を求めることができます。
・液体の中に物体が沈んでいるとき
・気球
などに浮力の公式を使います。
