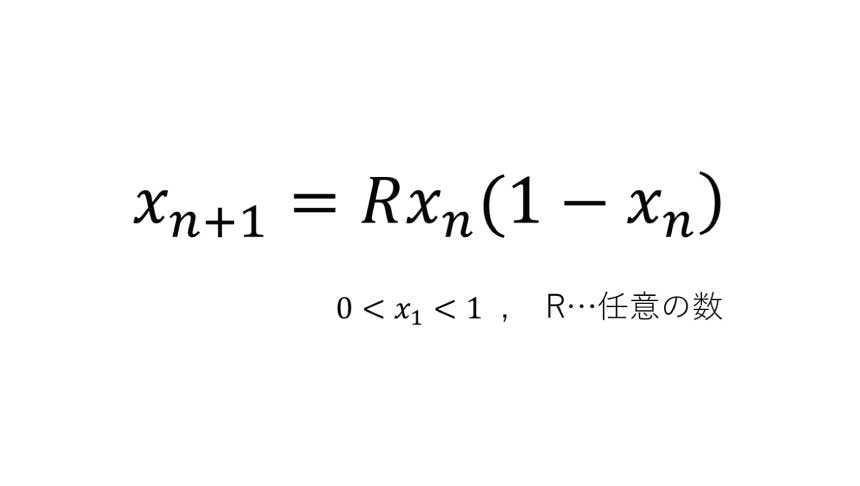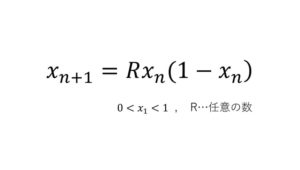ロジスティック写像の式とは何かご存知でしょうか。
「未来を完全に予知できるか?」
と聞かれたらあなたはどう答えますか?
「未来を完全に予知することは可能だ!!!」
その証拠は???
「未来を完全に予知することは不可能だ!!!」
その根拠は???
証拠や根拠とかを言われると困ってしまいますよね。
今回は、ロジスティック写像の式をわかりやすく解説し、未来は完全に予知することは不可能ということを説明しようと思います。
物理学と決定論
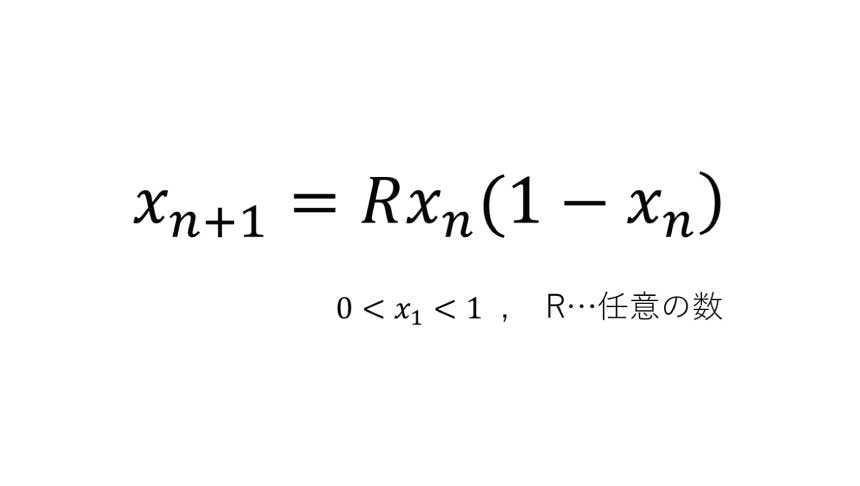
私は物理学をほんの少しだけ学んでいます。物理学という高い山があるとしたら、その麓には辿り着いたと言えるでしょう。
物理では
「ボールは何秒後に床に落ちるか」「この回路ではどれくらいの磁場が発生するか」「光はどう見えるのか」等々
色々な公式や微分方程式で未来予測をします。
物理を学び始めたばかりのときの自分は、人類が物理学を極めると未来のことを完全に予知できるようになるのではないか…?
と考えるようになっていました。
このような「未来は予め決まっている」という考え方を決定論と言います。
 男の子
男の子と考えている人でも
今から技術が更に発展した500年後の世界では、1か月先の天気までほぼ完璧に予知できていると思うか?
という問いに
「まぁ、可能性としてはあるのではないか?」
と考えてしまうor可能性があると思ってしまうのではないでしょうか。
予知と予測
「天気を完璧に予知することはできない」
と主張する人は、何日先までの天気ならばほぼ完璧に予知できると考えていますか?
明日の天気は絶対に晴れであると分かる場合でも、1週間後や2週間後の天気は分かりません。天気予報とは予測であり予知ではないので、あくまでも可能性の話をしていますよね。
「10年後の日本は〇〇になっている」
「50年後、世界人口は〇〇〇億人で打ち止めになる」
ということは全て予測であり予知ではありません。
(人口学者の人口予測を否定するつもりは全くありません。)
ただ、
予測も完璧ではなく、未来になればなるほど当たらなくなります。
そのことを数学と物理を用いて示していきます。
ロジスティック写像の式とは
ここで、ロジスティック写像の式というものを紹介します。
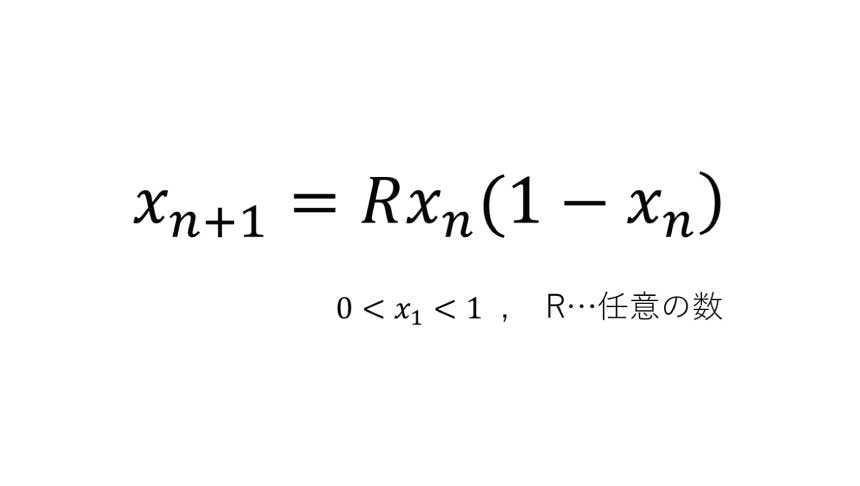
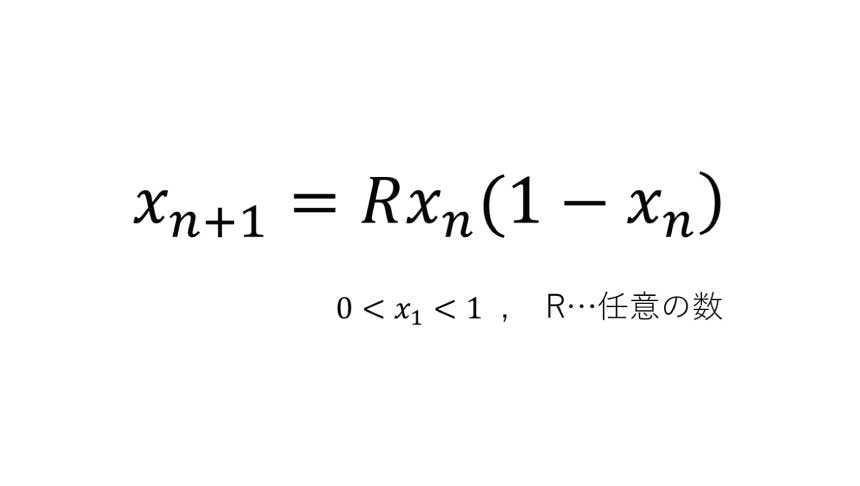
はい、これがロジスティック写像の式です。
数式を見た瞬間に「うわっ」と思った人も頑張って続きを読んで下さいね。
これは簡単な漸化式で、初項 $$x_1=0.5$$ で $$R=2$$ のとき、ロジスティック写像の式に代入すると $$x_2=0.5$$ となります。
ということは $$x_3=0.5$$ であり、永遠に0.5が続いていきます。グラフで表すとこうなります。
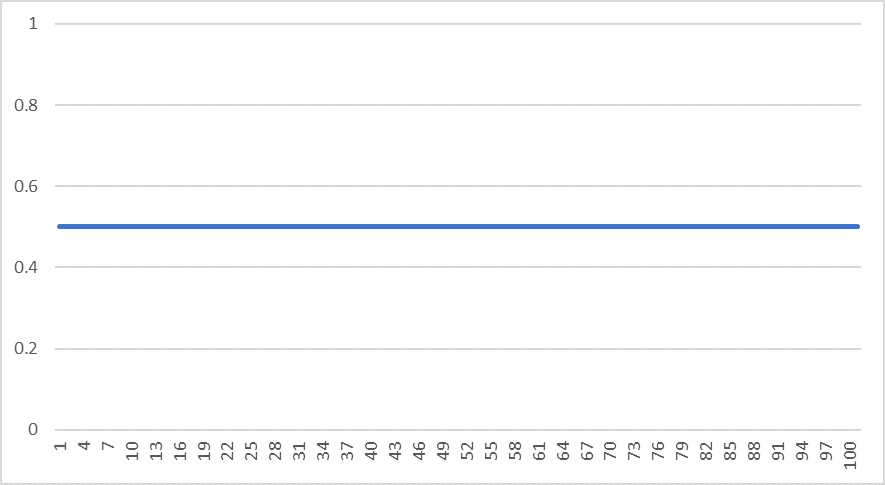

今度は$$x_1=0.6$$ で $$R=2$$に変更して、ロジスティック写像の式に代入して計算してみましょう。
そうするとグラフはこのようになります。

少し動きましたが、すぐ0.5に収束してしまいしたね。
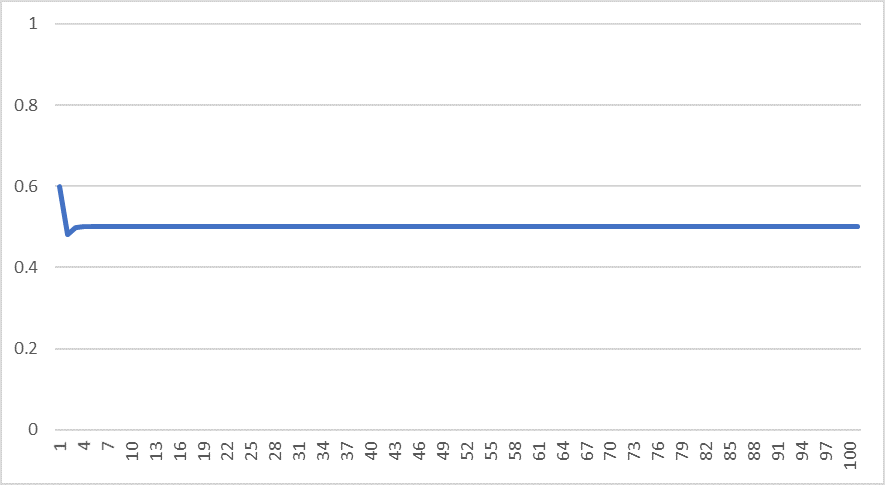
今度は$$x_1=0.9$$ $$R=2$$ にしてみましょう。

さっきよりは激しく動きましたが、すぐ0.5に収束してしまいました。
今度はRの値を変えてみます。
$$x_1=0.5$$ に戻し $$R=3$$にしてみましょう。
そうするとグラフはこんな形になります。
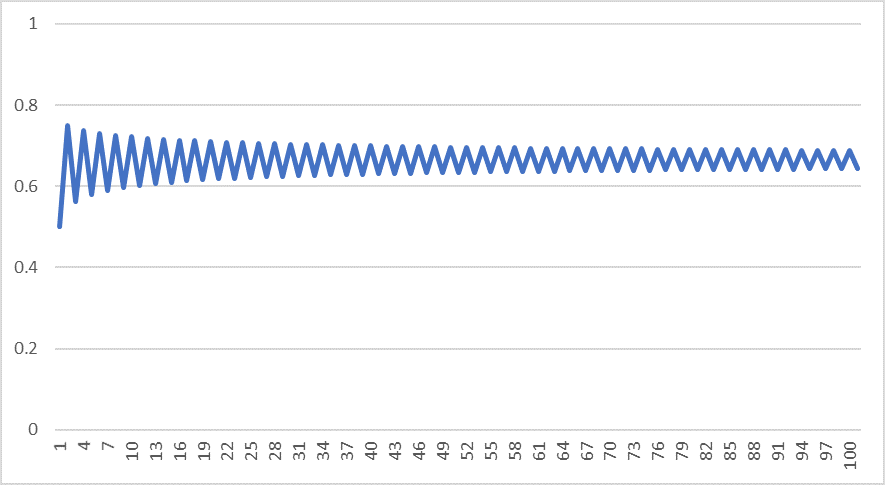

今度はグラフが収束せず振動のような動きをし始めました。
このように、Rの値を大きくしていくとグラフは変な動きをし始めます。
グラフの説明はこの辺として本題に入りましょう。
ロジスティック写像の式とカオス
ここからロジスティック写像の式の凄い所を説明していきます。
先程のように、今度は
$$x_1=0.5$$ のままにして $$R=3.8$$ にしてみます。
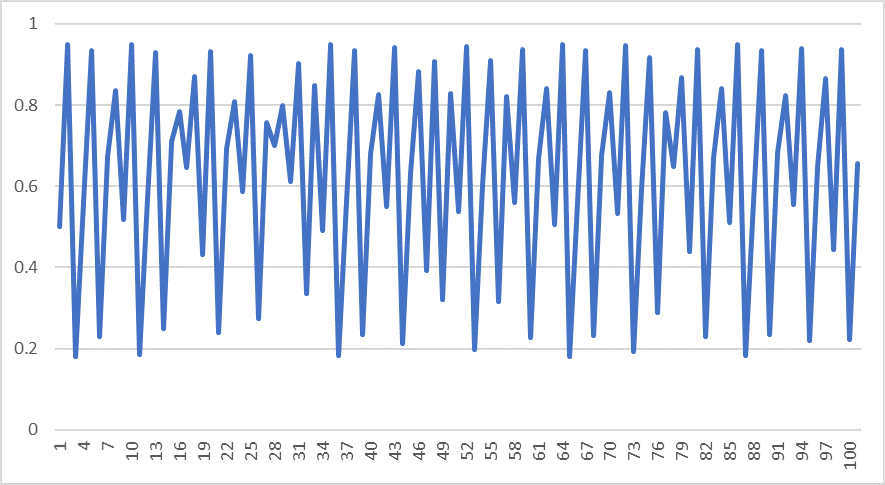

どんな法則の元に動いているのか分からなくなってしまいました。
一見ランダムに動いているように見えるので、疑似乱数として使えそうですね。カオスとも言えるでしょう。
一体これが何なのか?
と思った皆さん。
次に
$$x_1=0.500001$$ $$R=3.8$$ としてグラフを作ってみます。
※先程までの0.5は0.500000とします。違いが分からない人は気にしなくても大丈夫です。
では、グラフを見てみましょう。
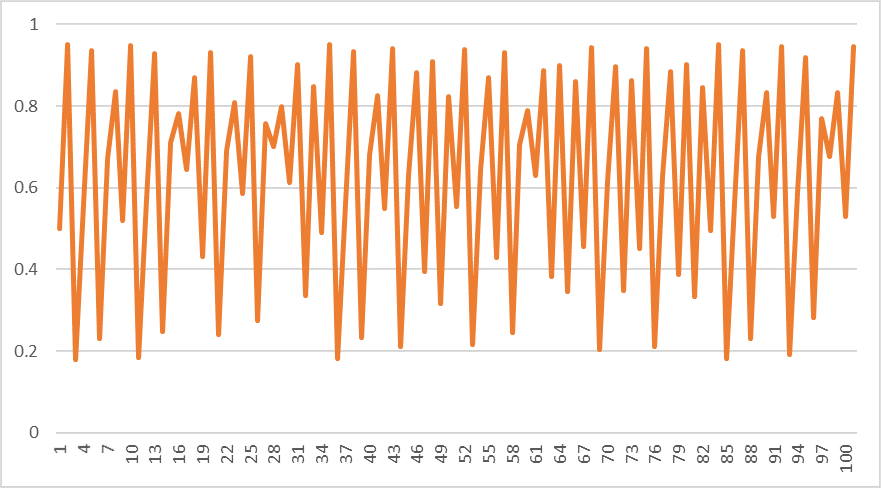

先程のグラフとの違いが分かりますか?
よーーーーーーく見て下さい。
違いが分かりましたか???
とっても分かりにくいと思うので、
グラフを重ねて見ることにします。
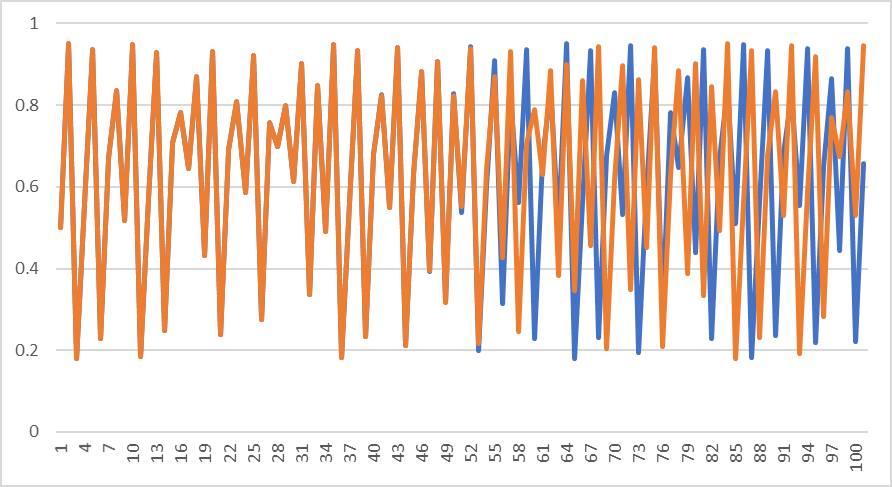

はい、こんな感じになります。
グラフを重ねると何が起こったのか一目瞭然ですよね。
最初の方はほぼ完全に同じ動きをしていたにも関わらず、ある程度進むと別の動きをし始めてしまいます。
これはどういうことかというと
初期条件が少しでも違うと未来は分からなくなる
ということです。
ダメ押しで、$$x_1=0.50000001$$ $$R=3.8$$ としてグラフを作ってみます。
そして、$$x_1=0.5$$ $$R=3.8$$ のグラフと比べてみましょう。
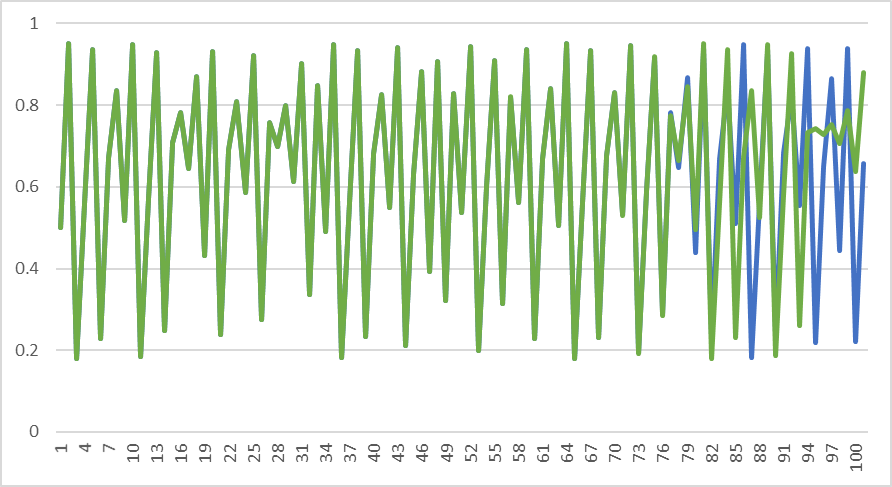

先程よりもグラフが一致している場所が多くなりました。
初期条件が詳しく分かっていれば分かっているほど未来を予測することが可能になるのです。
Excelを使えば簡単にグラフを作成することができるので、気になる人は個人的に作ってみてください。
条件が正しく分かっていないと未来は予測できない
天気予報も地震予知も無限に続く小数点を正しく分かっていないと完璧な未来予知は不可能です。
ロジスティック写像の式のよう、少しでも初期条件がズレてしまうと未来のことは分からなくなります。
「100年後の世界はこうなっている」
とテキトーに言うことは誰にでもできます。
人口学の専門家が世界人口は120億で停滞すると予測していることに納得していますが、かなり大雑把な数字にすることで的中率を上げているだけです。
10年以内にM8.0以上の地震が日本付近で起きる確率は〇〇%だ。というものは統計学の話であり、未来予知ではありません。
このまま技術が進化しても、1か月先の天気が正確に分かる時代はやってきません。
何事も初期条件が正しく分かっていないと未来は分からないのです。
じゃあ、初期条件が正しく分かれば未来は予測できるのか?
人類の技術で無理だとしても、もし宇宙の最初の状態を正確に把握できたら理論上未来予知ができるのか?
という問いがあったら、あなたはどう答えますか?
今回は長くなってしまったので、この疑問には別の機会で答えるとしましょう。
参考文献
今回参考にさせていただいた本です。
個人的に大好きな本です。複雑系の世界を覗くことができるので、理系学生にオススメの一冊です。
今回解説したロジスティック写像の式はもちろん、カオス理論における重要な考え方を養うことができる一冊となっています。