・空気抵抗とは
・終端速度とは
ただし、空気抵抗の影響はないものとする。
という文を、今まで何度も見てきましたよね。
物理では、空気抵抗を考えない場合が非常に多いのですが、この範囲では、もし空気抵抗がある場合はどうなるのかについて、少しだけ勉強をします。
それでは、空気抵抗がある場合の運動について、わかりやすく簡単に解説していきます。
空気抵抗とは
空気中を移動する物体にはたらく、運動を妨げる向きにはたらく力
物体の速度に比例するため、空気抵抗の大きさは\(f=kv\)と表される
(f:空気抵抗の大きさ[N] k:比例定数[kg/s] v:速さ[m/s])
空気抵抗とは、空気中を移動する物体にはたらく、運動を妨げる向きにはたらく力のことです。
物体が止まっているとき、空気抵抗はありません。物体が速く動けば早く動くほど空気抵抗は大きくなるため、
$$ f=kv$$
と表されます。
(速さの2乗以降の項も関係あるのですが、無視することが非常に多いです。また、比例定数\(k\)は物体の形や大きさによるのですが、高校物理では単純に\(k\)として考えます。)
例えば、高さ1000mの地点から雨粒が自由落下するときを考えます。
このとき、
$$v^2-{v_0}^2=2ax\\
v^2-0=2×9.8×1000\\
v=140$$
と計算できるので、雨粒は140m/sの速さで落下してくると考えることができます。
しかし、実際の雨粒の速さは、大きさにもよりますが速くても10m/sくらいです。
空気中を運動する物体は、空気抵抗の影響から速さが小さくなるのです。
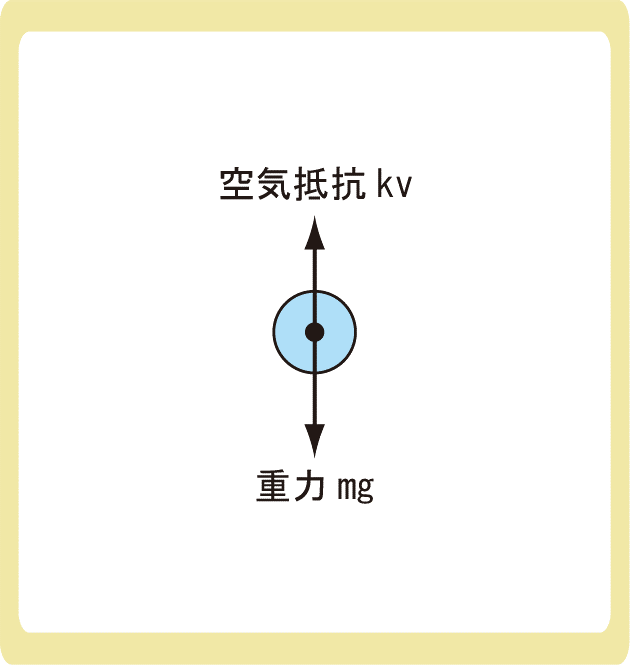
空気中を落下する雨粒にはたらく力は、重力と空気抵抗の2種類です。
運動方程式より、
$$ma=mg-kv$$
と式を作ることができます。
\(mg\)よりも\(kv\)が小さいとき、物体はどんどん加速していきますが、速くなると\(kv\)が大きくなるので、段々と加速しなくなっていきます。
最終的には\(mg\)と\(kv\)が同じ大きさになり、\(a=0\)となるので、速度は一定になります。このときの速度のことを終端速度といいます。
物体の速度が終端速度になっているとき、\(mg\)と\(kv\)はつり合っているため、終端速度は
$$mg=kv\\
v=\frac{mg}{k}$$
となります。
空気抵抗がないとき、落下する物体の速さに質量は関係ありません。
しかし、空気抵抗がある場合の終端速度は\(mg\)に比例するため、雨粒は大きければ大きいほど(質量が大きいほど)速く落下します。
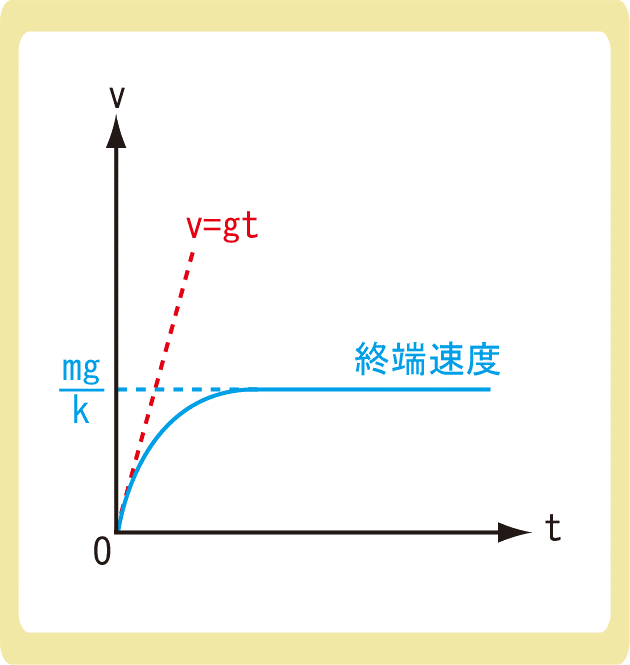
空気抵抗がなければ、上図の赤い線である\(v=gt\)のようにどんどん速くなりますが、空気抵抗の影響がある場合、物体の速度は一定の大きさになります。
まとめ
空気抵抗とは、空気中を移動する物体にはたらく、運動を妨げる向きにはたらく力のことです。
空気抵抗の大きさは速さに比例すると考え、空気抵抗の大きさ\(f\)は\(f=kv\)と表すことができます。
十分な時間が経った後、物体の速さは一定となり、そのときの速度のことを終端速度といいます。
物体が一定の速度で運動しているとき、空気抵抗と重力はつり合っていることになるため、
$$mg=kv$$
と式を作ることができます。












