・水平投射とは
・斜方投射とは
・モンキーハンティングについて
物理基礎では，物体を鉛直方向（重力のある方向）に投げた場合の運動について勉強しました。
自由落下・鉛直投げ下ろし・鉛直投げ上げは，水平投射と斜方投射の前提知識なので，落下運動についてしっかり覚えていない人は，まず復習からしてください。
今回は，水平投射と斜方投射について，わかりやすく簡単に解説をしていきます。
水平投射とは
物体を地面に対して水平方向に投げたときの運動
鉛直方向は自由落下，水平方向は等速直線運動になる
水平投射とは，物体を地面に対して水平方向に投げたときの運動のことです。
水平投射では，物体が直線ではなく放物線のように運動するので，分かりやすくするため鉛直方向と水平方向に分けて考えます。
物体に働く力は鉛直方向の重力のみであることと，水平方向に投げ出すため鉛直方向に初速度がないことから，鉛直方向は自由落下，水平方向は等速直線運動になります。
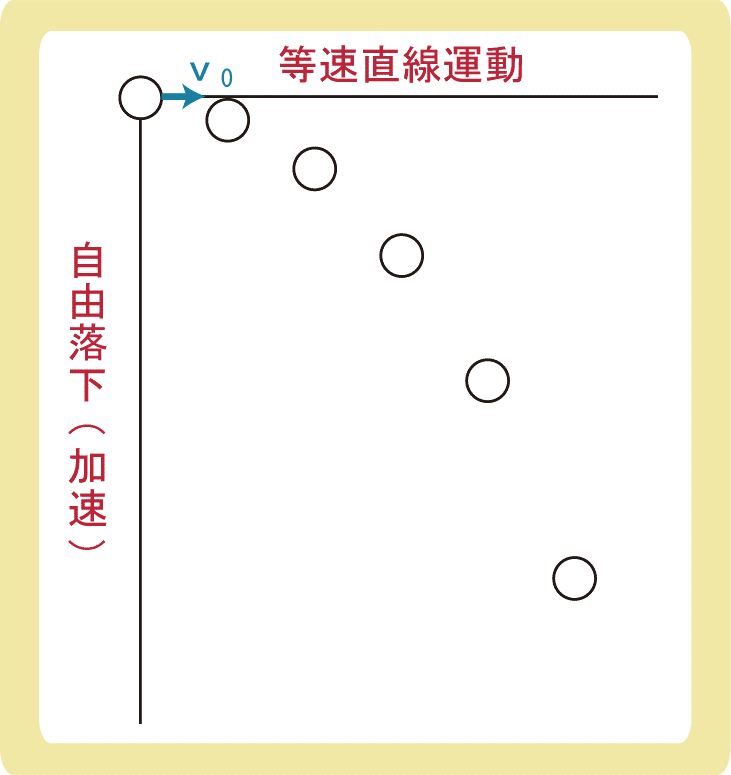
もちろん，落下するときの加速度は，重力加速度g［m/s2］になります。
鉛直方向は自由落下なので，使う公式は等加速度直線運動の公式と同じ
$$①v=v_0+at\\
②x=v_0t+\frac{1}{2}at^2\\
③v^2-{v_0}^2=2ax$$
です。
水平方向は等速直線運動なので，速度が一定であり，\(x=vt\)を使うことになります。
斜方投射とは
物体を斜め上に投げ上げる運動
鉛直方向は鉛直投げ上げ，水平方向は等速直線運動になる
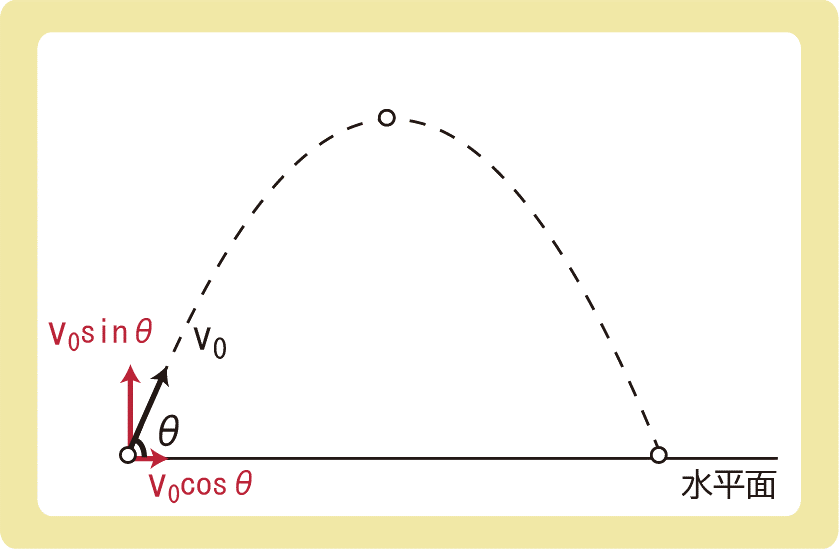
斜方投射とは，物体を斜め上に投げ上げる運動のことです。
水平投射と同様，物体は放物線のように運動するため，鉛直方向と水平方向に分けて考えると，働く力は重力のみであることと投げ上げていることから，鉛直方向は鉛直投げ上げ，水平方向は等速直線運動として考えることができます。
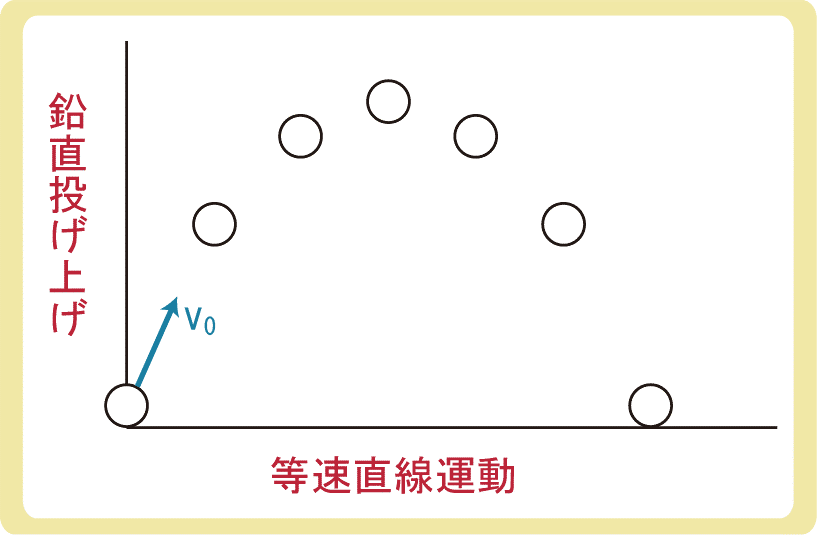
斜方投射は斜めに投げるので初速度も斜め向きになります。
平面上の運動では運動を上下左右に分解すると理解しやすいので，初速度も鉛直方向と水平方向に分解します。
水平方向からの角度をθとするとき，鉛直方向の初速度は\(v_0sinθ\)，水平方向の初速度は\(v_0cosθ\)となります。斜方投射を考えるときは，必ず初速度を分解しましょう。
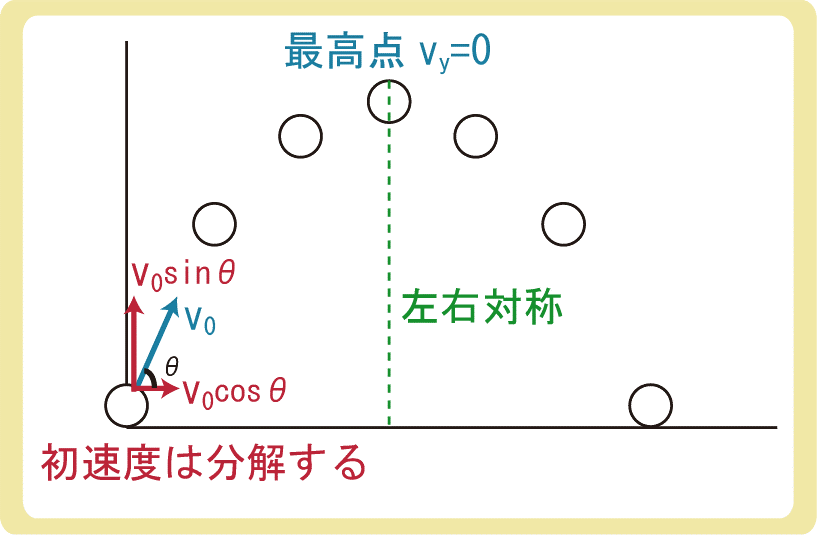
また，鉛直方向は鉛直投げ上げなので，最高点では鉛直方向の速度が0となります。速度が0ではなく，鉛直方向の速度が0です。水平方向には動いています。
さらに，最高点の軸を中心に左右対称になるので，最高点に上がるまでにかかる時間と最高点から落ちるために必要な時間が等しくなったり，同じ高さでは速度の大きさが等しくなったりします。
例題
例題1
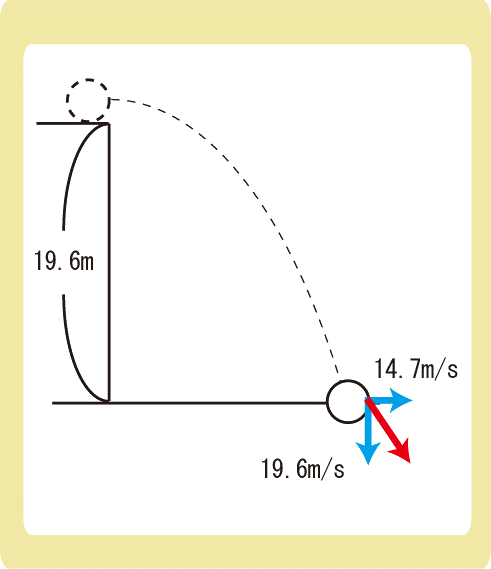
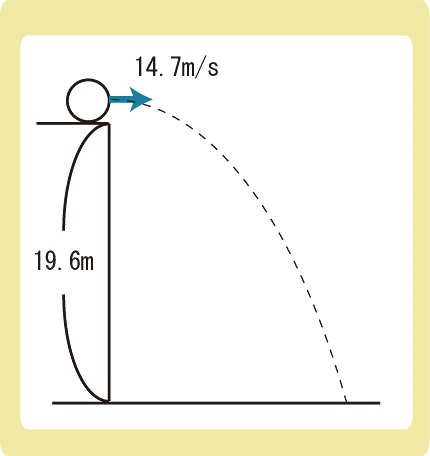
地面からの高さが19.6mのところから，小球を水平に14.7m/sで投げた。重力加速度の大きさを9.8m/s2として，次の各問に答えなさい。
(1)小球が地面に達するのに何秒かかるか。
(2)小球が地面に達したとき，小球を投げた場所から何m先まで進んでいるか。
(3)小球が地面に達したときの小球の速さを求めよ。
水平投射や斜方投射の問題を解くときは，水平方向と鉛直方向を分けて考えます。
水平投射は，水平方向が等速直線運動，鉛直方向が自由落下です。
(1)小球が地面に落ちるまでの時間を考えればよいので，鉛直方向を考えます。
鉛直方向は自由落下なので，19.6mの高さから小球を自由落下させる問題と同じです。
$$\begin{eqnarray}x&=&v_0t+\frac{1}{2}at^2\\
19.6&=&0+\frac{1}{2}×9.8×t^2\\
t^2&=&4\\
t&=&2\end{eqnarray}$$
∴2秒
(2) (1)より，小球が地面に達するのに2秒かかることが分かっているので，小球は2秒間進んだことになります。
水平方向は等速直線運動なので，単純に，速さ×時間が進んだ距離です。
$$x=14.7×2\\
x=29.4$$
∴29.4m
(3)地面に達したときの速さとは，水平方向でも鉛直方向でもなく，斜め方向の速さのことを指しています。
斜め方向の速さを求めるためには，地面に達したときの水平方向と鉛直方向の速さを求め，三平方の定理等を使えばよいです。
水平方向は等速直線運動なので，速さは14.7m/sのままです。
鉛直方向は自由落下なので，t=2秒を使って
$$v=v_0+at\\
v=0+9.8×2\\
v=19.6$$
と求めます。
あとは，14.7と19.6を用いて三平方の定理を使えばよいのですが，14.7と19.6はそれぞれ4.9×3と4.9×4であり，3：4：5の三角形であることが分かるので，
$$4.9×5=24.5$$
∴24.5m/s
例題2
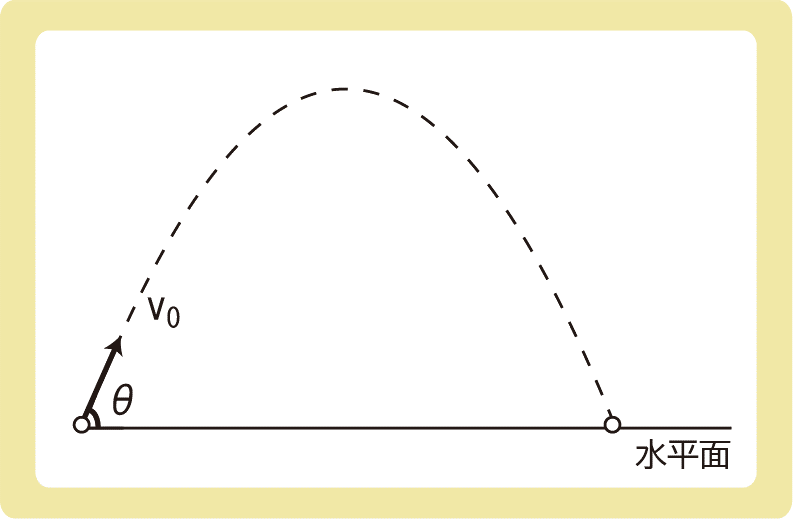
水平な地面から，水平方向と角θをなす向きに初速度\(v_0\)で物体を投げ上げた。重力加速度の大きさを\(g\)として，次の各問に答えなさい。
(1)最高点に達するまでにかかる時間を求めよ。
(2)最高点の高さを求めよ。
(3)地面に達するまでにかかる時間を求めよ。
(4)水平到達距離を求めよ。
(5)初速度が一定のとき，水平到達距離が最大になるようなθの値を求めよ。
斜方投射では，まず，初速度を水平方向と鉛直方向に分解します。
文字式のみの問題では，問題文にある文字のみを使って解答しなければいけません。
今回であれば，\(v_0\)，\(θ\)，\(g\)以外の文字は，解答に使えないので注意しましょう。
(1)最高点に達するまでにかかる時間を\(t_1\)とします。
\(t_1\)を求めるために鉛直方向のみを考えると鉛直投げ上げになるので，
「初速度\(v_0sinθ\)の物体を投げ上げたときの最高点までにかかる時間を求める」
という物理基礎の問題と同じになります。
$$v=v_0+at\\
0=v_0sinθ-gt_1\\
t_1=\frac{v_0sinθ}{g}$$
∴\(\frac{v_0sinθ}{g}\)
(2) (1)と同様，鉛直方向を考えます。
最高点の高さを\(h\)とすると
h&=&v_0sin×t_1-\frac{1}{2}×g×{t_1}^2\\
h&=&v_0sin×\frac{v_0sinθ}{g}-\frac{1}{2}×g×({\frac{v_0sinθ}{g}})^2\\
h&=&\frac{{v_0}^2{sinθ}^2}{g}-\frac{{v_0}^2{sinθ}^2}{2g}\\
h&=&\frac{{v_0}^2{sinθ}^2}{2g}\end{eqnarray}$$
∴\(\frac{{v_0}^2{sinθ}^2}{2g}\)
(3) 斜方投射では，対称性を用いることで簡単に問題を解くことができます。
地面に達するまでにかかる時間を\(t_2\)とすると，\(t_2\)は\(t_1\)の2倍になるので，
$$\begin{eqnarray}t_2&=&t_1×2\\
t_2&=&\frac{v_0sinθ}{g}×2\\
t_2&=&\frac{2v_0sinθ}{g}\end{eqnarray}$$
∴\(\frac{2v_0sinθ}{g}\)
(4)水平到達距離を求めるためには，水平方向を考えます。
水平方向は等速直線運動なので，単純に，速さ×時間が距離となります。
水平到達距離を\(l\)とすると
$$\begin{eqnarray}l&=&v_0cosθ×t_2\\
l&=&v_0cosθ×\frac{2v_0sinθ}{g}\\
l&=&\frac{2v_0^2sinθcosθ}{g}\end{eqnarray}$$
∴\(\frac{2v_0^2sinθcosθ}{g}\)
(5) (4)で，水平到達距離が\(l=\frac{2v_0^2sinθcosθ}{g}\)であると分かりました。
初速度\(v_0\)が一定のとき，\(l\)が最大になるようなθの値は何か，という問題です。
この問題を解くためには，数Ⅱの三角関数の範囲で勉強する，加法定理を使わなければなりません。
$$sin2θ=2sinθcosθ$$
という公式を知っていますか？
この公式を使うことで，
$$\begin{eqnarray}l&=&\frac{2v_0^2sinθcosθ}{g}\\
l&=&\frac{v_0^2sin2θ}{g}\end{eqnarray}\\$$
とすることができます。
問題より\(v_0\)が一定であり，もちろん\(g\)も一定なので，\(sin2θ\)が最大になるようなθを求めます。
\(2θ=90°\)のときに\(sin2θ\)は最大値の1となるので，\(θ=45°\)となります。
∴45°
例題3 (モンキーハンティング)
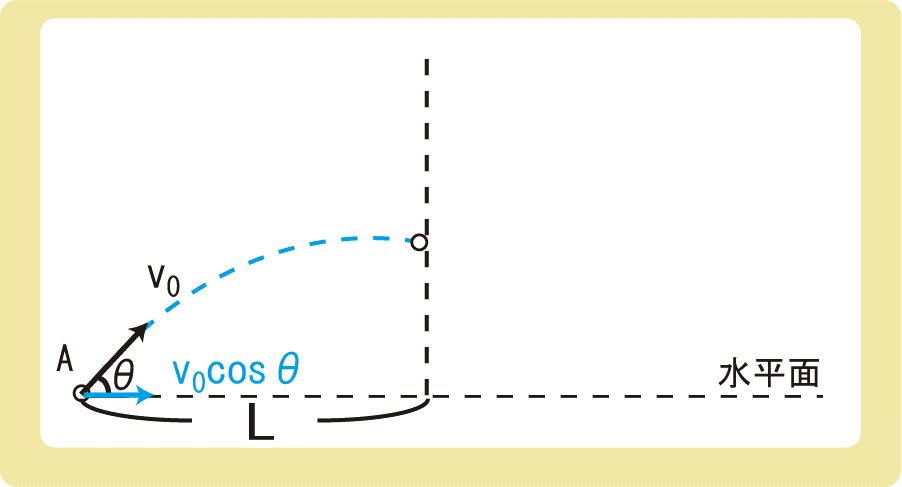
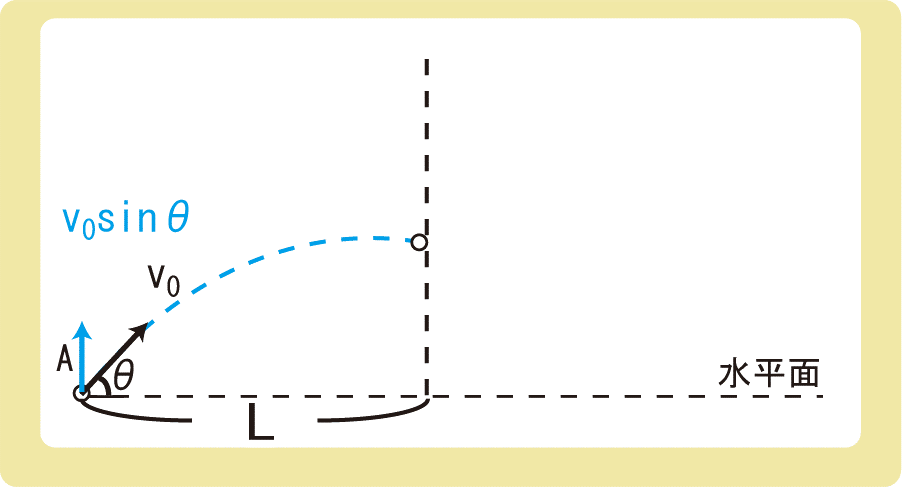
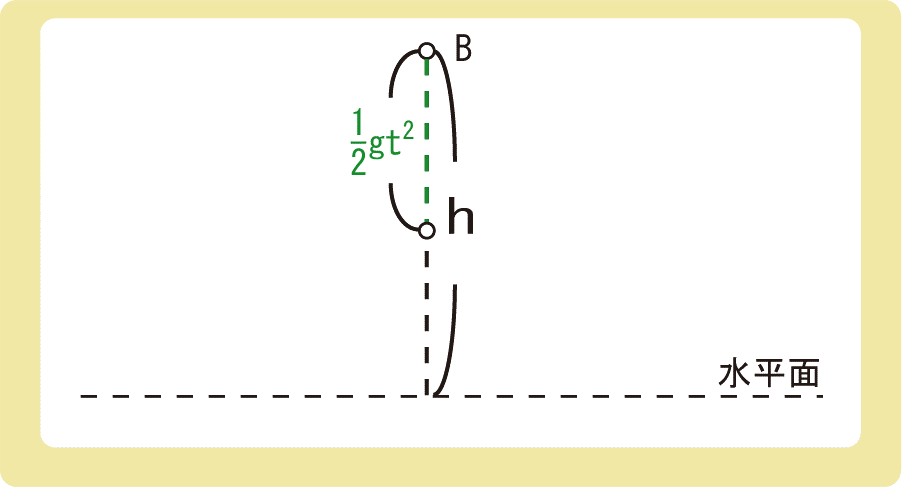
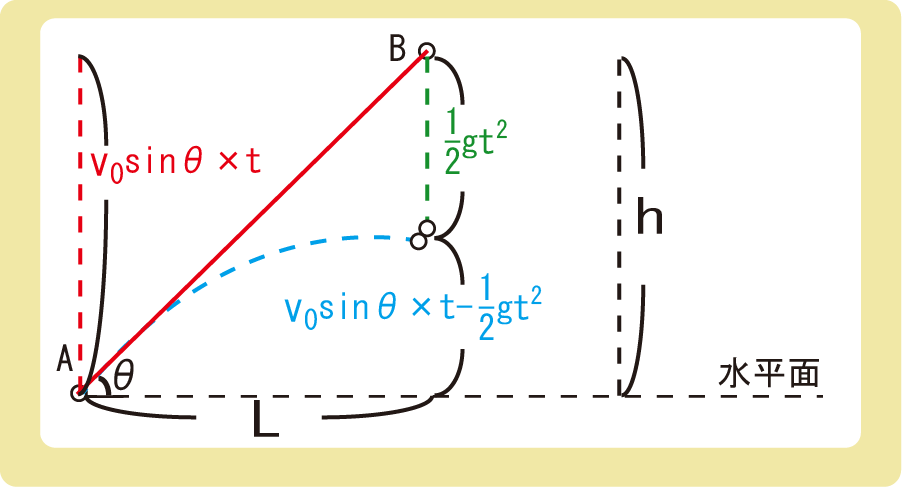
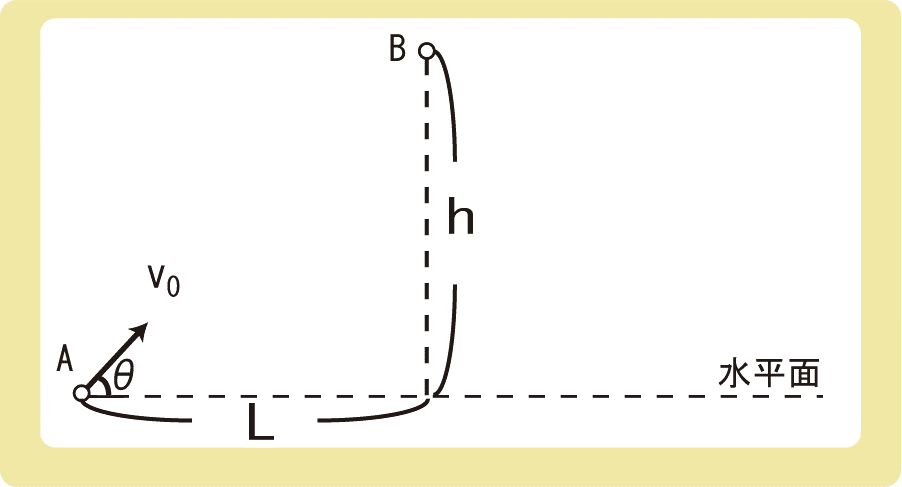
下図のように，時刻t=0に物体Aを仰角θ，初速度の大きさv0で投げ出すのと同時に，物体Bを自由落下させた。物体AとB間の水平方向の長さをL，鉛直方向の長さをhとするとき，以下の問いに答えなさい。ただし，重力加速度の大きさをgとする。
(1)物体AがLだけ進んだときの時刻を求めよ。
(2)(1)の時刻における物体Aの水平面からの高さを求めよ。
(3) (1)の時刻における物体Bの水平面からの高さを求めよ。
(4) (1)の時刻において，物体Aと物体Bが衝突するためのθの条件を求めよ。
普通の斜方投射の問題，普通の自由落下の問題だと思い，(1)～(3)を解きましょう。
(1)
初速度の水平成分は\(v_0cosθ\)であり，水平方向は等速直線運動なので，
$$L=v_0cosθ×t\\
t=\frac{L}{v_0cosθ}$$
∴\(\frac{L}{v_0cosθ}\)
(2)(1)で求めたtを，\(x=v_0t+\frac{1}{2}at^2\)に代入します。
もちろん，鉛直方向は鉛直投げ上げであり，加速度が\(-g\)になることに注意しましょう。
x_A&=&v_0sinθ×\frac{L}{v_0cosθ}-\frac{1}{2}×g×\frac{L^2}{{v_0}^2cos^2θ}\\
x_A&=&Ltanθ-\frac{gL^2}{2{v_0}^2cos^2θ}\end{eqnarray}$$
∴\(Ltanθ-\frac{gL^2}{2{v_0}^2cos^2θ}\)
(3) (2)と同様，(1)で求めたtを，\(x=v_0t+\frac{1}{2}at^2\)に代入します。
物体Bは自由落下するため，初速度は0です。
$$\begin{eqnarray}x&=&v_0t+\frac{1}{2}at^2\\
x_B’&=&0+\frac{1}{2}×g×\frac{L^2}{{v_0}^2cos^2θ}\\
x_B’&=&\frac{gL^2}{2{v_0}^2cos^2θ}\end{eqnarray}$$
水平面からの高さを求めるため，上図のように考えると水平面からの高さは\(h-x_B’\)となり，
$$x_B=h-x_B’\\
x_B=h-\frac{gL^2}{2{v_0}^2cos^2θ}$$
∴\(h-\frac{gL^2}{2{v_0}^2cos^2θ}\)
(4)物体Aと物体Bが衝突するためには，(1)の時刻において，物体Aの高さと物体Bの高さが等しければ良いと考えます。
$$x_A=x_B$$
tanθ=\frac{h}{L}$$
∴\(tanθ=\frac{h}{L}\)
\(tanθ=\frac{h}{L}\)で重力がないとき，物体Aは上図の赤線の向きに飛んでいきます。
このとき，物体Aは等速直線運動をするため，速さ×時間より，水平面からの高さは\(v_0sinθ×t\)となり，物体Bは自由落下するため，t秒で進む距離は上図の通り\(\frac{1}{2}gt^2\)となります。
この\(v_0sinθ×t\)と\(\frac{1}{2}gt^2\)は，等加速度直線運動の公式\(x=v_0t+\frac{1}{2}at^2\)と非常に似ていることに気づきましたか？
実際，上図の通り，重力がある場合の高さは\(v_0sinθ×t-\frac{1}{2}gt^2\)となり，上の2つと関りの深いことが明確です。
\(v_0sinθ×t-\frac{1}{2}gt^2\)は，等速直線運動しながら自由落下していると考えることができるため，\(taanθ=\frac{h}{L}\)(物体Bに向けて投げる)とき，物体Aと物体Bが衝突するのです。
物体Aが弾丸，物体Bが猿であるとします。
弾丸を発射すると，弾丸の発射と同時に，猿は発射音に驚いて自由落下してしまうと考えます。
このとき，猿の落下について深く考えずとも，猿をめがけて弾丸を発射することで，弾丸を猿に命中させることができます。
このような例から，上のような問題をモンキーハンティングといいます。
まとめ
水平投射と斜方投射は，落下運動を平面で考えた運動です。
水平投射は，自由落下＋等速直線運動
斜方投射は，鉛直投げ上げ＋等速直線運動
なので，物理基礎の範囲でもある自由落下・鉛直投げ下ろし・鉛直投げ上げを理解していないと，問題を解くことはできません。
水平投射よりも斜方投射の問題の方が豊富なバリエーションを持つため，応用問題はほとんど斜方投射の問題となります。
