・質点と剛体の違い
・力のモーメントとは
・剛体のつり合いの問題の解き方
物理基礎では，物体の大きさや形を考えませんでした。
物体を横に引っ張ったとき，物体は横に動くかもしれませんが，もしかしたら回転するかもしれません。
今回は，力のモーメントという「物体を回転させる力の性質」について，わかりやすく簡単に解説していきます。
質点と剛体の違い
大きさも形もない質量のある点
大きさと形のある変形しない質量のある物体
質点とは，大きさも形もない質量のある点のことをいいます。
一方，剛体とは，大きさと形のある変形しない質量のある物体のことをいいます。
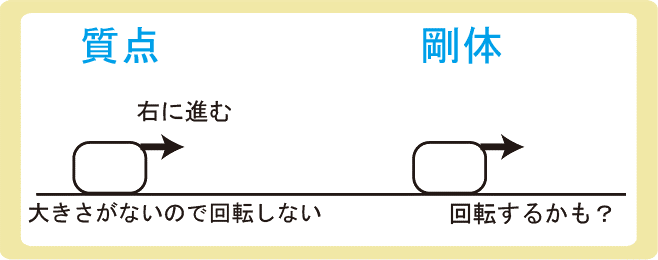
物理基礎では，物体の大きさや形を考えませんでした。
物体を横に引っ張るとき物体は単純に横に進むと考えていましたが，形や大きさ等を考えると横に進むのではなく回転するかもしれません。
剛体のつり合いや重心の範囲では，物体に形があり，力を受ける場所によっては回転するかもしれないということを考えていきます。
力のモーメント
物体を回転させようとする作用の量
$$M=F×l$$
(M：力のモーメント［N・ｍ］ F：力の大きさ［N］ l：軸からの長さ［m］)
力のモーメントとは，物体を回転させようとする作用の量のことです。
力のモーメントの単位は［N・m］であるため，力ではありませんが，物体を回転させる”回転力”というイメージを持つと良いでしょう。
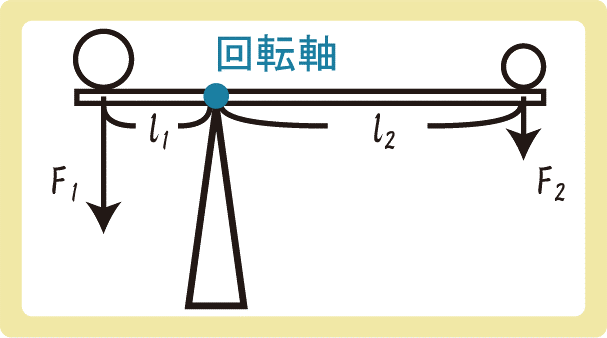
上図のような軽い（質量を無視できる）剛体の棒を用意します。
両側におもりを乗せて棒を回転させようとしたところ，棒は回転しませんでした。
てこの原理を考えると，このとき棒にはたらく関係式は
$$F_1l_1=F_2l_2$$
となり，これが力のモーメントを表す式となります。
つまり，力のモーメントの大きさは力の大きさ×腕の長さ（回転軸からの距離）ということです。
力が大きければ大きいほど回転しやすくなり，力のはたらく位置が回転軸から遠くなれば遠くなるほど回転しやすくなります。
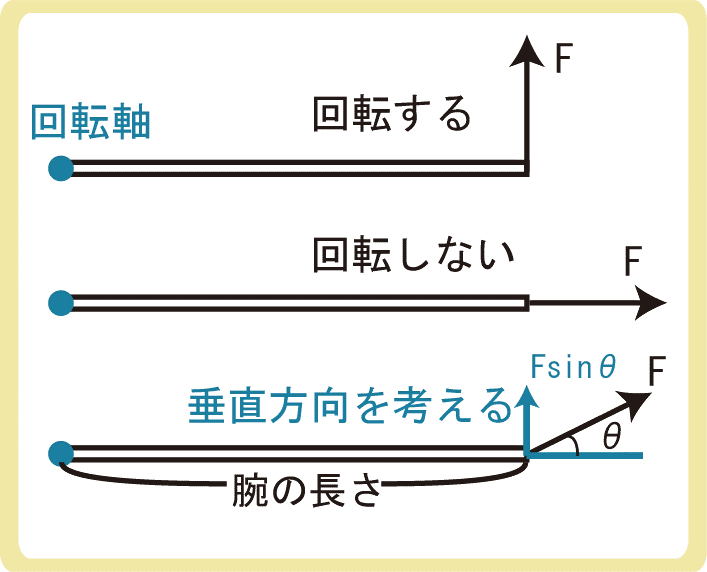
力の向きに気をつける必要があります。。
力の向きは腕に対して垂直でなければなりません。回転軸に対して平行に力をはたらかせても物体は回転しないのです。
もちろん，腕に対して斜めにはたらいている力の場合は，力を分解して垂直成分だけ取り出します。
例題
例題1
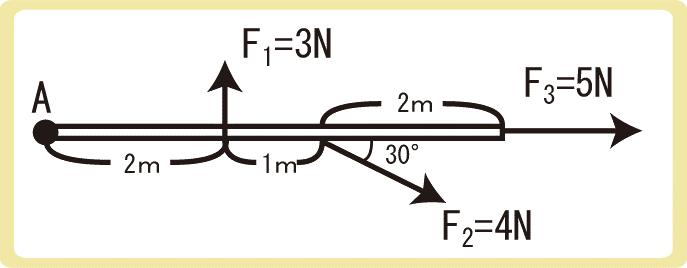
点Aまわりの力のモーメントM1～M3を，F1～F3についてそれぞれ求めよ。ただし，反時計回りを正とする。
剛体のつり合い
力の和が0，かつ，力のモーメントの和が0の状態のこと
力の和が0，かつ，力のモーメントの和が0の状態のことを，剛体のつり合いといいます。
物理基礎では，力がつりあっている物体は動かない(もしくは等速直線運動のまま)と考えていました。
しかし，形や大きさのある剛体では，力がつりあっていても動いてしまうかもしれません。
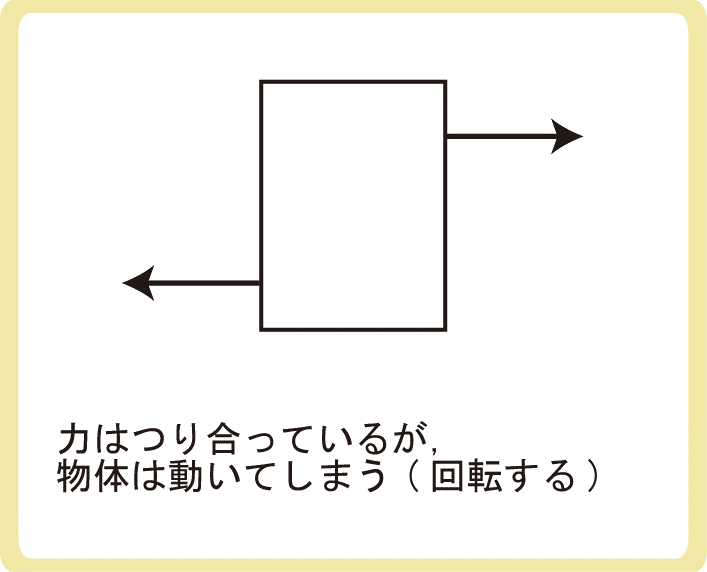
剛体を静止させるには，力がつりあっているだけではなく，力のモーメントの和も0(このサイトでは「力のモーメントがつり合っている」と呼ぶことにします)，つまり，回転しないことも条件に加える必要があります。
力もつり合っていて，力のモーメントもつり合っているとき，剛体がつり合っていると考えるのです。
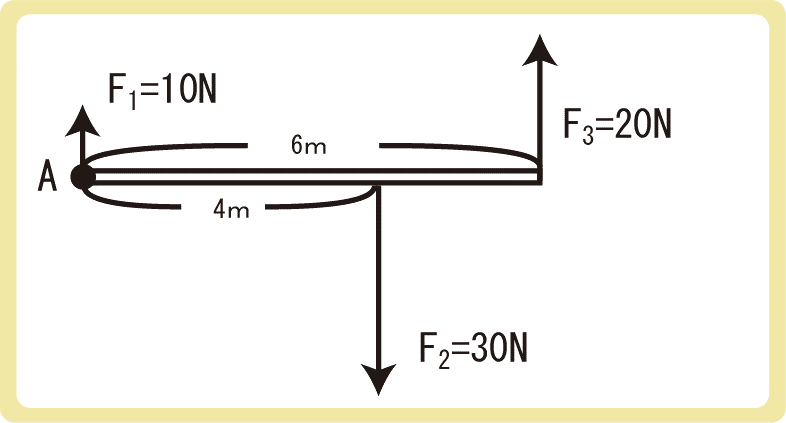
上図のような軽い（質量を無視できる）剛体にはたらく力を考えます。
上向きに働く力の大きさの合計：30N（10＋20）
下向きに働く力の大きさの合計：30N
上向きの合力＝下向きの合力なので，力がつり合っています。
次に，点Aまわりの力のモーメントについても考えます。まず，F1は回転軸にはたらく力なので，F1による力のモーメントは0 N・mになります。回転軸Aからの距離が0ｍなので，M=FLより，M=0となります。
次に，時計回り・反時計回りの力のモーメントを考えます。
時計回り：M時計回り ＝ 30×4 ＝120 N・m
反時計回り：M反時計回り ＝ 20×6 ＝120 N・m
時計回りの力のモーメント＝反時計回りの力のモーメントということは，力のモーメントがつり合っているということが分かります。
以上のように，力がつり合っているかつ，力のモーメントもつり合っていることから，剛体もつり合っていることが分かり，この剛体はきちんと静止していることが分かります。
例題
例題2
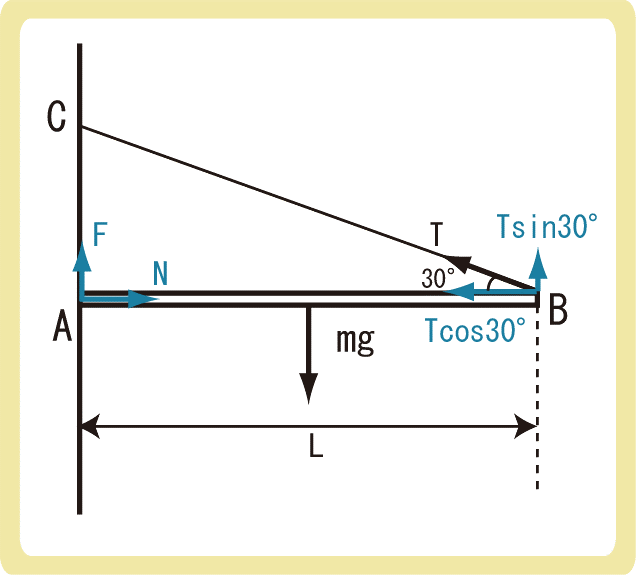
下図のように，長さL，質量mの一様な棒（重心が中央）ABの一端Aを，あらくて鉛直な壁に押しつけた。この棒の他端Bを糸につなぎ，糸を点Cで固定して棒を水平に保つと，棒と糸の間の角度が30°になった。このとき，糸の張力T，棒が壁から受ける静止摩擦力F，棒が壁から受ける垂直抗力Nをそれぞれ求めよ。ただし，重力加速度をgとする。
剛体のつり合いを聞かれる力のモーメントに関する問題では，まずは物理基礎と同様に物体にはたらく全ての力を図示し，鉛直方向・水平方向の力のつり合いの式を作ります。
その後，回転軸を自分で定め（力が多い点が好ましい），力のモーメントの式を作ります。
・鉛直方向のつり合い
・水平方向のつり合い
・力のモーメントのつり合い
この3つの式を連立することで問題を解くことができます。
なお，力のモーメントの式では，腕の長さをかけることと，力を鉛直成分にすることを忘れないように気をつけましょう。
まず，力を上図のように図示します。必ず描きます。
重力は棒の中心から描きましょう。一様な棒なので，重心が中心になります。
張力Tは斜めの方向なのですぐ分解します。力の図示を間違うと全て間違えてしまうので必ず描けるようにしましょう。
垂直抗力Nは壁から垂直に描きます。
もし摩擦がなかったとしたら，この棒は滑り落ちてしまうため，摩擦力は上向きです。
次に力のつり合いを考えます。鉛直方向の力はF，Tsin30°，mgなので
$$F+Tsin30°=mg・・・①$$
水平方向の力はNとTcos30°なので，
$$N=Tcos30°・・・②$$
となります。
最後に，力のモーメントのつり合いを考えます。
この問題では，剛体が静止しているので，回転軸を自分で決めることができます。
FとNのある，力の多い点Aを回転軸としましょう。点Aを回転軸にすることで，点Aからの長さが0のFとNによる力のモーメントを考えなくてもよくなります。
なお，実際に剛体が回転している場合は，実際の回転軸を回転軸としましょう。
モーメントは腕の長さ（回転軸とした点Aからの長さ）×力です。
棒を時計回りに回そうとしている力はmg，反時計回りに回そうとしているのはTsin30°なので
$$\frac{1}{2}L×mg=L×Tsin30°・・・③$$
となります。重力mgは棒の中心にあるので長さがLの半分であることに注意しましょう。
あとは3つの式を連立して解けば終わりです。
③より
$$\frac{1}{2}L×mg=L×T×\frac{1}{2}\\
T=mg$$
このTを①と②にそれぞれ代入します。①より，
$$F+mg×\frac{1}{2}=mg\\
F=\frac{1}{2}mg$$
②より，
$$N=mg×\frac{\sqrt{3}}{2}\\
N=\frac{\sqrt{3}}{2}mg$$
∴\(T=mg \)
\(F=\frac{1}{2}mg \)
\(N=\frac{\sqrt{3}}{2}mg \)
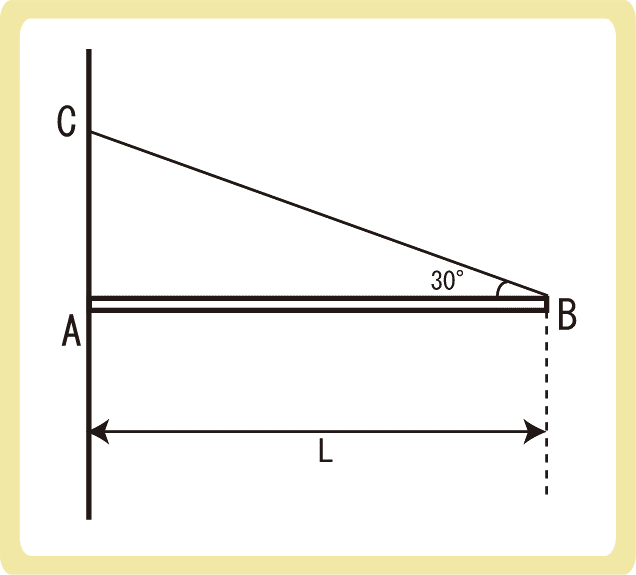
例題3
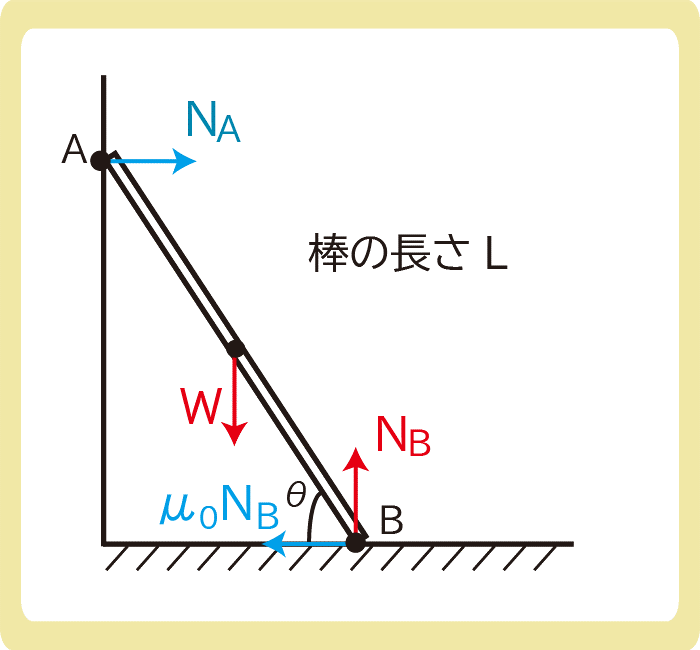
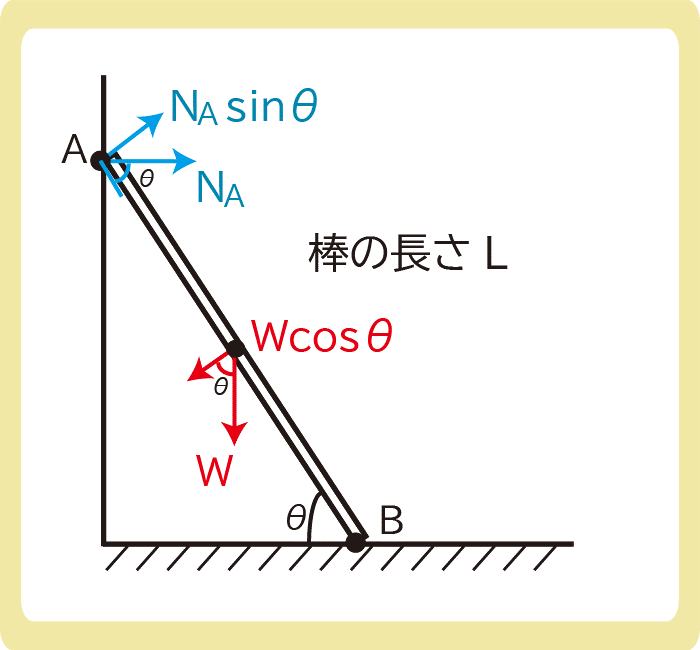
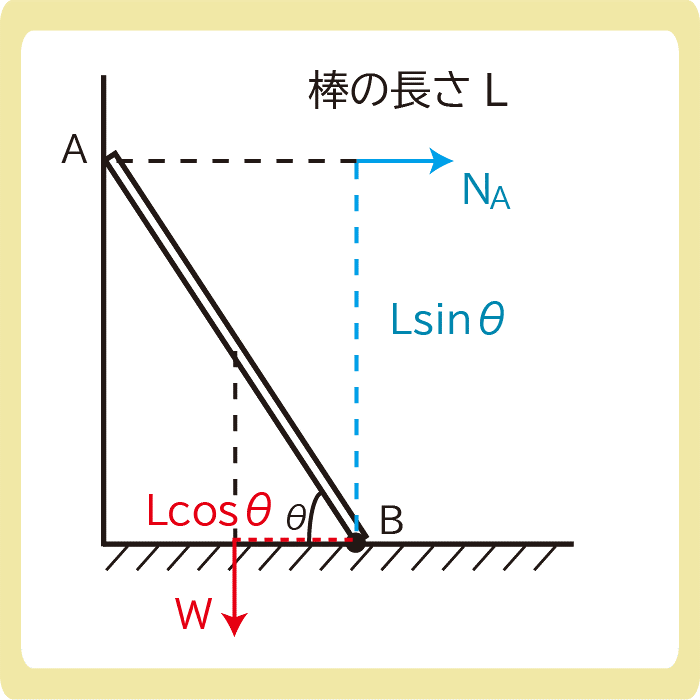
下図のように，長さLの一様な棒を，粗くて水平な床と滑らかで鉛直な壁の間に立てかけた。この棒がちょうどすべり始めるような，棒と床のなす角度θの条件を求めよ。ただし，棒と床との間の摩擦係数をμ0とする。
例題2と同様，まずは物体にはたらく全ての力を図示し，鉛直方向・水平方向の力のつり合いの式を作ります。
その後，回転軸を自分で定め（力が多い点が好ましい），力のモーメントの式を作ります。
垂直抗力はN，重力はWとします。摩擦力はμNです。
力を図示したら，力のつり合いを考えましょう。
$$N_A=μ_0N_B・・・①$$
$$W=N_B・・・②$$
次に，力のモーメントのつり合いを考えます。
回転軸は，力の多いBにしてください。
力が腕に垂直ではない場合，力を分解して，腕に垂直な成分を考えなければいけません。
上図のように，なんとかして力を分解できるようにしましょう。
$$N_Asinθ×L=Wcosθ×\frac{1}{2}L・・・③$$
棒は一様なため，重力のかかる位置は点Bから\(\frac{1}{2}\)Lです。
なお，力を分解せず，力を移動させて考える方法もあります。
力のモーメントでは，力を作用線の方向に動かすことができるため，力をそれぞれ力の向きに移動し，Bからの長さを，ぞれぞれ，LsinθとLcosθにして式を作っても大丈夫です。
自分の分かりやすいと思った方法で問題を解きましょう。
①と②より，
$$N_A=μ_0W$$
となり，これを③に代入すると，
$$N_Asinθ×L=Wcosθ×\frac{1}{2}L\\
μ_0Wsinθ×L= Wcosθ×\frac{1}{2}L \\
μ_0sinθ=\frac{1}{2}cosθ\\
tanθ=\frac{1}{2μ_0}$$
∴\(tanθ=\frac{1}{2μ_0}\)
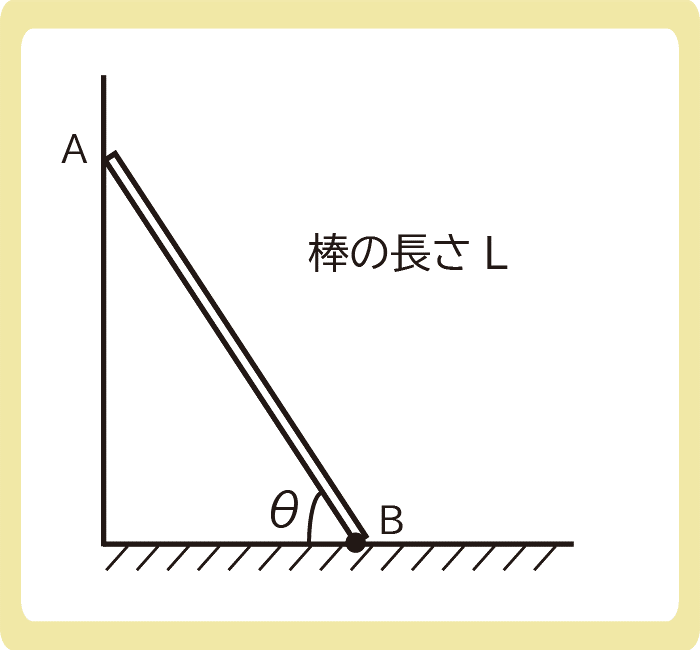
まとめ
物体を引っ張ったとき，単純にまっすぐ進むのではなく回転するかもしれないことを考えます。
質点は大きさも形もない質量のある点であり，剛体は大きさと形のある変形しない質量のある物体です。
物体が回転する作用の量のことを，力のモーメントよび，力×腕の長さで表します。
剛体が静止しているとき，力だけではなく力のモーメントのつり合いも考えます。
剛体のつり合いでは，まず力を図示し，力のつり合いの式と力のモーメントを立式します。
力のモーメントのつり合いを考えるときは，力の多い点を回転軸にしましょう。
