・重心とは
・重心の公式
重心という言葉は日常でよく使いますし、数学でも勉強するので、どこかで聞いたことありますよね。
物体の形が一様ではないとき、重心が中心にあるとは限りません。人間の場合、大人ならへその少し下あたりに重心があります。
今回は、重心についてわかりやすく簡単に解説していきます。
重心とは
全質量が集中している点
\(x_G=\frac{m_1x_1+m_2x_2＋…}{m_1+m_2＋…}\)
\(y_G=\frac{m_1y_1+m_2y_2＋…}{m_1+m_2＋…}\)
重心とは全質量が集中している点のことです。
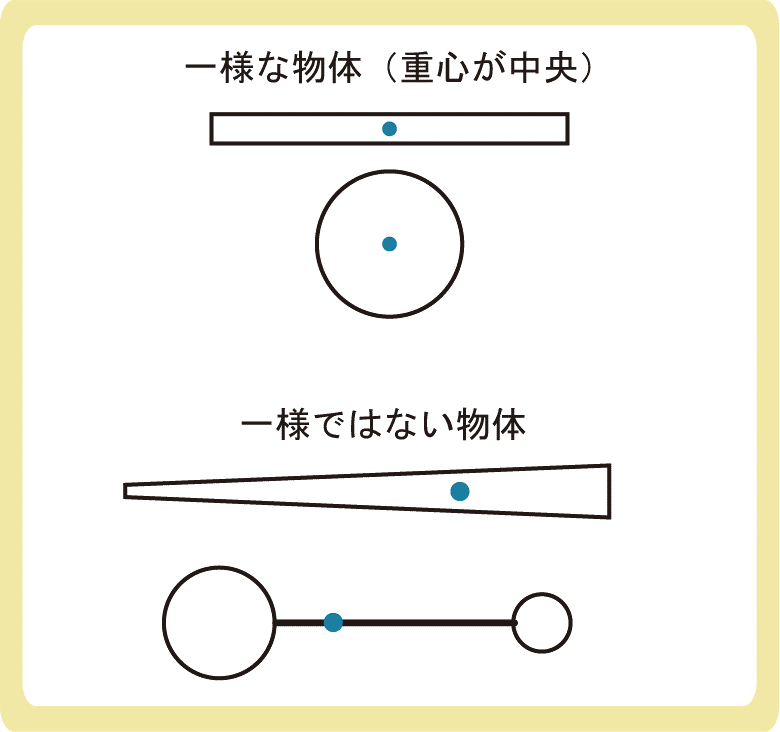
一様な棒や円・長方形等では重心は中央にありますが、シャーペンや傘等の形が一様でない物は重心の位置が中央ではありません。シャーペンを真ん中あたりで支えようとしても回転して落ちてしまいますよね。
しかし、シャーペンを1点で支えることのできる場所がどこかにあります。そのような、質量の中心となる点が重心となります。
重心で支えるとき物体は回転しません。つまり、重心を回転軸とするとモーメントがつり合っています。これを利用して公式を導きましょう。
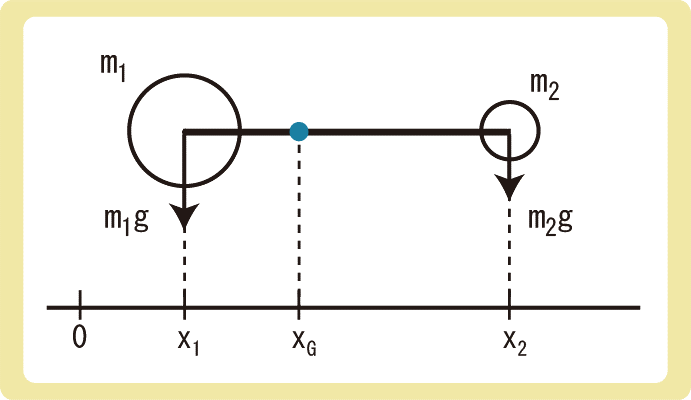
上図のように、質量がm1、m2である2つの一様な球が、軽い(質量の無視できる)棒で繋がっているとします。
左側の球の重心の位置をx1、右側の球の重心の位置をx2、2つの共通重心の位置をxGとするとき、xGをm1、m2、x1、x2で表してみましょう。
重心で支えるとき物体は回転しないので、重心を回転軸とし、力のモーメントのつり合いを考えます。
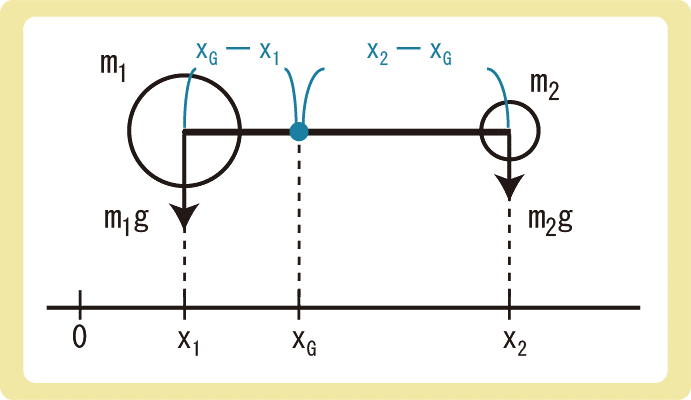
力のモーメントは力×腕の長さなので、
$$m_1g×(x_G-x_1)= m_2g×(x_2-x_G)\\
m_1x_G-m_1x_1=m_2x_2-m_2x_G\\
m_1x_G+m_2x_G=m_1x_1+m_2x_2\\
x_G(m_1+m_2)=m_1x_1+m_2x_2\\
x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}$$
となり、これが重心の公式となります。
物体が3つ以上の場合でも同様な結果となることと、y座標で考えても同じなため、まとめて
$$x_G=\frac{m_1x_1+m_2x_2＋…}{m_1+m_2＋…}$$
$$y_G=\frac{m_1y_1+m_2y_2＋…}{m_1+m_2＋…}$$
と表します。
例題
例題1
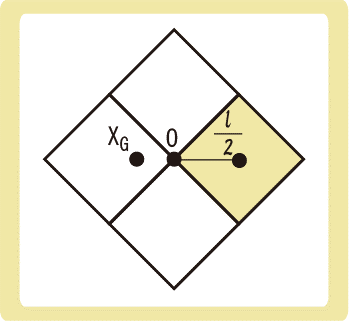
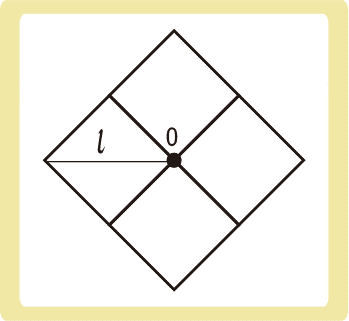
下図のように対角線の長さが\(l\)の質量mの一様な正方形が4つある。一番右にある正方形を取り除いたとき、残りの3つの正方形からなる物体の重心の位置はどこか。
重心を求める問題では、公式を使って解くことが多いので、必ず公式を覚えておきましょう。
点Oを中心とすると、元々あった4つの物体の重心の位置は点O、取り除いた正方形の重心の位置は点Oから右に\(\frac{l}{2}\)となります。また、残り3つの正方形からなる物体の重心の位置をxGとします。
重心の位置は4つの正方形から1つの正方形を失った場所にあるので、点Oを基準とすると、
\(x_G=\frac{m_1x_1+m_2x_2＋…}{m_1+m_2＋…}\)より
元の4つの正方形の質量は4ｍで、点Oからの距離が0
正方形を1つ取ったので、質量がーｍ、点Oからの距離が\(\frac{l}{2}\)であることを代入します。
$$x_G=\frac{4m×0-m×\frac{l}{2}}{4m-m}\\
x_G=-\frac{l}{6}$$
∴点Oから左方向に\(\frac{l}{6}\)の位置
まとめ
重心とは、全質量が集中している点のことです。
重心で物体を支えると、物体は回転しないため、\(x_G=\frac{m_1x_1+m_2x_2＋…}{m_1+m_2＋…}\)という公式を導くことができます。
重心の問題が出題することはそこまで多くないのですが、重心の問題では公式を使うことが多いため、上の式だけはちょくちょく復習しておくと良いです。
