・運動量とは
・力積とは
・運動量と力積の関係
運動量と力積、運動量保存則、反発係数の範囲ではボウリングのピンを倒したとき、車と車が衝突したときのような、「物体と物体が衝突したあと、どう運動するのか」について考えます。
今回は、その基礎でもある運動量と力積について、わかりやすく簡単に解説していきます。
運動量とは
質量と速度の積
物体の勢いを表す
$$\vec{p}=m\vec{v}$$
運動量とは、質量と速度の積のことです。記号はp、単位は[kg・m/s]です。
イメージとしては、物体の勢いのようなものであり、式は\(\vec{p}=m\vec{v}\)と表します。
pという記号はあまり使わないので、 原子の分野に入るまで忘れていても大丈夫です。
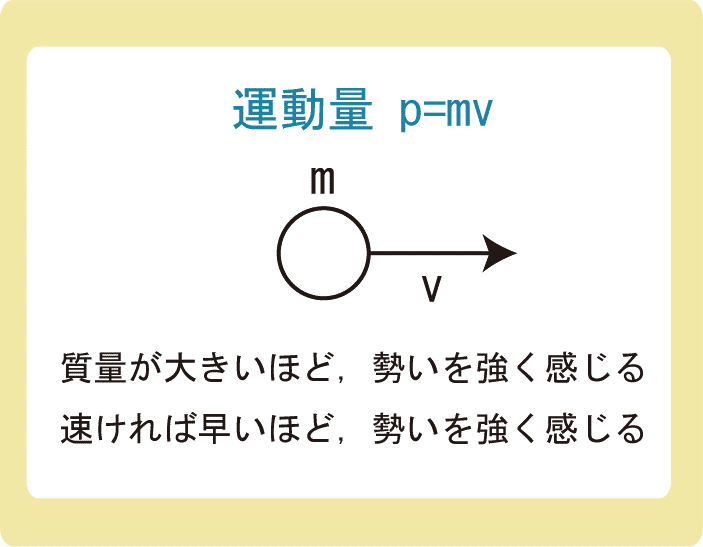
同じ速さでも、車とトラックだとトラックの方が”勢い”を強く感じます。
同じ車でも、速ければ速いほど、”勢い”を強く感じます。
このような量のことを、運動量と定義しましょう。
力積
力と時間の積のこと
$$\vec{I}=\vec{F}Δt$$
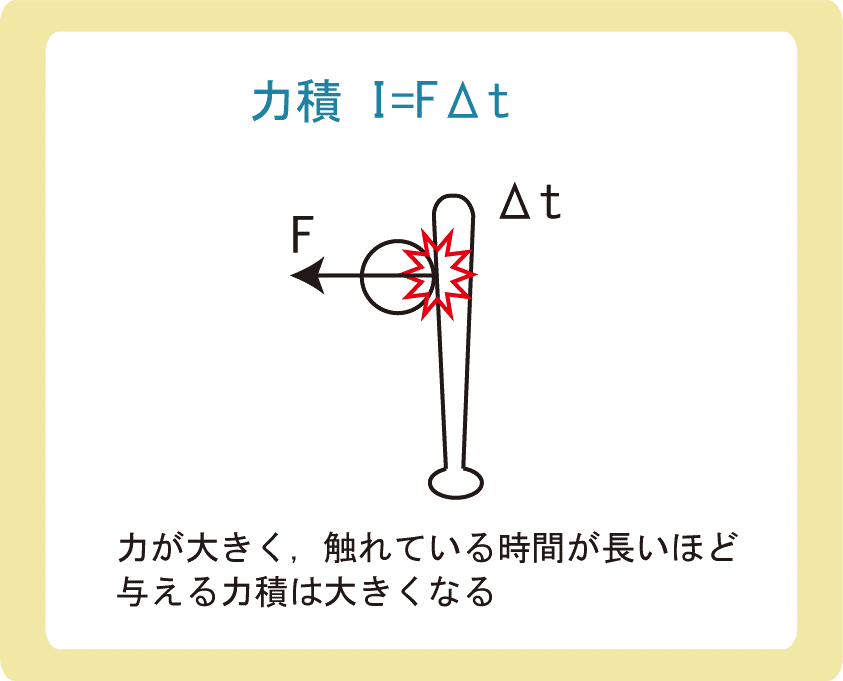
力積とは、力と時間の積のことです。記号はI[N・s]を使うのですが、Iという記号を使う機会はほぼありません。
式は\(\vec{I}=\vec{F}Δt\)であり、同じ大きさの力であっても、力のはたらいている時間が長いほど、力積も大きくなります。
運動量と力積の関係
$$m\vec{v’}- m\vec{v}= \vec{F}Δt$$
運動量と力積には、\(m\vec{v’}- m\vec{v}= \vec{F}Δt\)という関係式が成り立ちます。
運動量の単位は[kg・m/s]であり、力積の単位は[N・s]です。
単位の説明でも話しましたが、[N]=[kg・m/s2]であるため、力積の[N・s]は[kg・m/s]となり、運動量の単位と一致します。
不思議な感覚かもしれませんが、質量と速度を掛けたものと、力と時間を掛けたものは単位が同じになるのです。
例題
例題1
東向きに速さ20m/sで進んでいる質量0.20kgのボールがある。以下の問に答えなさい。
(1)このボールの運動量の大きさは何kg・m/sか。
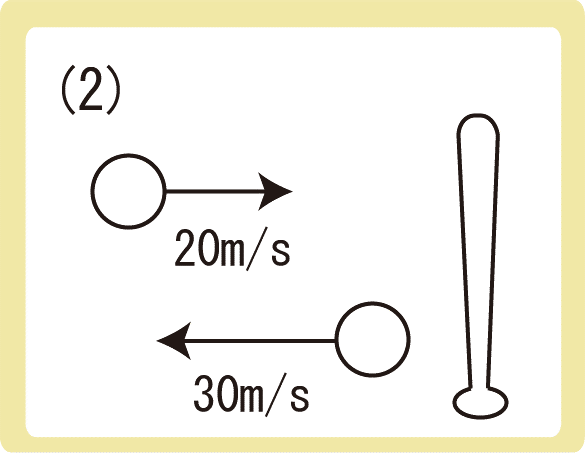
(2)ボールをバットで打ち返したところ、ボールの速度は西向きに30m/sとなった。ボールの受けた力積はどちら向きに何N・sか。
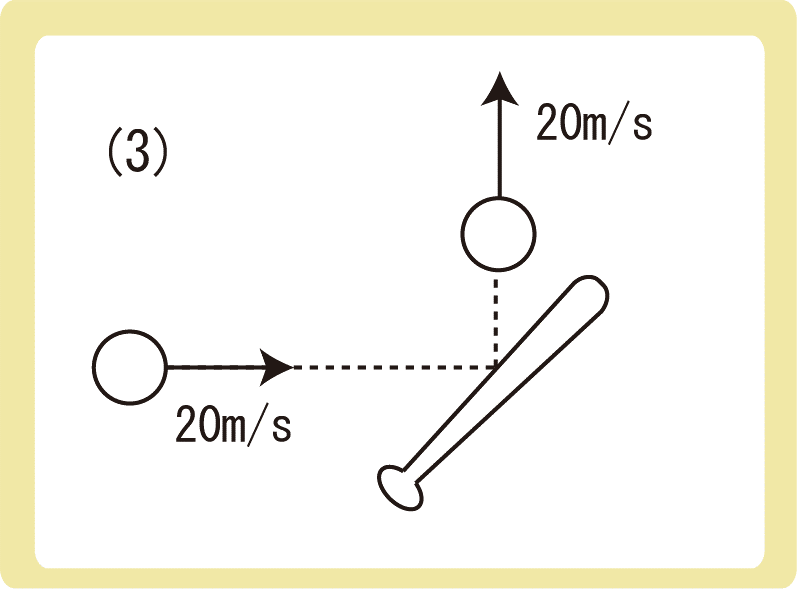
(3) ボールをバットで打ち返したところ、ボールの速度は北向きに20m/sとなった。ボールの受けた力積はどちら向きに何N・sか。
まとめ
運動量は質量と速度の積のことであり、力積は力と時間の積のことです。
運動量はmv、力積はFΔtと覚えておきましょう。
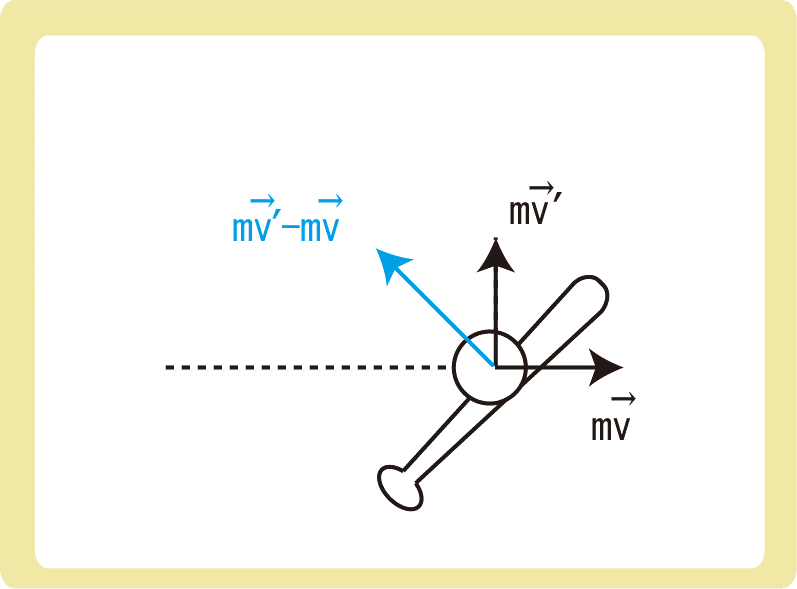
運動量と力積には\(m\vec{v’}- m\vec{v}= \vec{F}Δt\)という関係式があります。ベクトルの引き算であるため、相対速度と同様に、図を用いてベクトルの引き算を行いましょう。