運動量保存の法則とは

運動量保存の法則は，物理の中でも重要な保存則の1つです。
保存則といえば，エネルギー保存の法則を思い浮かべる人が多いと思います。エネルギー保存の法則はエネルギーが変わらない法則であり，運動量保存の法則は運動量が変わらないという法則です。
運動量が変わらないことによって，どのような運動について理解することができるのでしょうか。

今回は，運動量保存の法則について，わかりやすく簡単に解説していきます。

運動量保存の法則とは

運動量保存の法則とは，内力のみを受けるとき，運動量の総和は変化しないという法則のことです。

物体と物体が衝突するときを考えます。
普通，物体が衝突すると内部摩擦で熱が発生したり変形したりするので，力学的エネルギーは保存されません。外部から力が加えられないとき，物体と物体が衝突しても運動量は保存されます，これを運動量保存の法則といいます。

運動量保存の法則の導出

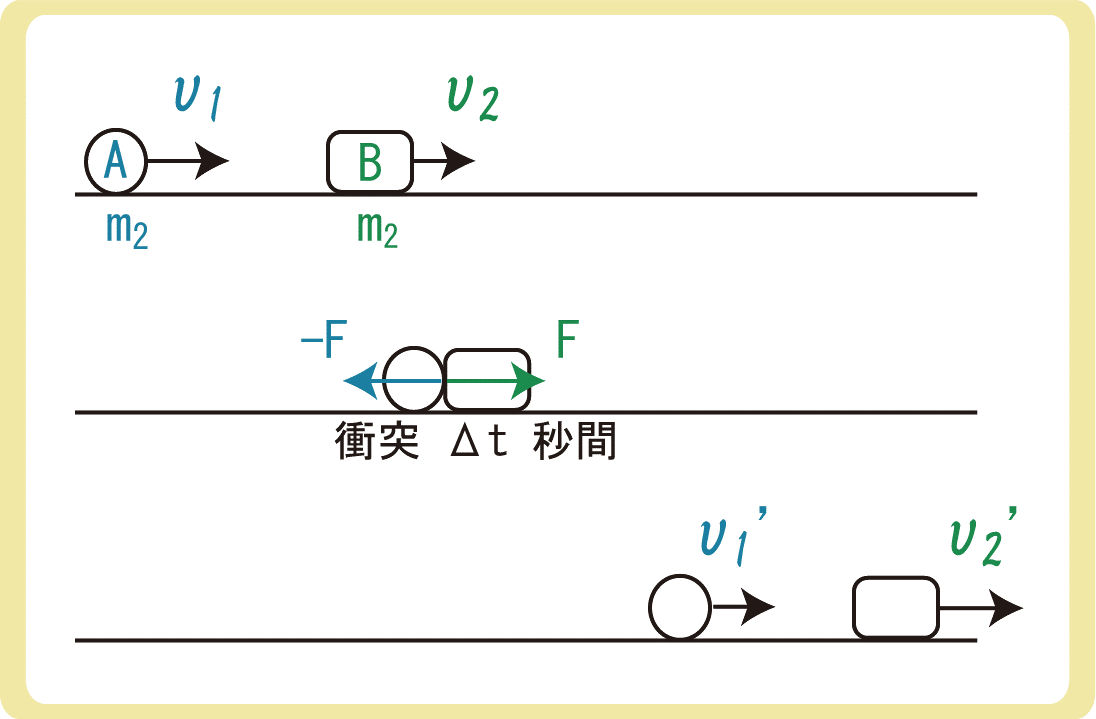
上図のように，右向きに速さv₁で運動している質量m₁の物体Aと，右向きに速さv₂で運動している質量ｍ₂の物体Bの2つの物体の衝突について考えます。
AとBがΔｔ秒の間衝突したときに発生した力の平均の大きさをFとし，物体Aの速さは右向きにv₁’，物体Aの速さは右向きにv₂’になったとします。

運動量と力積の関係より

$$m_1v_1’-m_1v_1=-FΔt・・・①$$

$$m_2v_2’-m_2v_2=FΔt・・・②$$

と，式を作ることができます。
補足ですが，作用反作用の法則より，2つの物体にはたらく力の大きさは等しく，物体Aにはたらく力は左向きなので，-Fとしています。

①，②より

$$\frac{m_1v_1’-m_1v_1}{m_2v_2’-m_2v_2}=\frac{ -FΔt }{ FΔt }\\
\frac{m_1v_1’-m_1v_1}{m_2v_2’-m_2v_2}=-1\\
m_1v_1’-m_1v_1=-m_2v_2’+m_2v_2\\
m_1v_1+m_2v_2= m_1v_1’+m_2v_2’$$

となり，運動量保存則の法則の公式を導出することができます。

例題

例題1

下図のように，速さ4.0m/sで運動している質量2.0kgの小球Aが，静止している質量5.0kgの物体Bに衝突したところ，小球Aの速さは逆向きに1.0m/sとなった。衝突後の物体Bの速さは何m/sか。

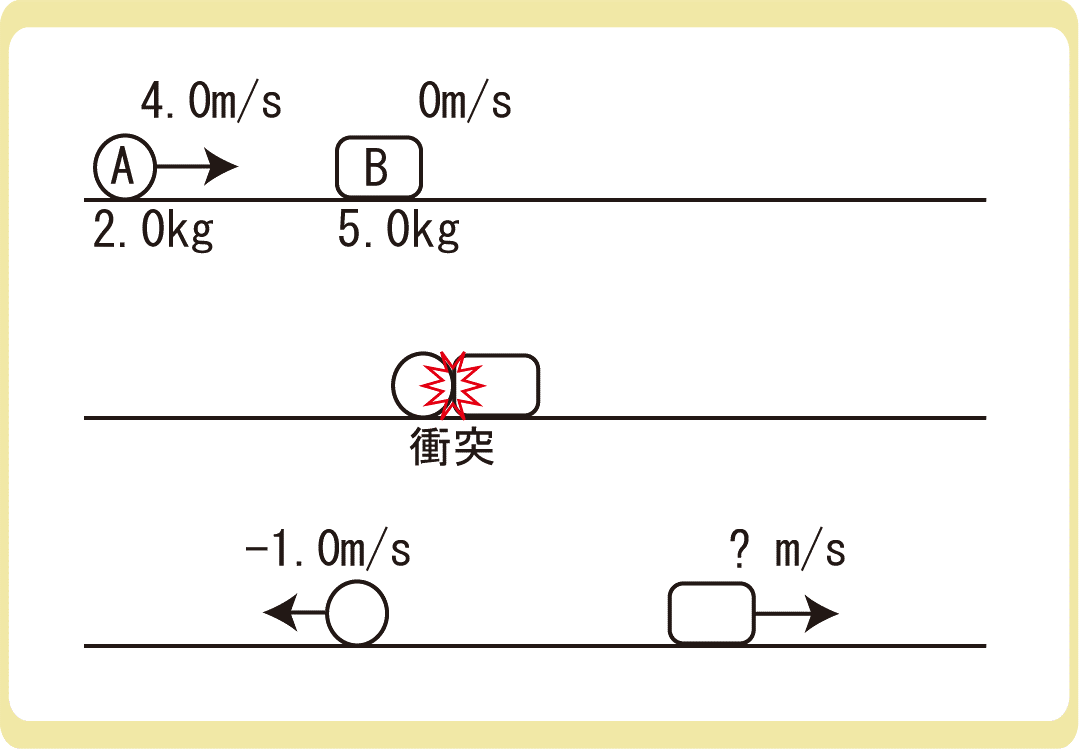
例題2

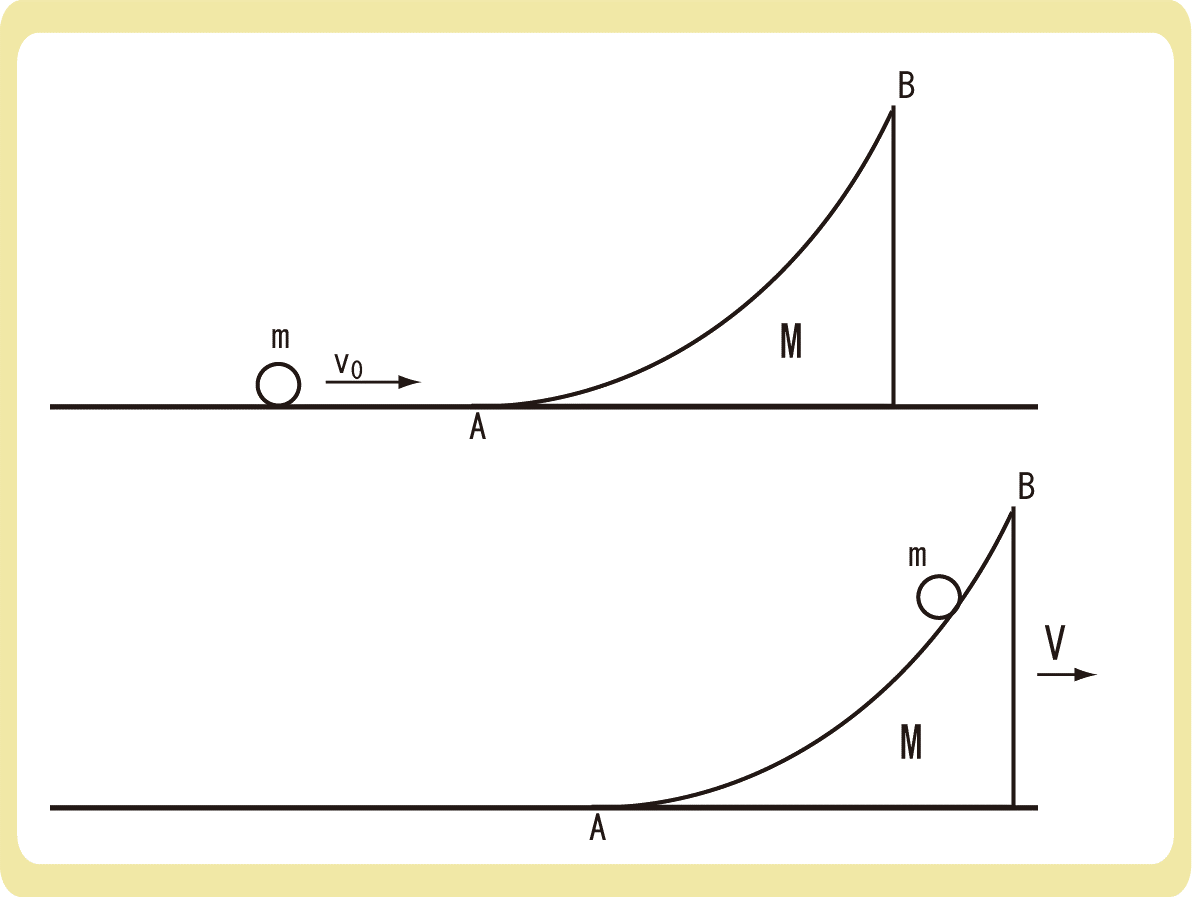
下図のように，なめらかな水平面上に，なめらかな曲面ABをもつ質量Mの台が置かれている。質量mの小球がv₀の速さで曲面ABを登り始めた。小球が最高点に達したとき，台の速度Vを求めなさい。ただし，水平面と曲面ABはなめらかに接続されているものとし，小球は曲面ABを超えることがないとする。

例題3

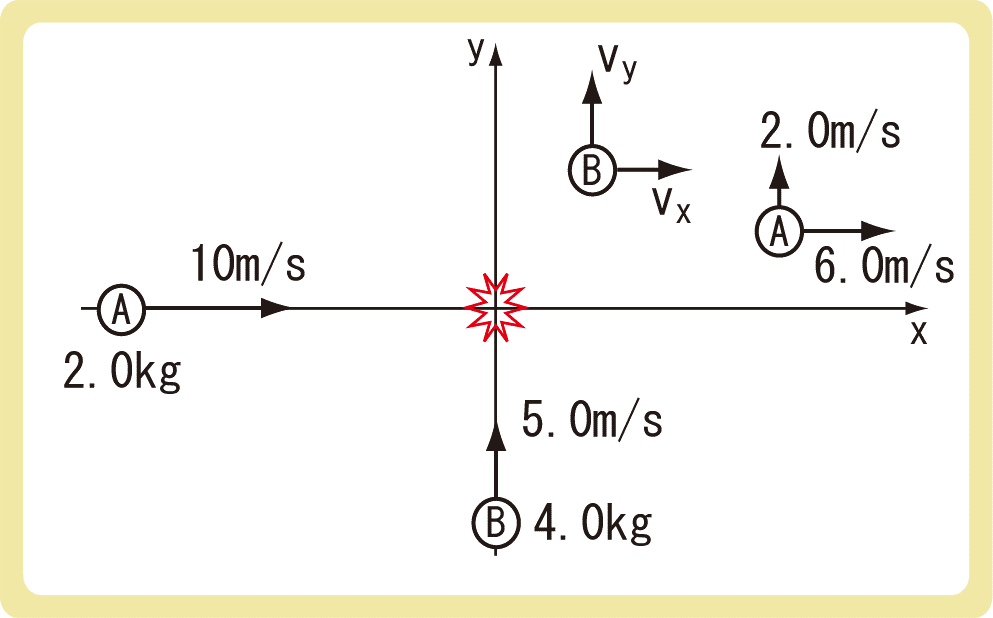
x軸正の向きに10m/sで進んでいる質量2.0kgの小球Aと，y軸正の向きに5.0m/sで進んでいる4.0kgの小球Bが衝突したところ，小球Aの速度のx成分が6.0m/s，y成分が2.0m/sとなった。小球Bの速度のx成分v_xとy成分v_yを求めよ。

まとめ

内力しかはたらかない場合，その系では運動量保存の法則が成り立ちます。
内力のみはたらく例として物体と物体の衝突がよく登場しますが，分裂，合体，上の例題2のような問題，摩擦のある物体の上を物体が動いている問題など，パターンは様々なので，色々な問題を解くことをオススメします。

 

次の内容はこちら

一覧に戻る