・反発係数とは
・反発係数と高さの関係
粘土を落としても跳ね返らないですが、スーパーボールはよく跳ね返ります。
同じボールであっても、絨毯の上に落とすよりも体育館の床に落とした方がよく跳ね返ります。
今回は、物体と床(物体)が衝突したときの跳ね返りやすさ(反発係数)について、わかりやすく簡単に解説していきます。
反発係数とは (はね返り係数とは)
衝突前後の相対速度の比
物体の跳ね返りやすさを表す
$$0≦e≦1$$
e=1 弾性衝突
$$e=-\frac{v_A’-v_B’}{v_A-v_B}$$
反発係数とは、衝突前後の相対速度の比のことをいいます。
簡単にいうと「物体の跳ね返りやすさ」のことであり、記号はe (単位なし)、その値は\(0≦e≦1\)です。
大雑把に、粘土は床に叩きつけても跳ね返らないので反発係数が小さく、スーパーボールは跳ね返りやすいので反発係数が大きい、というイメージで大丈夫です。
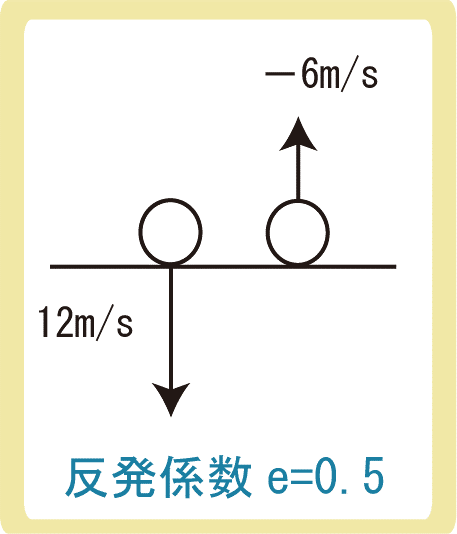
反発係数の求め方は単純で、衝突前後の相対速度の比を考えます。
例えば、12m/sの速さで床に衝突した物体が6m/sで跳ね返ったとします。速さの比を考えると\(\left|\frac{-6}{12}\right|=0.5\)となり(跳ね返っているので速度が逆向きになり、マイナスが付いている)、速さが半分になったことが分かります。従って、この場合の反発係数e=0.5です。
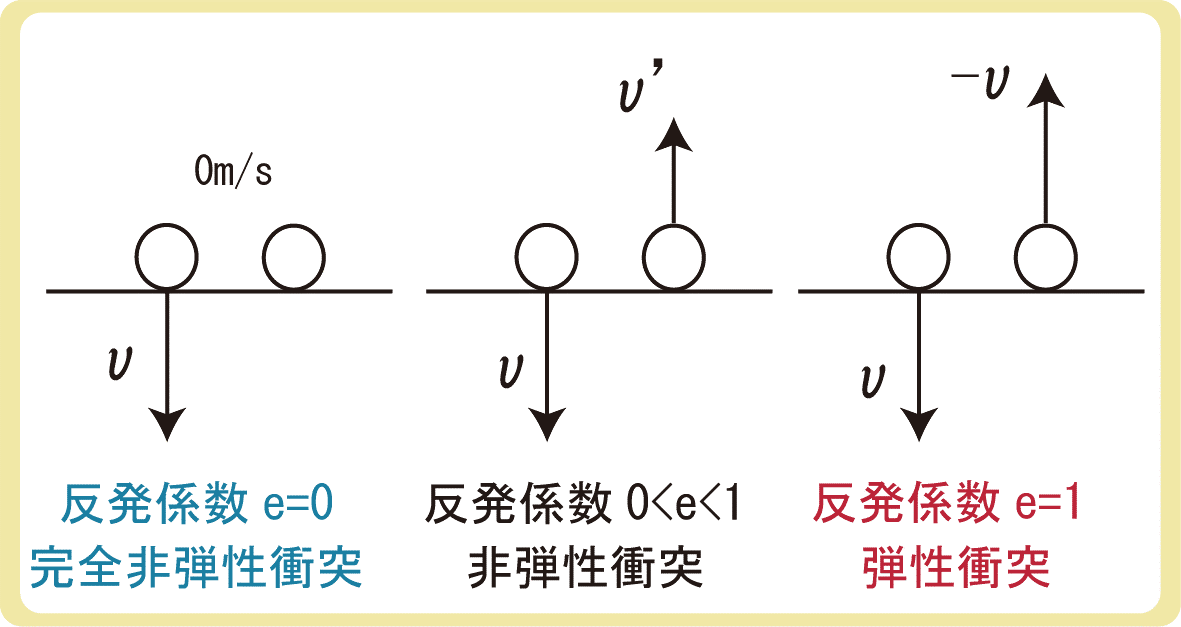
また、反発係数e=0のことを完全非弾性衝突、反発係数0<e<1のことを非弾性衝突、反発係数e=1のことを弾性衝突といいます。弾性衝突と書いてあるときは、反発係数e=1であると察する必要があります。弾性衝突という名前はたまに登場するので、ここで覚えておきましょう。
なお、反発係数は0≦e≦1です。
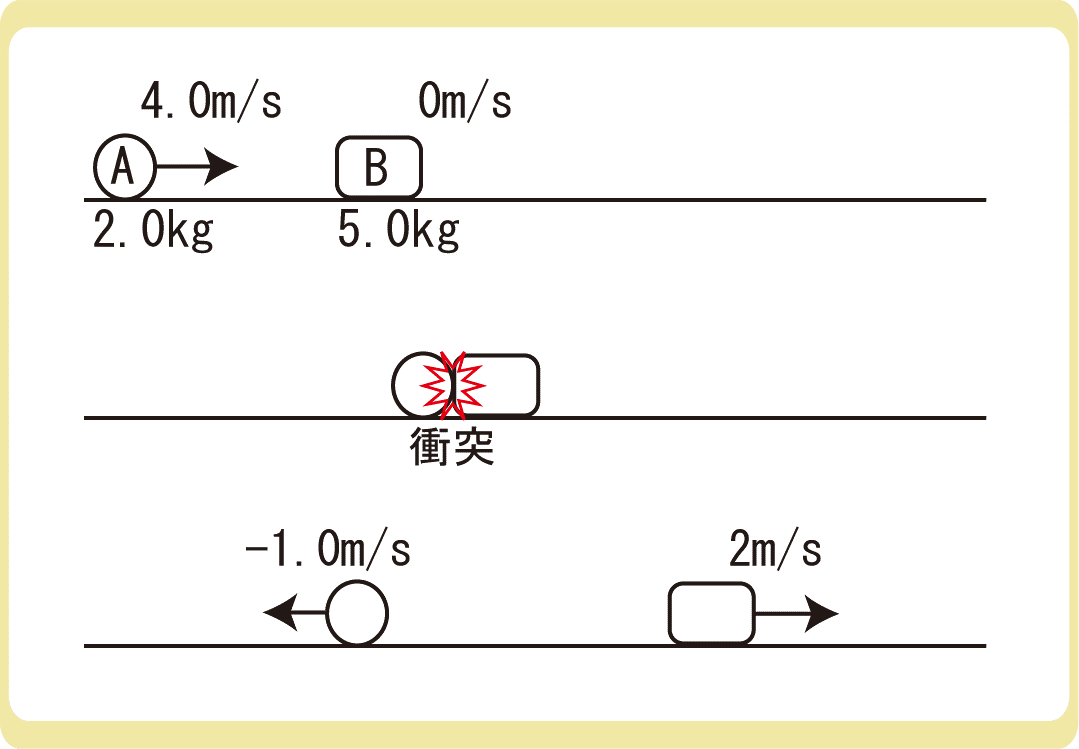
反発係数とは衝突前後の相対速度の比のことであり、単純な速度の比ではありません。上では、相対速度を簡単に考えるため「物体と床」の衝突を考えましたが、一直線上にある2つの物体の衝突について考えてみましょう。
上図のように、4m/sで動いていた小球Aが、小球Bに衝突することにより速度が－1m/sになりました。先ほどのように速度の比を考えると、反発係数は\(e=\left|\frac{-1}{4}\right|=0.25\)となるように思えるのですが、小球Bも動いているのでBから見たAの速度が変わります。
Bから見たAの相対速度は－3m/sであるため、反発係数は\(e=\left|\frac{-3}{4}\right|=0.75\) となります。
つまり、反発係数の公式は相対速度を用いて\(e=-\frac{v_A’-v_B’}{v_A-v_B}\)と表すことができます。
相対速度を考えると分子は必ずマイナスになるので、公式にもマイナスを付けています。よく忘れてしまうので注意しましょう。
反発係数と高さの関係
$$h’=e^2h$$
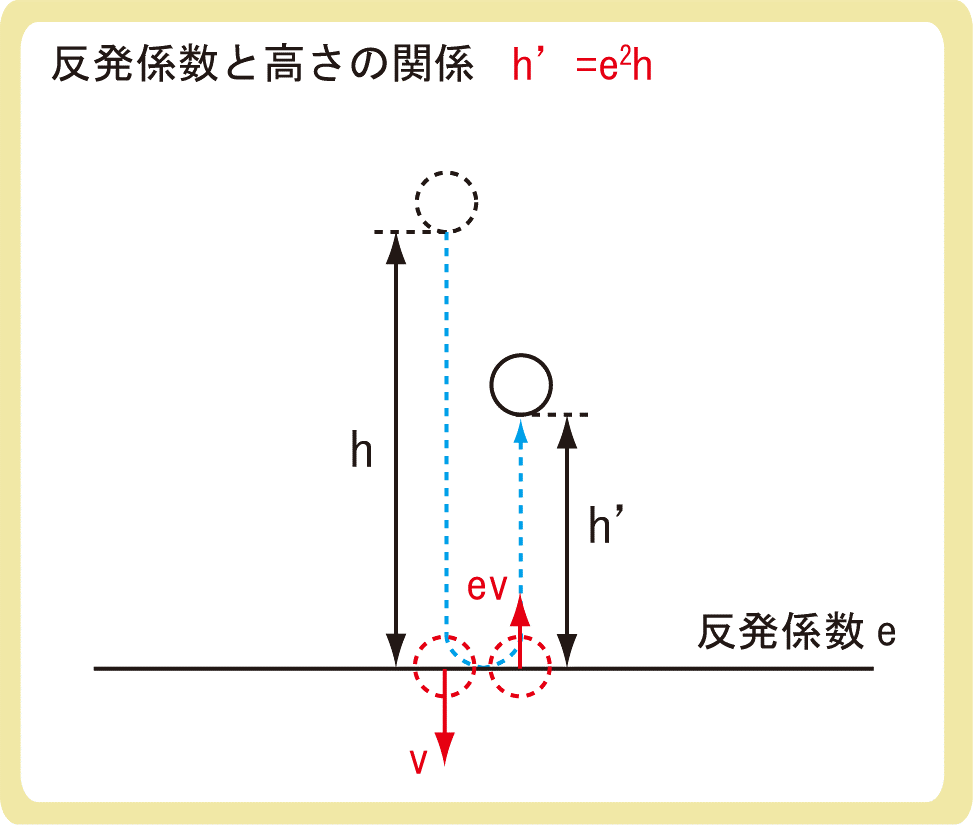
上図のように、高さhにある物体を自由落下させところ、水平面に衝突し、高さh’まで跳ね返ったとします。
このとき、水平面に衝突する直前の物体の速度vは、エネルギー保存の法則より、
$$\frac{1}{2}mv^2=mgh\\
v=\sqrt{2gh}$$
となり、反発係数をeとすると、跳ね返った直後の速さは
$$ev=e\sqrt{2gh}$$
となります。エネルギー保存の法則をもう一度使い、跳ね返った後の最高点の高さh’を求めると
$$\frac{1}{2}m×(ev)^2=mgh’\\
\frac{1}{2}×m×e^2×(\sqrt{2gh})^2=mgh’\\
e^2h=h’$$
となります。
反発係数が0.5であれば、物体を落として跳ね返った後の最高点の高さは、e2=0.25なので0.25倍の高さ、e=0.9であればe2=0.81倍の高さになるということです。
\(h’=e^2h\)という式を知らなくても問題を解くことはできるのですが、知っていると簡単に問題を解くことのできる場合があるので、ぜひ覚えておきましょう。
例題
例題1
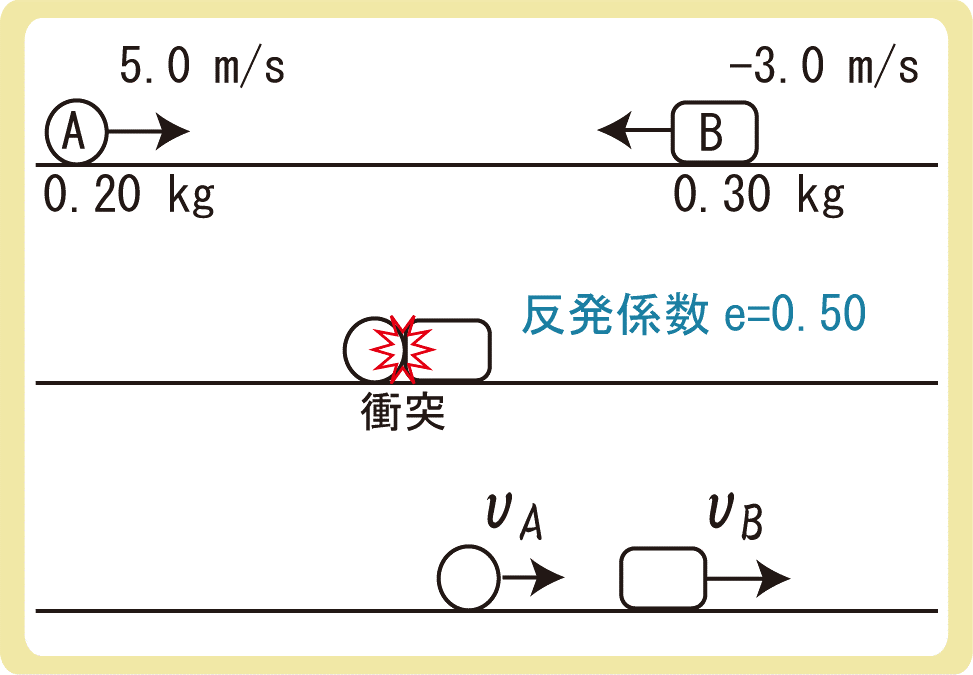
速さ5.0m/sで進んでいる質量0.20kgの小球Aと、速さ3.0m/sで進んでいる質量0.30kgの小球Bが正面衝突した。2つの小球間の反発係数が0.50のとき、衝突後の2つの小球の速度をそれぞれ求めよ。ただし、小球Aが初めに進んでいた方向を正とする。
ますは図を描きましょう。
衝突後のAとBの速度をvA、vBとします。vAとvBの向きは分からないので、とりあえず正の向きとして図示しておきましょう。
今回求めるのは小球AとBの速度の2つなので、使う式も2つ用意する必要があります。
運動量保存の法則と反発係数、2つの式を使うことで求めましょう。
運動量保存の法則より
0.1=0.2v_A+0.3v_B\\
1=2v_A+3v_B・・・①$$
反発係数が0.50であるため
$$0.5=-\frac{v_A-v_B}{5.0-(-3.0)}\\
4=-v_A+v_B・・・②$$
あとは、①と②を連立すればよいので、①・②より、
\(v_A=-2.2, v_B=1.8\)
∴Aの速度：負の向きに2.2 m/s, Bの速度：正の向きに1.8 m/s
Aの速度を正の向きとして図示しましたが、計算した結果、負の向きであると教えてくれるため、AちBの速度の向きが分からない場合は、とりあえず正の向きとして図示しておいて大丈夫です。
例題2
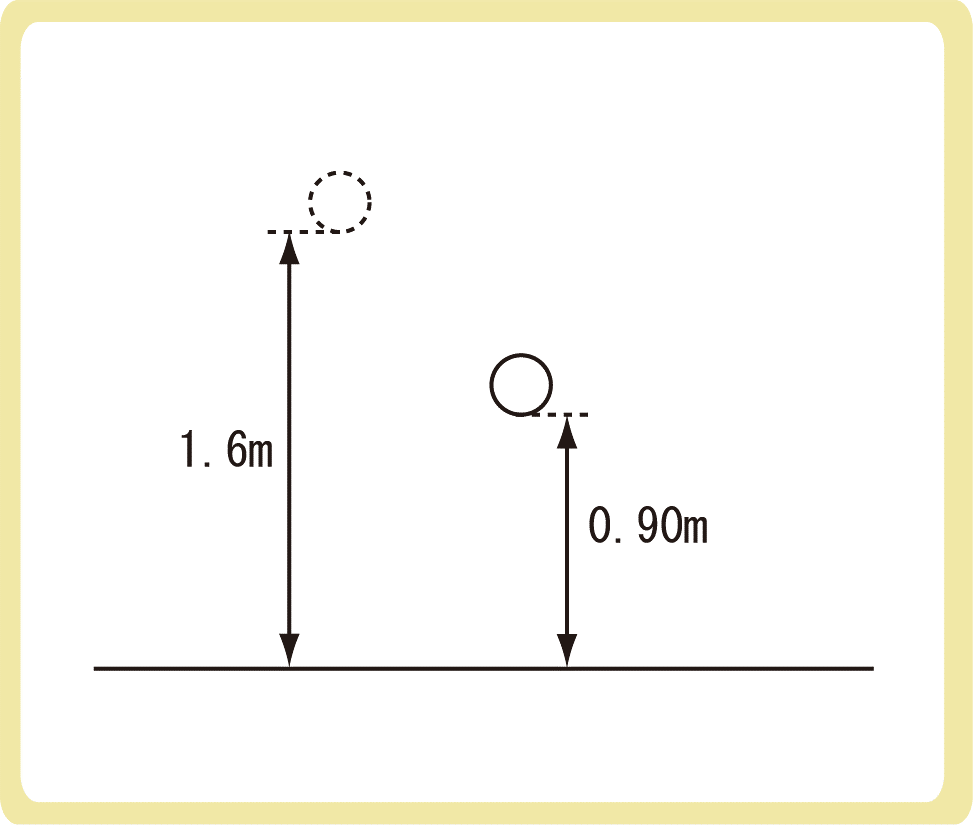
1.6mの高さから小球を静かに落としたところ、水平面に衝突し、0.90mの高さまで跳ね返った。以下の各問に答えなさい。
(1)小球と水平面との間の反発係数を求めなさい。
(2)0.90mの高さまで跳ね返った小球が再び水平面に衝突し跳ね返った。このとき、再び跳ね返った小球の最高点の高さを求めなさい。
まとめ
反発係数とは、衝突前後の相対速度の比のことであり、物体の跳ね返りやすさを表します。
記号はeであり、単位はなく、相対速度の比であることを式にすると
$$e=-\frac{v_A’-v_B’}{v_A-v_B}$$
となります。運動量保存の法則と一緒に登場することが多いですね。
また、物体を自由落下させたときの反発係数と高さには
$$h’=e^2h$$
という関係があり、覚えておくと問題を楽に解ける場合があります。
