・円運動とは
・角速度とは
・円運動の周期
地球を中心に公転する月や、遊園地にあるメリーゴーランドのように、物体が円形の軌道を描く運動を円運動といいます。
万有引力、単振動、波動、電磁気の交流等、円運動は様々な現象と関係のある大切な範囲です。
なお、運動方程式・力学的エネルギー保存の法則を理解していないと解けない問題もあるため、問題の解き方が分からない場合は物理基礎の復習も行いましょう。
今回は、円運動についてわかりやすく簡単に解説していきます。
円運動とは
物体が円形の軌道を描く運動のこと
円運動の中でも一定の速さで回っている運動のことを等速円運動という
円運動とは、物体が円形の軌道を描く運動のことです。
円運動の中でも一定の速さで回っている運動のことを等速円運動といい、地球の周りを月が公転しているような運動を等速円運動として考えます。
ジェットコースターが鉛直方向に一周するような場合は、等速円運動ではなく単なる円運動です。
まずは、円運動に登場してくる様々な文字や定義を紹介します。円運動を勉強している最中に、公式に出てくる文字が分からなくなってしまった場合はここに戻ってきてください。
角速度とは
1秒間に何ラジアン回転するか
ωはギリシャ文字でオメガと読む
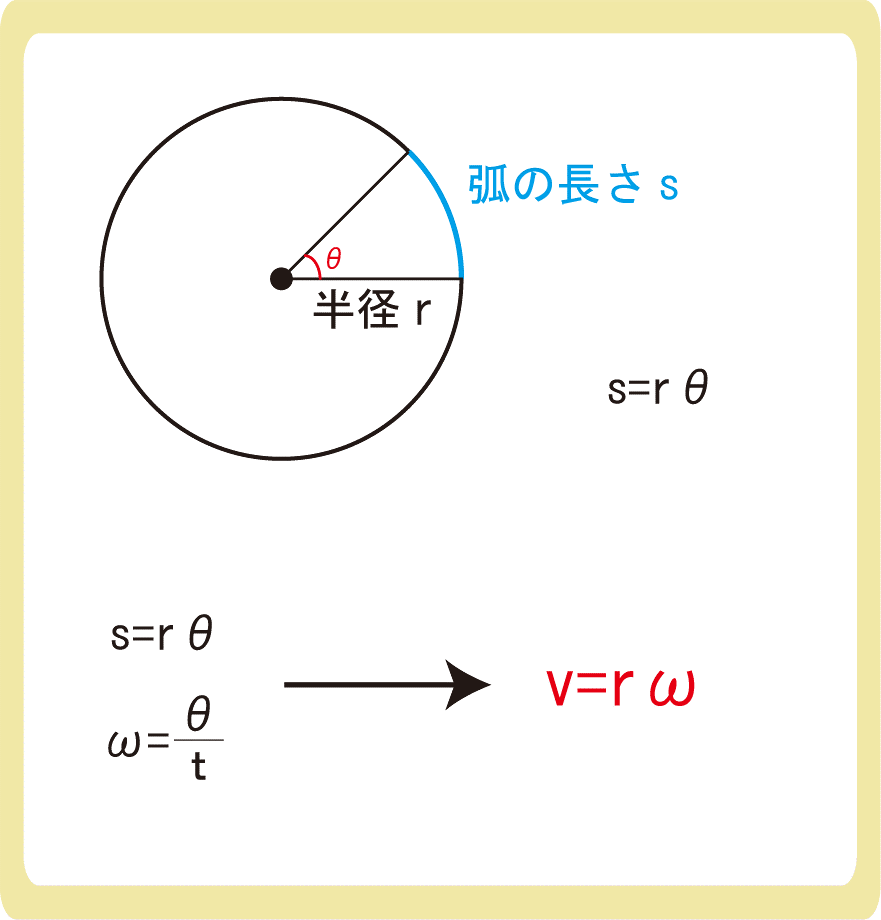
$$ω=\frac{θ}{t}$$
角速度とは、1秒間に何ラジアン回転するかを表した角度に関する速度のことで、記号ω(オメガ)を用いて表します。単位は[rad/s]です。
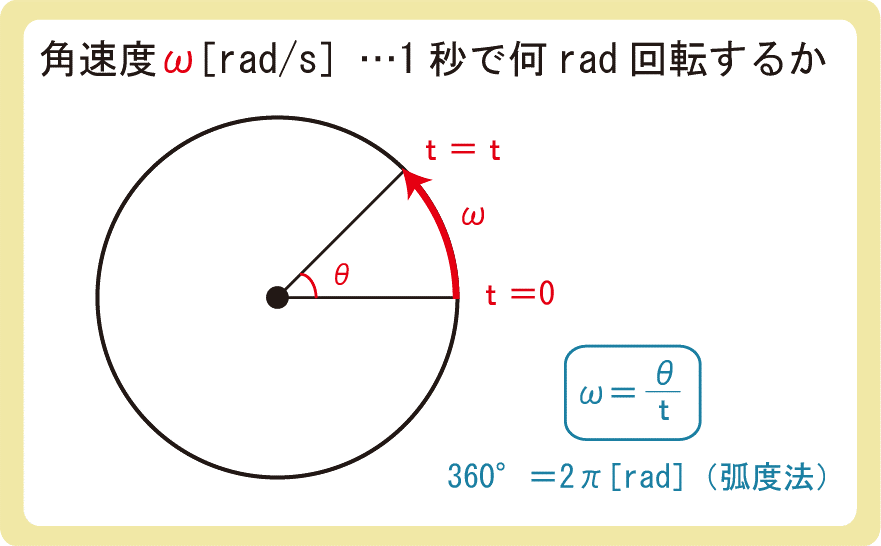
ラジアンとは弧度法における角度の単位のことです。
円運動では角度を[°]ではなく[rad]を用いて考えます。
例えば360°の場合は2π[rad]ですね。
単純に1秒間に何°回転するのかというイメージを持っても良いでしょう。角度の速度なので角速度です。
θ回転するのにかかる時間をtとすると、長さ÷時間で角速度\(ω=\frac{θ}{t}\)となります。この公式は円運動の分野で使うことはありませんが、波動や交流では\(θ=ωt\)として使うことになります。
角速度と速度の公式
$$v=rω$$
速度を\(v\)、半径を\(r\)とするとき、\(v=rω\)という関係が成り立ちます。
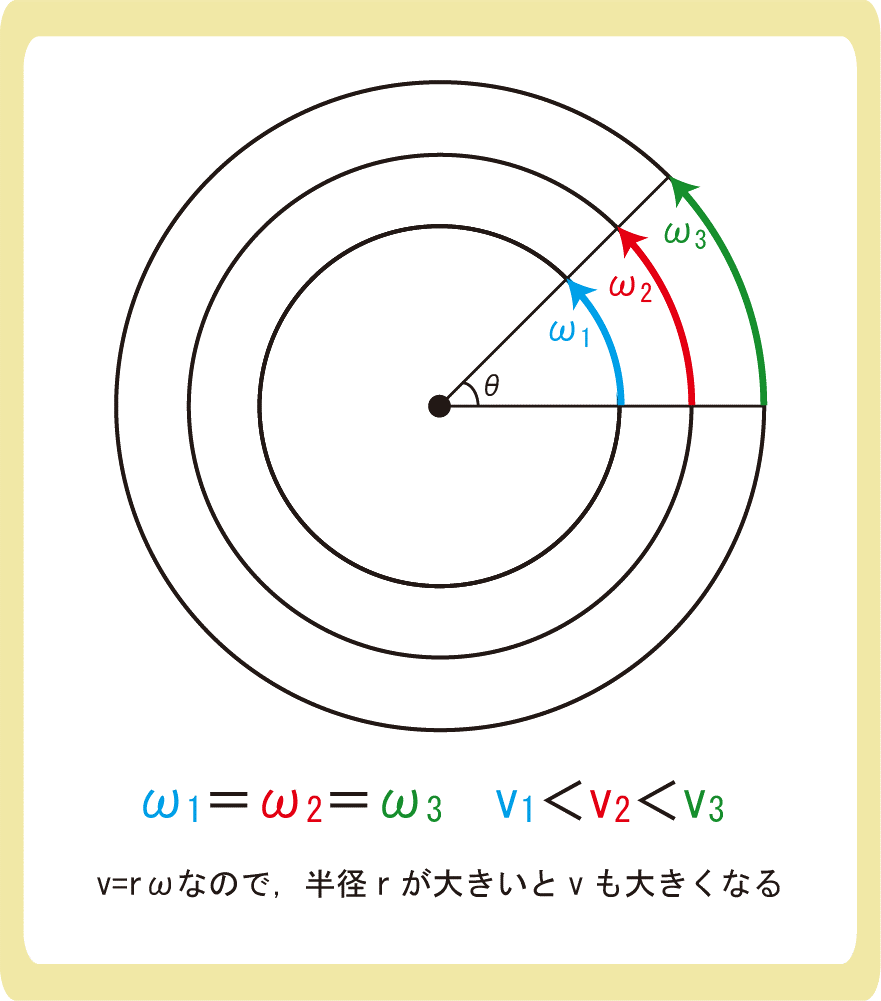
\(v=rω\)に対して、上図のようなイメージを持つと良いでしょう。
3つの円の大きさは異なりますが、角速度は「1秒で回転する角度」であるため、同じ時間で同じ角度だけ回転したのであれば、\(ω_1=ω_2=ω_3\)となります。
しかし、1秒で回転した角度は同じでも、半径が長いと大きく移動する必要があるため、ωが等しくても\(r\)が大きくなると\(v\)も大きくなり、\(v=rω\)と考えることができます。
等速円運動と周期
1回転するのにかかる時間
$$n=\frac{1}{T}$$
(n:回転数[Hz])
$$T=\frac{2πr}{v}\\
T=\frac{2π}{ω}$$
周期とは、1回転するのにかかる時間のことで、記号T[s]を使います。
物理基礎の波動の分野に登場した周期Tと同じですね。1秒間の回転数のことを振動数fではなく回転数nで表すため、\(n=\frac{1}{T}\)という式が存在しています。
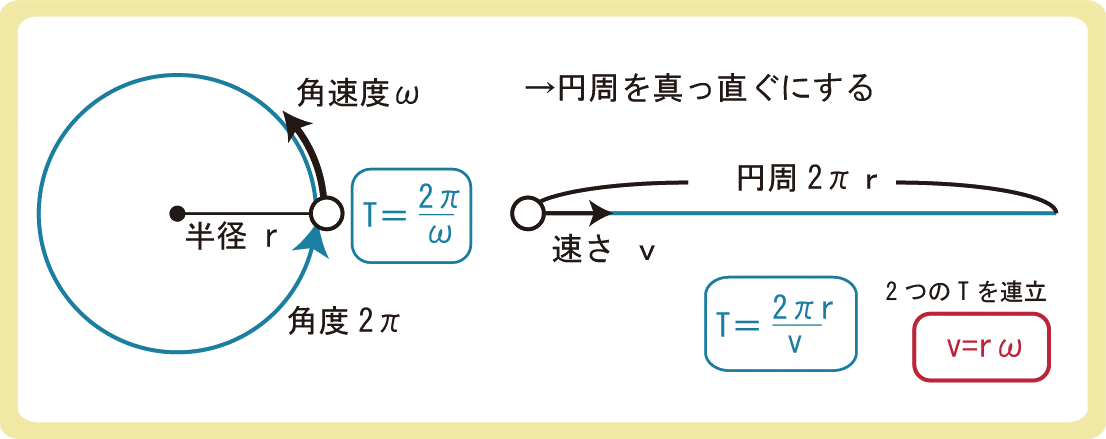
「1回転するのにかかる時間」とは、「1周の角度÷角速度」であると考えられるため、1周の角度2π、角速度ωから\(T=\frac{2π}{ω}\)となります。覚えにくいですが、周期は1周の角度÷角速度と理解していれば思い出しやすいです。
また、半径が\(r\)の円の円周は\(2πr\)であり、円運動の速さを\(v\)とすると、「周期は1周の長さ÷速さ」であるため、\(T=\frac{2πr}{v}\)となります。
今出た2つの公式を連立することで、\(v=rω\)を求めることもできます。
逆に言うと、片方の式と\(v=rω\)さえ覚えていれば、もう片方の式を求めることができます。
例題
例題1
周期10.0秒で等速円運動している物体の角速度は何rad/sか。ただし、円周率π=3.14とする。
まとめ
円運動とは、物体が円形の軌道を描く運動のことであり、円運動の中でも一定の速さで回っている運動のことを等速円運動といいます。
円運動の中でもよく使う式は
$$v=rω$$
$$T=\frac{2πr}{v}\\
T=\frac{2π}{ω}$$
と、次回の内容で解説する向心力についてです。
円運動について、まだ途中までしか解説していないので、向心力を勉強してから問題を解きましょう。