単振り子とは

単振動としてよく登場するもう一つ例が単振り子です。
ばね振り子と比べると登場頻度は少ないですが，大切な内容であることは間違いないため，しっかりと勉強しておきましょう。

それでは，単振り子についてわかりやすく簡単に解説していきます。

単振り子とは

単振り子とは，軽い糸の一端を固定し，他端に小さい物体を取り付け，鉛直面で振動させた振り子のことです。
要は，下図のような振り子のことです。

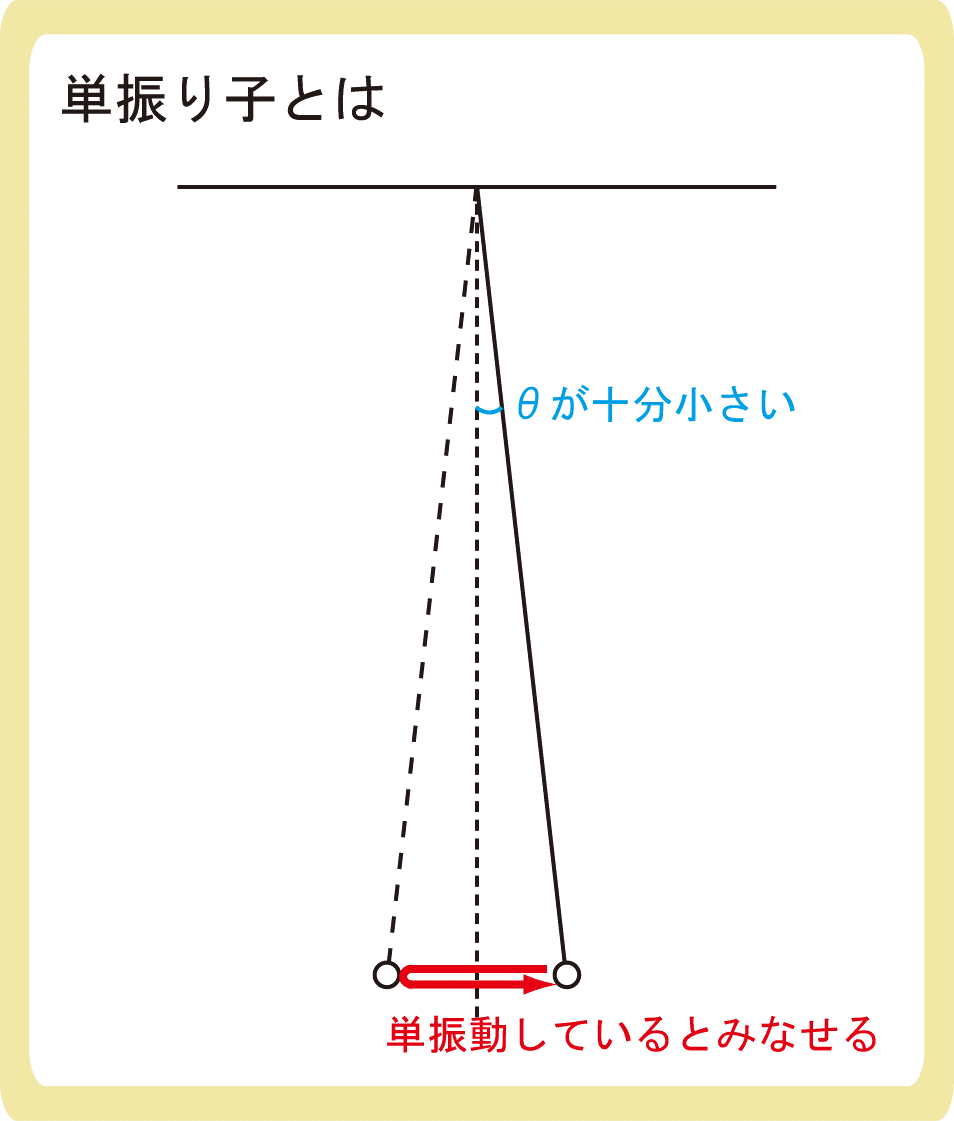
振り子の糸が十分長く物体が十分小さいとき，単振り子は直線を運動しているとみなすことができます。
つまり，振動が十分小さいとき物体は単振動していると考えることができるのです。(振動が大きいと直線上を動いていると言えなくなる)

単振動しているので，物体にはたらく力を図示し，復元力がどうなっているのかを考えましょう。

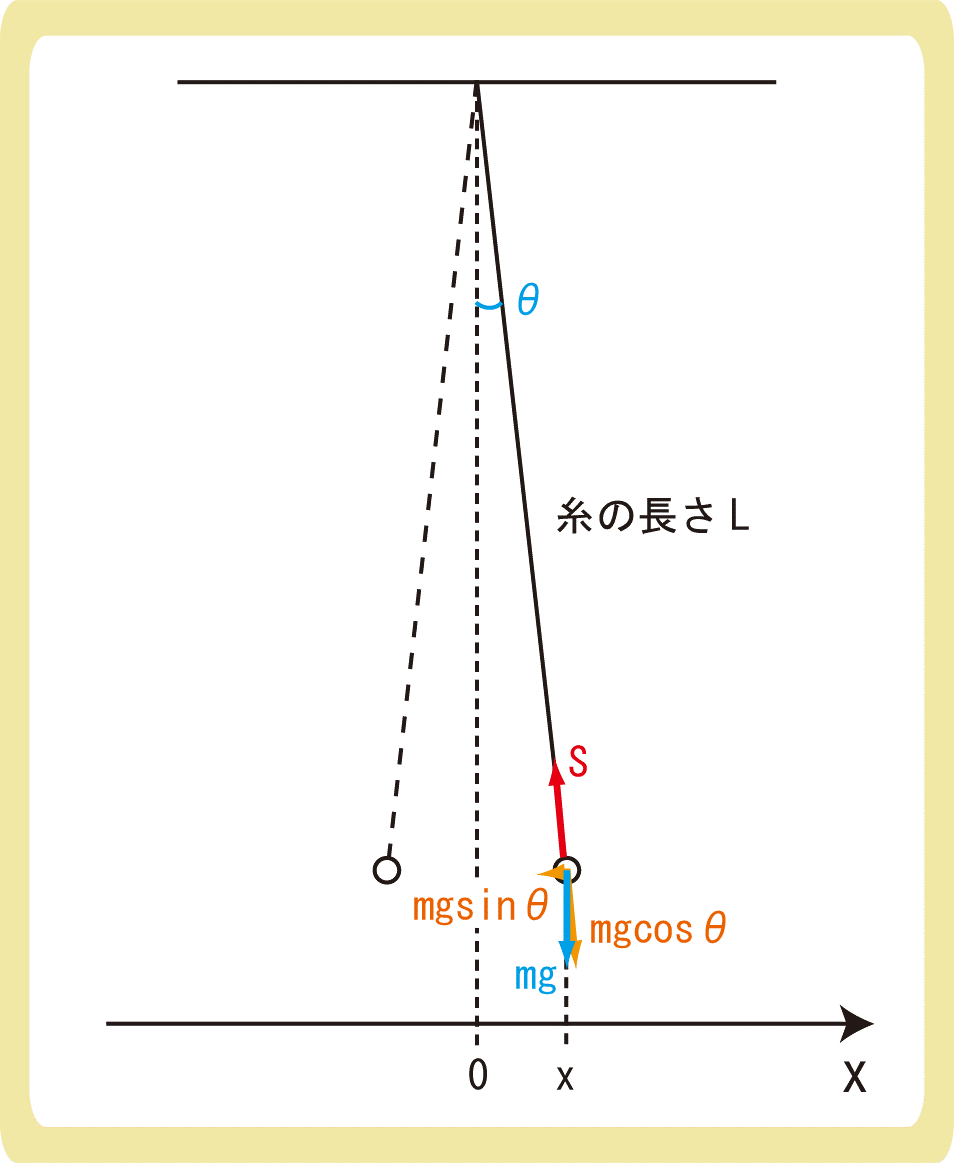
糸の長さをL，物体の質量をmとすると，物体にはたらく力は，上図の重力mgと張力Sの2つです。重力mgを分解すると，mgcosθと張力Sがつり合っていることが分かるため，mgsinθが物体を動かす力であると考えることができます。

上図では力が負の向きなので，

$$F=-mgsinθ$$

となります。

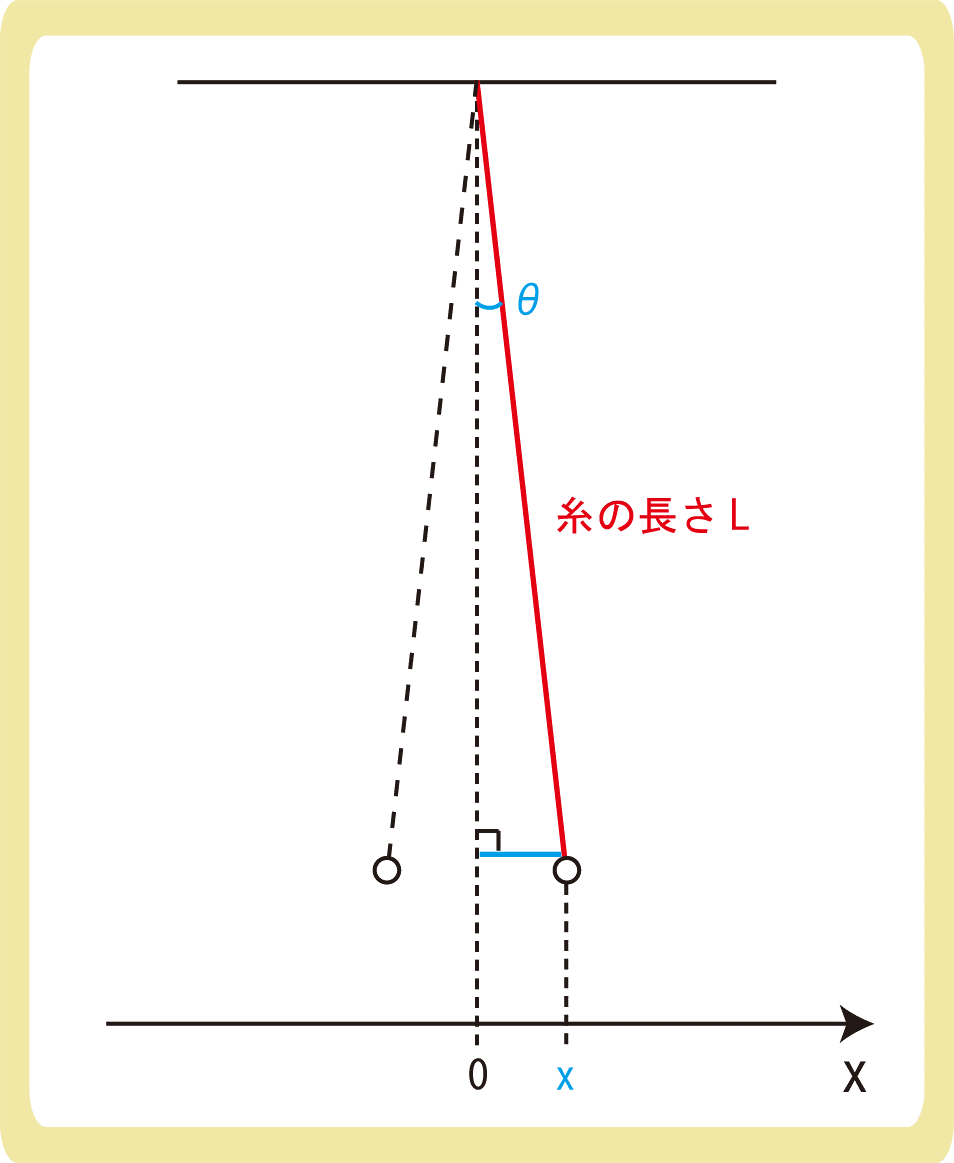
ここで，上図のように糸の長さLと振り子のx成分を考えると，\(sinθ=\frac{x}{L}\)になるので，

$$F=-mgsinθ\\
F=-mg\frac{x}{L}\\
F=-\frac{mg}{L}x\\
F=-Kx$$

となります。つまり，\(F=-\frac{mg}{L}x \)が復元力となるのです。

あとはいつも通り，\(ma=F\)，\(a=-ω^2x\)，\(T= \frac{2π}{ω}\)を使うと，

$$F=-\frac{mg}{L}x\\
ma=-\frac{mg}{L}x\\
-mω^2x=-\frac{mg}{L}x\\
ω=\sqrt{\frac{g}{L}}\\$$

$$T= \frac{2π}{ω}\\
T=2π\sqrt{\frac{L}{g}}$$

となります。
ばね振り子の周期はミカンでしたが，単振り子の周期はリンゴと覚えると簡単です。Lとgなのでリンゴですね。
このように，単振り子の周期は糸の長さLと重力加速度の大きさで決定することを，振り子の等時性といいます。

例題

例題1

糸の長さLの一端を固定し，他端に質量mの物体を付け単振動をさせた。以下の各問に答えなさい。ただし，重力加速度の大きさをgとする。
(1)この単振動の周期を求めなさい。
(2)糸の長さを2Lにしたとき，この単振動の周期は(1)の何倍になるか。
(3)この糸に付ける物体の質量を2mにしたとき，この単振動の周期は(1)の何倍になるか。

まとめ

単振り子とは，振り子を鉛直面で振動させるものです。
糸が十分長く，物体が十分小さいとき，単振り子は単振動をしていると近似することができます。

単振り子の周期は\(T=2π\sqrt{\frac{L}{g}}\)であり，リンゴと覚えておくと楽です。

 

次の内容はこちら

一覧に戻る