ケプラーの法則とは

1600年頃、惑星は太陽の周りを綺麗な円運動をすると考えられていました。ヨハネス・ケプラーは師であるティコ・ブラーエが21年間観測した（なんと、肉眼で観測した！）膨大な観測データを、ティコ・ブラーエの死後に整理・解析をしました。
主に地球と火星のデータを解析したのですが、何度計算しても地球と火星の距離の計算が合わず、惑星は楕円運動をしているという仮説を立てることになりました。そこから、ケプラーの法則と言われる3つの法則が発表されたのです。

今回は、ケプラーの法則とは何かについて、わかりやすく簡単に解説していきます。

ケプラーの法則とは

ケプラーの法則とは、ケプラーが提唱した惑星の運動に関する法則です。
一つ一つ、どのような法則なのかを見ていきましょう。

ケプラーの第1法則とは

ケプラーの第1法則とは、惑星は太陽を焦点とする楕円軌道を取るという法則です。
要は、地球は太陽の周りをきれいな円軌道を取っているのではなく、楕円として公転しているのです。

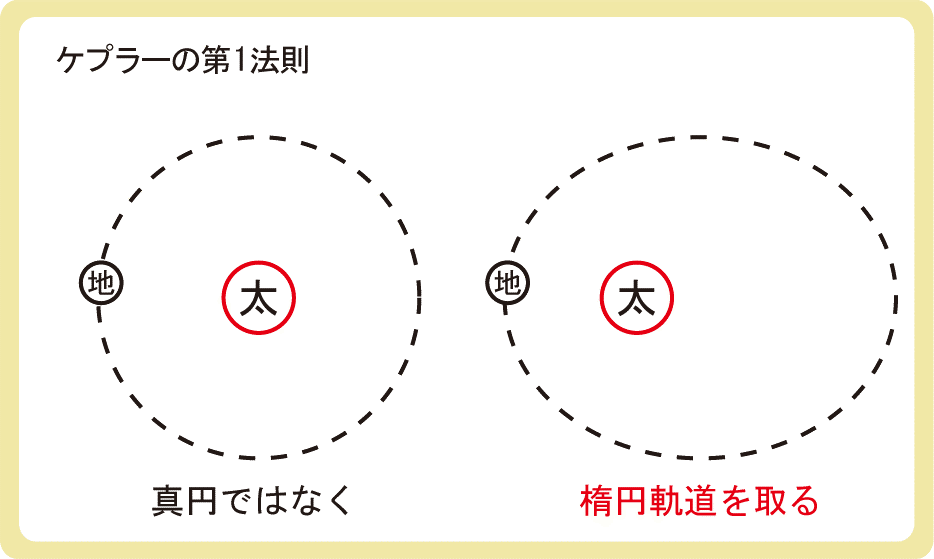
楕円といっても真円に近い楕円であるため、高校物理では惑星は円軌道を取るものとして考える場合が多いです。楕円軌道を取ることが天動説を覆す鍵となるのですが、高校物理ではあまり気にしなくていい内容かもしれませんね。

ケプラーの第2法則とは

ケプラーの第2法則とは、惑星と太陽の線分が単位時間に描く面積は一定であるという法則のことであり、面積速度一定の法則ともいいます。

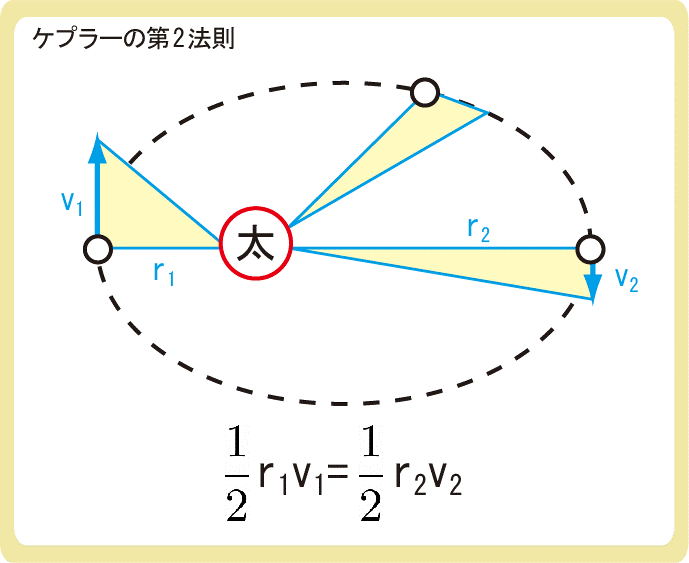
惑星と太陽の線分の描く面積が一定になるというのは、上図の黄色い部分の面積が常に一定になるように惑星の速度が変化することであり、
簡単にいうと太陽に近ければ速く、遠ければ遅くなるという法則です。
面積は上図のような三角形になるため、\(\frac{1}{2}r_1v_1=\frac{1}{2}r_2v_2\)と表せます。

実は、惑星でなくても力が一点に向っている運動では面積速度一定の法則が成り立ちます。もしかしたら、振り子や電磁気力の問題で使うかもしれません。
基本問題にはあまり登場してきませんが、応用問題になると見かけることが多いため、\(\frac{1}{2}r_1v_1=\frac{1}{2}r_2v_2\)という式を今ここで覚えておきましょう。

ケプラーの第3法則とは

ケプラーの第3法則とは、惑星の公転周期Tの2乗と半長軸aの3乗の比は一定であるという法則です。

$$\frac{a^3}{T^2}=k$$

長軸・短軸とは

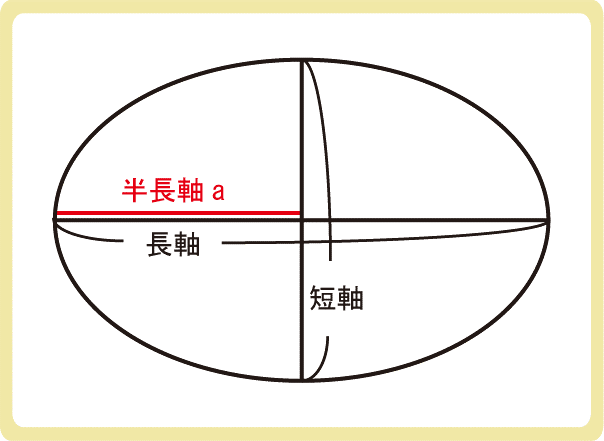
楕円には焦点が2つあります。2つの焦点を通る直線を楕円の内部に引いたものを長軸、その垂直二等分線を楕円の内部に引いたものを短軸といいます。
簡単にいうと、楕円の最も長い直径が長軸、最も短い直径が短軸です。
半長軸とは長軸の半分のことで、記号aを使います。ここら辺は数学で勉強する内容ですね。

ケプラーの第3法則とは

公転周期とは太陽の周りを1周するのにかかる時間のことで、地球なら1年です。これをTと置きます。このとき、\(\frac{a^3}{T^2}\)はどの惑星でも一定となるという法則がケプラーの第3法則です。
\(\frac{a^3}{T^2}\)が一定なので、\(\frac{a^3}{T^2}=k\)とする場合が多いです。なお、kは定数なので、aとTのどちらが分母分子が逆でも良いです。

例えば、地球と太陽の間の距離は1天文単位であり、公転周期は1年なので、

$$\frac{a^3}{T^2}=\frac{1^3}{1^2}\\
\frac{a^3}{T^2}=1$$

となります。

火星と太陽の間の距離は約1.52天文単位、公転周期は1.88年なので、

$$\frac{a^3}{T^2}=\frac{1.52^3}{1.88^2}\\
\frac{a^3}{T^2}=0.9936…$$

つまり、約1ですよね。
水星でも木星でも天王星でも、\(\frac{a^3}{T^2}\)を計算してみて下さい。全部約1になります。

私は、大文字のAは3画なので3乗、Tは2画なので2乗と暗記していました。

例題

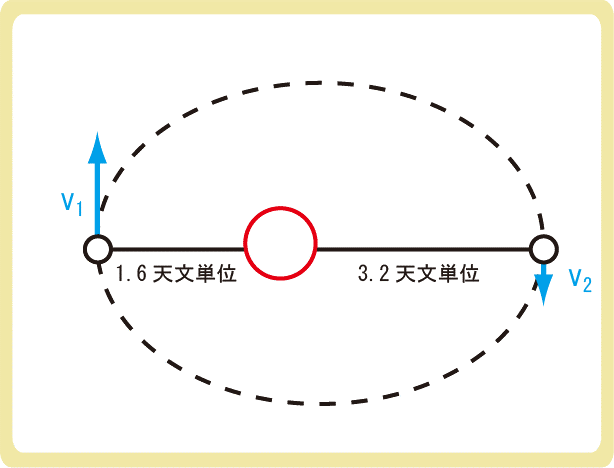
例題1

下図のように恒星の周りを惑星が運動しているとき、v₁はv₂の何倍であるか求めなさい。

まとめ

ケプラーの法則とは、ケプラーが提唱した惑星の運動に関する法則です。
その中でも、ケプラーの第2法則は\(\frac{1}{2}r_1v_1=\frac{1}{2}r_2v_2\)という式で表され、面積速度一定の法則ともいいます。
ケプラーの第3法則は\(\frac{a^3}{T^2}=k\)という式で、稀に登場してきます。

 

次の内容はこちら

一覧に戻る