万有引力の法則とは

「リンゴは落ちるのになぜ月は落ちないのか」という疑問から力学を導いた逸話が有名なニュートンは、地球上での法則とケプラーの残した宇宙に関する法則を1つにまとめました。それが万有引力の法則です。

万有引力の法則とは一体どのような内容なのか、わかりやすく簡単に解説していきます。

万有引力の法則とは

万有引力の法則とは、すべての質量をもつ物体は互いに引き合っているという法則です。
あなたとスマホ、天井と床、地球とボール、ありとあらゆる物体がお互いに引っ張り合っていると考えます。

万有引力は引き合う2つの物体の質量に比例し距離の2乗に反比例します。

$$F=G\frac{m_1m_2}{r^2}$$

Gは万有引力定数という定数であり、値はG=6.67×10^-11 (N・m²/kg²)です。

万有引力定数は10^-11と非常に小さいため、万有引力は小さな力となり通常は無視できるのですが、地球や太陽規模の大きさになると無視できない値になります。

例題1

質量60kgの人と質量80kgの人が4.0m離れているとき、この2人の間にはたらく万有引力の大きさは何Nか。ただし、万有引力定数を6.67×10^-11 (N・m²)/kg²とする。

万有引力の法則と重力

万有引力はとても小さな力ですが、地球くらい大きな質量の物体について考えると無視できない大きさになります。

その典型的な例が重力です。重力は地球と物体間にはたらく万有引力というわけです。

地球の重心（中心にあるとする）と地球上にある物体間にはたらく万有引力の大きさを計算するとみんなもよく知っているあの数値が出てきます。

例題2

地球上に置いた質量1.00kgの物体にはたらく万有引力の大きさを求めよ。ただし、地球の質量Mを5.97×10²⁴kg、地球の半径Rを6.37×10⁶m、万有引力定数を6.67×10^-11 (N・m²)/kg²とする。

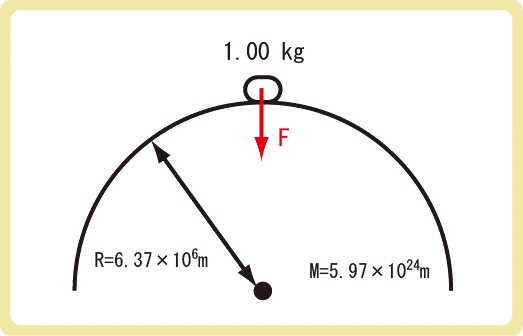
万有引力の法則と重力

例題2の解答をみて下さい。
重力mgより、1.0kgの物体にはたらく力の大きさは9.8Nであるということを私たちは知っています。
上の例題2の結果は、重力が万有引力であることを計算で確かめたことになります。地球上では万有引力F＝mgであるということです。

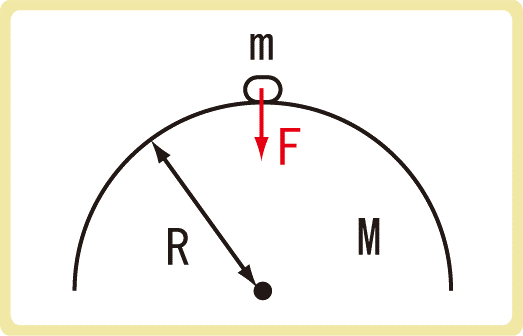
例題2を数値ではなく文字だけで考えてみましょう。
万有引力の範囲では、地球の質量をM、地球の半径をRとします。

万有引力の法則の公式より、地球上ではF=mgであることを利用すると、

$$F=G\frac{m_1m_2}{r^2}\\
mg=G\frac{Mm}{R^2}\\
g= G\frac{M}{R^2}\\
gR^2=GM$$

となります。
この式は万有引力定数Gが問題文にないときに使います。

重力＝万有引力と覚えておくと公式を導くことができるので、公式を覚えるよりも、\(mg=G\frac{Mm}{R^2}\)となることを理解しておきましょう。

まとめ

万有引力とは、全ての物体と物体の間にはたらく引力のことです。公式は\(F=G\frac{m_1m_2}{r^2}\)であり、とても小さい値なので基本的に無視できるのですが、地球規模の大きさの物体であると無視できない大きさになります。

重力は万有引力の1つであり、地球と私たちの間にはたらく万有引力を重力と呼んでいます。
地球上では\(mg=G\frac{Mm}{R^2}\)であることから、\(gR^2=GM\)という式を導くことができます。問題文に万有引力定数Gがないときに使うので、必ず知っておきましょう。

次の内容はこちら

一覧に戻る