・定積変化とは
・定圧変化とは
今回は，定積変化と定圧変化についてわかりやすく簡単に解説していきます。よろしくお願いいたします。
定積変化とは
気体の体積を一定にしたまま温度や圧力を変化させること
定積変化では\(W=0\)となる
定積変化とは，気体の圧力を一定にしたまま温度や圧力を変化させることです。
気体の体積が一定ということは，膨張もせず圧縮もしないということなので仕事をしません。定積変化はこれが全てです。
大事なのでもう一度言うと，気体が膨らまない(縮まない)ということは仕事をしない，つまりW=0 Jということです。「定積変化，体積一定だからW=0」と理解しておきましょう。
ここで，p-Vグラフについて説明します。
縦軸が圧力p，横軸が体積Vのグラフのことをp-Vグラフといいます。気体の状態変化ではp-Vグラフが分かるかどうかが非常に重要です。
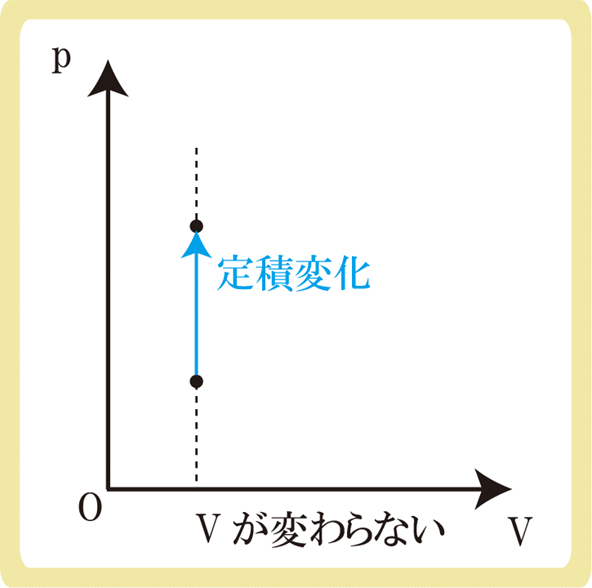
p-Vグラフにおいて，定積変化ではグラフが上下に変化します。
体積が一定なので左右には動かず，上下のみ移動することになります。p-Vグラフでは右上にいくほど温度が高くなるので，上に変化しているときは温度が上昇します。
定圧変化とは
気体の圧力を一定にしたまま温度や体積を変化させること
定圧変化では\(W=-pΔV\)となる
定圧変化とは，気体の圧力を一定にしたまま温度や体積を変化させることです。
定圧変化の特徴は”圧力が一定であること”です。
”気体を膨らませる(縮める)ときの力が一定”なので，仕事W’=FΔxを使うことができます。
力学で登場したW’=FΔx のW’は，した仕事であるため，WではなくW’にしています。また，力が一定でない場合，万有引力による位置エネルギーのように積分をする必要がでてくるため，力が一定の場合のみW’=FΔxを使うことができます。
ここで，\(F=pS\)，\(V=S×x\)(体積=底面積×高さ)をW’=FΔxに代入すると，
$$W’=FΔx\\
W’=pS×\frac{ΔV}{S}\\
W’=pΔV\\
W=-pΔV$$
となります。
「Wは”された仕事”，圧縮しているときがプラス」になり，「ΔVは体積の増加，膨張したときがプラス」になるため，公式にマイナスが登場してくるんだという直感的な理解でも構いません。
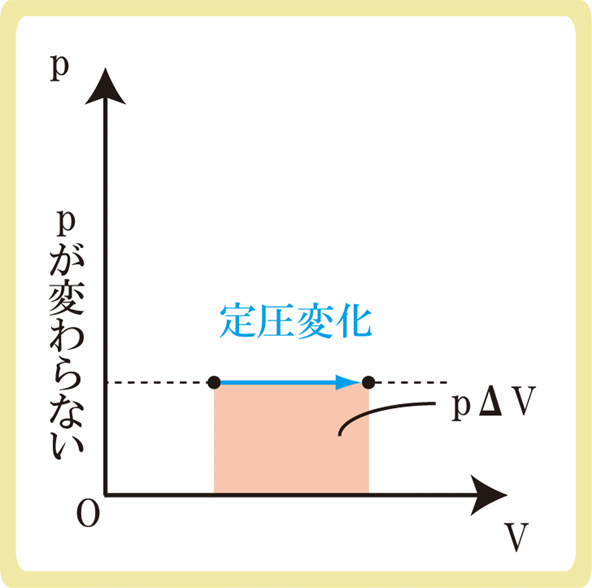
p-Vグラフにおいて，定圧変化ではグラフが左右に変化します。圧力が一定なので上下には動けないため，左右のみ変化することになります。
また，p-Vグラフでは右上にいくほど温度が高くなるので，右に変化しているときは温度が上昇しています。
定圧変化の作る面積の大きさがpΔVの大きさと等しいため，公式を覚えなくてもグラフの面積から仕事を求めることができます。
気体が膨張しているときは気体がした仕事Wはマイナス，気体が圧縮されているときは気体がされたWはプラスです。
例題
例題1
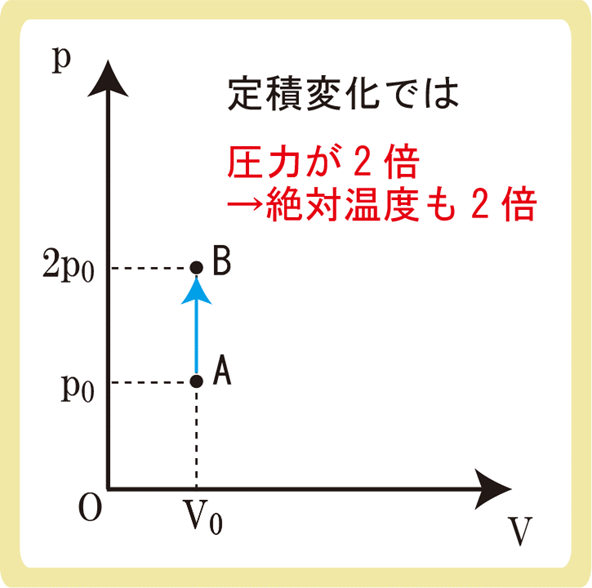
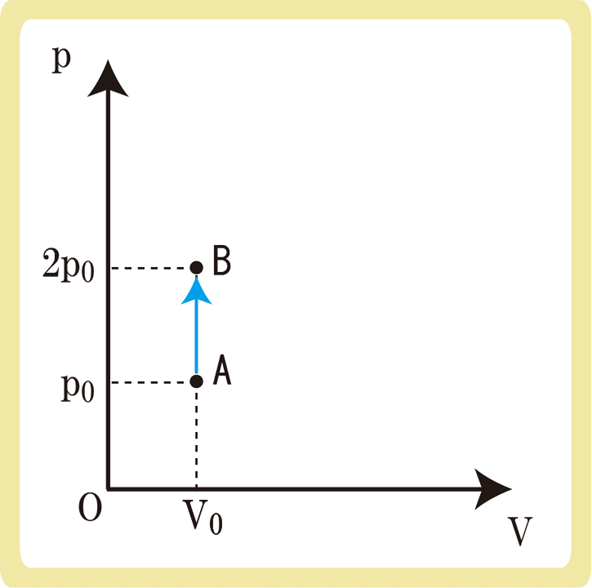
下図のように，物質量が一定の理想気体をA→Bと状態変化させた。Aの絶対温度をT0とするとき，次の各問に答えなさい。
(1)Bの絶対温度を求めなさい。
(2)気体がされた仕事Wを求めなさい。
気体の状態変化では
・単原子分子理想気体かどうか
・①定積変化 ②定圧変化 ③等温変化 ④断熱変化 のうちどれなのか
を，まず確認します。
今回は単原子分子理想気体ではないため，\(U=\frac{3}{2}nRT\)は使いません。
また，p-Vグラフが上下に移動する変化は定積変化であるため，定積変化\(W=0\)を使うと考えましょう。
(1) 物質量をn，気体定数をR，Bでの絶対温度をTBとするとき，
理想気体の状態方程式より，AとBにおいて
$$p_0V_o=nRT_0$$
$$2p_0V_0=nRT_B$$
と式を作ることができます。
上の式を見比べると，明らかに\(T_B=2T_0\)となります。
簡単に言うと，定積変化では圧力が2倍になると絶対温度も2倍になるのです。
∴2T0
(2)定積変化では気体の体積が変わらないため\(W=0\)です。
∴0 J
例題2
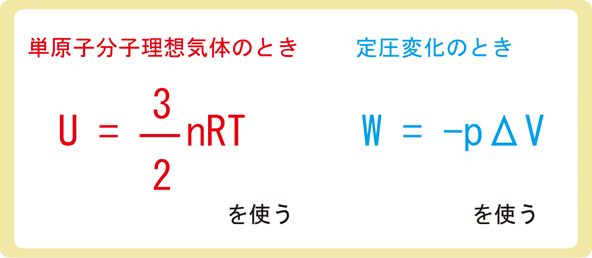
下図のように，物質量がnである単原子分子理想気体がなめらかに動くピストンの付いている容器の中に入っている。この気体に熱を与えたところ，気体が膨張し，温度がΔTだけ上昇した。以下の各問に答えなさい。ただし，気体定数をRとする。
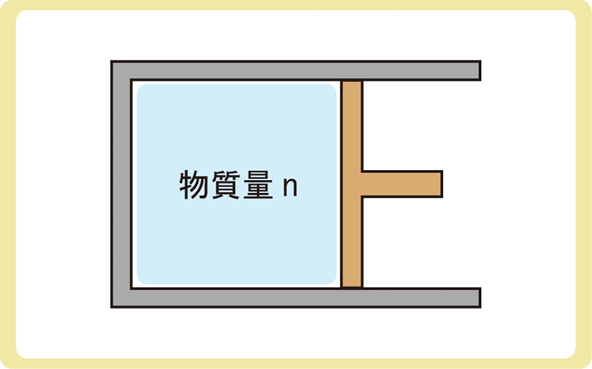
(1)気体がした仕事W‘を求めよ。
(2)気体の内部エネルギーの変化ΔUを求めよ。
(3)気体に与えた熱量Qを求めよ。
気体の状態変化では
・単原子分子理想気体かどうか
・①定積変化 ②定圧変化 ③等温変化 ④断熱変化 のうちどれなのか
を，まず確認します。
今回は単原子分子理想気体であるため\(U=\frac{3}{2}nRT\)を使うと考えましょう。
また，ピストンがなめらかに動くとき，ピストンは力がつり合ったまま動くと考えるため，圧力が一定，つまり定圧変化であると考えることができます。
(・気体が膨張している→定積ではない
・温度が上昇→等温変化ではない
・熱を与えている→断熱変化ではない
と考えることもできます。)
単原子分子理想気体なので\(U=\frac{3}{2}nRT\)，今回は物質量が一定であるため\(ΔU=\frac{3}{2}nRΔT\)を使うことができます。
また，定圧変化では\(W=-pΔV\)となるため，定圧変化のときはこの公式を使うと考えましょう。
(1) \(W=-pΔV\)のWは”気体がされた仕事”であるため，”気体がした仕事”を求めるために，符号を変えた\(W’=pΔV\)を使いましょう。
また，pとVは問題に登場していないため，答えとして使ってはいけません。
定圧変化かつ物質量が一定のとき\(pΔV=nRΔT\)を使うことができるため，答えは\(nRΔT\)としましょう。
$$W’=pΔV\\
W’=nRΔT$$
∴\(nRΔT \)
(2) 単原子分子理想気体かつ物質量が一定のとき，\(ΔU=\frac{3}{2}nRΔT\)です。
∴\(\frac{3}{2}nRΔT\)
(3)熱力学第一法則\(ΔU=Q+W\)を使うことで，気体に与えた熱量Qを求めることができます。
$$ΔU=Q+W\\
\frac{3}{2}nRΔT=Q- nRΔT\\
Q=\frac{5}{2}nRΔT$$
∴\(\frac{5}{2}nRΔT\)
まとめ
定積変化は「体積が一定」の変化で，p-Vグラフでは上下に動き，\(W=0\)
定圧変化は「圧力が一定」の変化で，p-Vグラフでは左右に動き，\(W=-pΔV\)です。気体がされた仕事Wは，p-Vグラフの面積から求めることもできます。
