皆さんは秘書問題をご存知でしょうか?
行動の指針になるような面白い話ですので、知っているだけでより良い選択ができるようになるかもしれません。
今回は、秘書問題について解説していきます。
秘書問題とは
- 秘書を1人雇いたいとする。
- \(n\)人が応募してきている。\(n\)という人数は既知である。
- 応募者には順位が付けられ、複数の応募者が同じ順位になることはない(1位からn位まで重複無く順位付けできる)。
- 無作為な順序で1人ずつ面接を行う。次に誰を面接するかは常に同じ確率である。
- 毎回の面接後、その応募者を採用するか否かを即座に決定する。
- その応募者を採用するか否かは、それまで面接した応募者の相対的順位にのみ基づいて決定する。
- 不採用にした応募者を後から採用することはできない。
このような状況で、最良の応募者を選択することが問題の目的である。
秘書問題(Wikipediaより引用)
上記のような問題を秘書問題と呼びます。
めっちゃ簡単に説明すると、
- 秘書を1人雇いたい
- 一人ずつ順番に面接し、その場で採用か不採用か決める
- 「この人だ!」と一人採用したら終了
- 採用した後、残りの人とは面接しない
- 不採用になった人ともう一度面接し、採用することはできない
一番良い人を採用するためにはどうすればいい?
ということですね。




最後の人が一番良い人である確率って、低そうですよね
秘書問題の答え
秘書問題は数学的に解が求められています。
- まず、最初の37%の人は不採用にする
- 最初の37%の人の中で一番良い人を覚えておく
- それ以降の人の中で、最初の37%の中で最も優秀だった人を上回った人が現れたら採用する
そうすると、約37%の確率で一番良い人を採用できる
これが秘書問題の答えです。
もし、100人の応募者から秘書を選ぶとしたら、最初の37人は必ず不合格にし、38人目以降の中で最初の37人より良い人を見つけたら採用する。
という戦略を取れば良いと分かっています。
秘書問題の他にも最適停止問題と呼んだり、何人目の恋人と結婚すれば良いのかと例えることから結婚問題と呼んだりもします。
なお、秘書問題では「応募してきた全体の人数が分かること」と「応募が十分に大きいこと」が前提になるので、人生で何人と付き合う(関係をもつ)か分からない or 付き合う人数が少ない場合は効果が薄くなります。
結婚・婚活で秘書問題の答えを使おうとしている人は、上記の点に注意をしてくださいね。
もちろん、時が経てば人は変わるものなので、前ダメだった人が未来では一番良くなっているかもしれません。
ちなみに、約37%という数字は、ネイピア数\(e\)の逆数です。
$$\frac{1}{e}≒0.37$$
数学が好きな人は、答えがネイピア数や円周率になったり、簡単に表せたりすると「美しい!!!」と言うので、答えがネイピア数の逆数になるということで有名な問題でもあります。
秘書問題をわかりやすく簡単に数学的に計算し証明
少し難しいですが、可能な限り秘書問題をわかりやすく簡単に説明したいと思います。
もちろん数学なので、計算をし証明することになります。
高校の数学Ⅲレベルの知識があれば十分に理解することが可能です。
—-証明—-
応募者の人数を\(n\)人とすると、\(t\)番目の人が最も優秀な人である確率は単純に$$\frac{1}{n}$$です。
このとき、\(n\)人中、\(k\)人目までは無条件で不合格とします。
(もちろん、\(n>k\)です。)
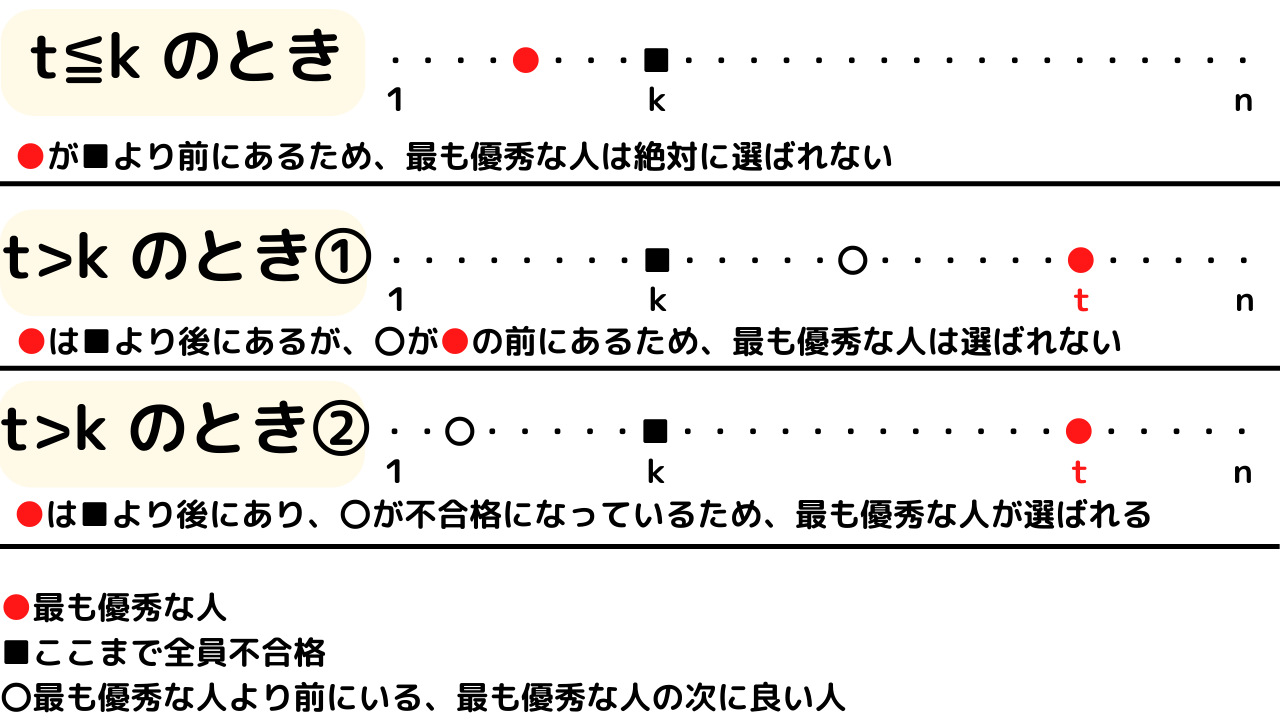

\(t≦k\)のとき、最も優秀な人は無条件で不合格となってしまっているため、最も優秀な人が選ばれる確率は\(0\)です。
\(t>k\)のとき、最も優秀な人は不合格となっていないため、選ばれる確率があります。
ただ、もし最も優秀な人の直前に、次に優秀な人がいれば、次に優秀な人が選ばれてしまい、最も優秀な人は選ばれなくなってしまいます。
つまり、最も優秀な人の次に優秀な人が、不合格となった人の後~最も優秀な人より前にいる場合、最も優秀な人は選ばれません。(上の画像の①にあたる)
一方、最も優秀な人の次に優秀な人が不合格となっていた場合、最も優秀な人が選ばれるため、上記の画像でいうところの②の場合だけ考えれば良いことになります。
(最も優秀な人の次に優秀な人ではなく、tより前にいる人の中で一番優秀な人がより正しい表現)
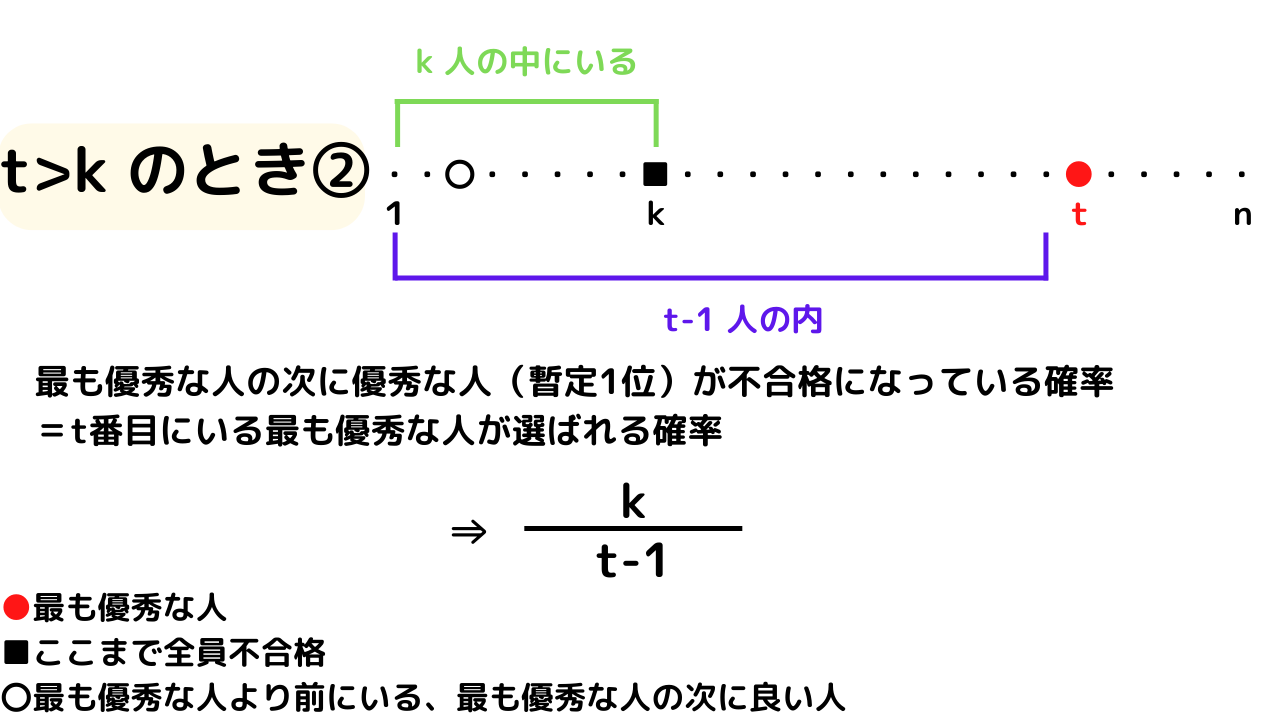

\(t>k\)のとき②の確率は、\(t-1\)人の中で、\(1\)~\(k\)番目の間に、次に優秀な人がいれ良いと考えればいいので、$$\frac{k}{t-1}$$となります。
\(t\)番目の人が最も優秀な人がいる確率\(\frac{1}{n}\)を合わせて考えると、最も優秀な人が選ばれる可能性\(P(k)\)は
$$P(k)=\frac{1}{n}\displaystyle \sum_{i=k+1}^{n}\frac{k}{t-1}$$
となるので、後はこれを計算していきます。
$$P(k)=\frac{1}{n}\displaystyle \sum_{i=k+1}^{n}\frac{k}{t-1}\\
P(k)=\frac{k}{n}(\frac{1}{k}+\frac{1}{k+1}+・・・+\frac{1}{n-1})$$
となり、\(n\)が十分大きいとき、
$$\frac{1}{k}+\frac{1}{k+1}+・・・+\frac{1}{n-1}≒log\frac{n}{k}$$
であるため、
$$P(k)=\frac{k}{n}log\frac{n}{k}$$
であると考えます。
ここで、
$$P(k)=\frac{k}{n}log\frac{n}{k}$$
のグラフの概形は下の図のような上に凸なグラフになるため、\(P(k)\)を\(k\)で微分し、\(P'(k)=0\)のときの値を求め、代入することで\(P(k)\)最大値を求めることができます。
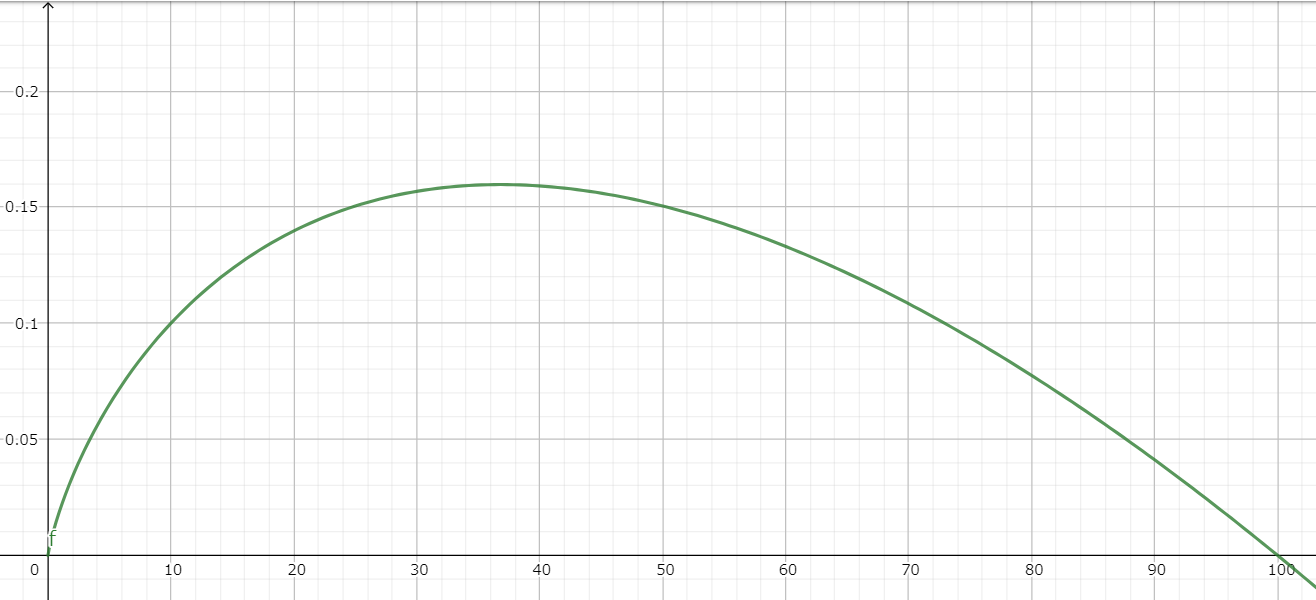

※\(n=100\)のときのグラフの概形
\(P(k)\)を\(k\)で微分すると(合成関数の微分)、
$$P'(k)=\frac{1}{n}log\frac{n}{k}-\frac{1}{n}$$
\(P'(k)=0\)のときを考えれば良いので、
$$\begin{eqnarray}0&=&\frac{1}{n}log\frac{n}{k}-\frac{1}{n}\\
\\
\frac{1}{n}log\frac{n}{k}&=&\frac{1}{n}\\
\\
log\frac{n}{k}&=&1\\
\\
\frac{n}{k}&=&e\\
\\
k&=&\frac{n}{e}\end{eqnarray}$$
となります。
(\(e\)はネイピア数)
この\(k\)を\(P(k)\)に代入すると、
$$\begin{eqnarray}P(k)&=&\frac{k}{n}log\frac{n}{k}\\
\\
&=&\frac{\frac{n}{e}}{n}log\frac{n}{\frac{n}{e}}\\
\\
&=&\frac{1}{e}loge\\
\\
&=&\frac{1}{e}\\
\\
&≒&\frac{1}{2.71828・・・}\\
\\
&≒&0.3678・・・\\
\\
&≒&37%
\end{eqnarray}$$
となります。
—-証明終了—-
つまり、この戦略を使えば、約37%の確率で最も優秀な人を採用できるのです。
順位最小化問題 秘書問題の応用
正直、37%で一番優秀な人を採用できると言われても確率的に微妙ですよね。
一位じゃなくて二位でも良いということで、「可能な限り順位の高い人を採用したい!」と考えることを順位最小化問題と言います。
順位最小化問題の結論は以下の通りです。
- 最初の26%人を不合格とし、その後の人で一番良い人がいれば採用
- 合計45%人まで現れなかったら、2位以内であれば採用
- 56%人まで現れなかったら、今までの中で3位以内なら採用
という戦略を取ることで、平均して約3.87位の人を採用することができます。
ちなみに、64%で4位、70%で5位、74%で6位、77%で7位・・・と続いていきます。
$$t_s=\displaystyle \prod_{j=s}^∞ (\frac{j+2}{j})^{-\frac{1}{j+1}}\\
\\
(※ s=1, 2, 3…)$$
この式に代入すれば計算することができます。一応解説しますが、
3位以内(56%)は、上記の式の\(j\)に\(3\)を代入したもの × \(j\)に\(4\)を代入したもの × \(j\)に\(5\)を代入したもの × … と計算。
7位以内(77%)を求める方法は、上記の式の\(j\)に\(7\)を代入したもの × \(j\)に\(8\)を代入したもの × \(j\)に\(9\)を代入したもの × … と計算します。
この戦略を取れば平均して約3.87位の人を採用できるのですから、かなり運が悪くない限り良い人を選べると思います。
まとめ
最初の37%は不合格、それ以降で一番の人を探す!
以上が秘書問題に関する解説になります!
秘書問題も順位最小化問題も最初の37%や26%を基準とするので、最後まで確認せずとも前半の内容である程度判断をするのが良いのではないでしょうか。
数学って難しいですね。












